ОПРЕДЕЛЕНИЕ ГРУППЫ. ЭКВИВАЛЕНТНОСТЬ ДВУХ ОПРЕДЕЛЕНИЙ ГРУПП.
БИНАРНАЯ АЛГЕБРАИЧЕСКАЯ ОПЕРАЦИЯ (БАО). СВОЙСТВА.
Пусть дано не пустое множество А.
Определение.
Говорят, что на множестве А выполнима бинарная алгебраическая операция (*), "а,bÎА, одинаковым или различным взятым в определенном порядке по некоторому правилу или закону ставится в соответствие определенный единственный элемент сÎА.
(А,*) *: +, -, ⋅, /, ⋂, ⋃. a*b=c, c-композиция элементов a и b.
Требование к БАО:
1. Выполнимость, элемент сÎА;
2. Однозначность, с – единственное(!);
Рассмотрим прямое произведение множества А на себя А*А=А², оно состоит из всевозможных упорядоченных пар элементов из А. Оно состоит из всевозможных упорядоченных пар элементов из А.
Определение.
Всякое отображение множества А² на или в множество А называется БАО на множестве А.
Наряду с бинарными алгебраическими операциями рассматривается также:
1. Нульарная операция – это правило или закон по которому выделяются особые элементы из множества А.
2. Унарная операция – по этой операции любому элементу из А ставится в соответствие единственный элемент из этого множества.
Пример, дано z, "аÎZ, а ® -а, элементу а соответствует противоположный элемент -а, где -аÎZ.
Q; (Q,⋅), "аÎQ, а ® 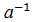 ,
, 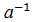 ÎQ. Взятие обратного элемента не является унарной операцией на Q, так как нулю нет обратного элемента.
ÎQ. Взятие обратного элемента не является унарной операцией на Q, так как нулю нет обратного элемента.
3. Тернарная операция – это любой упорядоченной тройке элементов из А ставится в соответствие единственный элемент из А.
|
|
|
Пример, (Z,*); * - нахождение НОД, a,b,cÎZ, и так далее.
n-арная операция – это любой упорядоченной n-ке элементов из А, ставится в соответствие единственный элемент из множества А.
Если дана n-арная операция, то n называют рангом этой операции.
Пример, выяснить являются ли БАО следующие операции на множестве.
1.(М,+), М – множество квадратичных матриц n-го порядка с действительными коэффициентами, да являются.
2.(М,∙), "А,ВÎМ, |А|≠0, |В|≠0, |А⋅В|=|А|⋅|В|≠0, А⋅ВÎМ, определитель произведения двух матриц равен произведению их определителей(Является БАО).
Рассмотрим свойства БАО.
Обозначим через А множество векторов трехмерного векторного пространства, зададим на этом множестве операцию звездочку (*), а звездочка (*) скалярное произведение векторов, так как результатом скалярного произведения двух векторов является число.
Свойства БАО:
1. БАО (*) заданная на множестве А называется коммутативной: "a,bÎА, a*b=b*a, (Z,-): a-b≠b-a;
2. БАО (*) заданная на множестве А называется ассоциативной: "a,b,cÎА, a*(b*c)=(a*b)*c;
Пример 1. (Z,+), Z - множество целых чисел, ассоциативно, т.е a+(b+c)=(a+b)+c;
Пример 2.( Z,-), a-(b-c)≠(a-b)-c;
Пусть на ряду с БАО * на множестве А задана БАО нулик(◦).
|
|
|
3. БАО * называется дистрибутивной относительно операции нулик, если " a,b,cÎА, a*(b◦c)=(a*b)◦(a*c);
Пример 3. (Z,⋅,+),"A,B,CÎZ, a⋅(b+c)=a⋅b+a⋅c;
(Z,+,⋅),"a,b,cÎZ, a+(b⋅c)≠(a+b)⋅(a+c);
(J,⋃,⋂), "A,B,CÎ J, A⋂(B⋃C)=(A⋂B)⋃(A⋂C);
Элемент еÎА называется нейтральным элементом относительно операции (*), если "аÎА, а*е = е*а = а:
a) Если операция (*)=+, то е=0 - нулевой элемент;
b) Если операция (*)= ∙, то е=1 - единичный элемент;
4. Элемент а′ÎА называется симметричным для элемента аÎА, относительно операции звездочка(*), если выполняется равенство:
а′ * а = а * а′ = е,
*:-,+; а′=-а - противоположный элемент; *:-,⋅; а′= 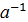 -обратный элемент.
-обратный элемент.
Пусть дано (А;*) говорят, что на множестве А выполнима обратная операция для операции *, если для "a,bÎА уравнения a*x=b и y*a=b имеют одинаковое решение.
Замечание. Если *-коммутативно, то x=y достаточно рассматривать "их этих уравнений.
Если *=+, то a+x=b, y+a=b (обратная операция вычитание), а когда *= ⋅, то a⋅x=b, y⋅a=b (обратная операция деление).
АЛГЕБРА. ВИДЫ АЛГЕБР.
Пусть дано не пустое множество А на котором задана система алгебраических операций.
Определение. Множество, алгебраических операций на котором задана одна или несколько алгебраических операций называется алгеброй. Иначе алгебра это множество, на котором задана система алгебраических операций.
|
|
|
Упорядоченная совокупность рангов заданных операций называют типом алгебры. И говорят: две алгебры имеющие одинаковый тип называются однотипными. Алгебра (В, W) называется подалгеброй для алгебры (А, W), если ВÌА.
В зависимости от числа операций, видов и их свойств выделяют различные алгебры, например: группоиды, полугруппы, группы, кольца, поля линейные пространства и т.д.).
Множество на котором задана одна алгебраическая операция называется группоидом.
Множество на котором задана одна бинарная ассоциативная алгебраическая операция называется полугруппой.
Множество на котором задана одна бинарная ассоциативная алгебраическая операция и есть нейтральный элемент называется моноидом. Одним из важнейших примеров алгебр являются группы.
ОПРЕДЕЛЕНИЕ ГРУППЫ. ЭКВИВАЛЕНТНОСТЬ ДВУХ ОПРЕДЕЛЕНИЙ ГРУПП.
I. Не пустое множество G≠Æ называется группой G, если в нем определена одна бинарная алгебраическая операция G * удовлетворяющая следующим аксиомам:
|
|
|
1. (*-ассоциативна)" a, b, cÎG, a*(b*c)=(a*b)*c;
2. $ нейтральный элемент относительно операции *,$еÎG, "aÎG, a*e=e*a=a;
3. Для " элемента из G существует ему симметричный "aÎG, $a¢ÎG, a*a¢=a¢*a=e;
II. Не пустое множество G называется группой, если в нем определена одна бинарная алгебраическая операция * удовлетворяющая двум аксиомам:
1. Операция * - ассоциативна;
2. В G выполнима обратная операция для операции *: "a,bÎG, a*x=b, y*a=b имеют единственное (!) решение;
Если операция * коммутативна, то группу G называют абелевой.
Если операция *:+,-, то группа G называется аддитивной.
Если операция *: ∙, то группа G называется мультипликативной.
Группа G называется конечной, если количество её элементов может быть выражено целым неотрицательным числом. В противном случае группа бесконечна.
Число элементов в конечной группе называют порядком группы.
Теорема.
Определение I и II группы эквивалентны между собой.
Для доказательства теоремы нужно показать, что из определения I следует определение II. Для определенности будем считать, что в G операция *=∙(умножение).
1. Покажем, что из I следует II.
Доказательство.
Пусть G группа по определению I, это значит операция *=∙, удовлетворяет трем аксиомам. Нужно показать, что G группа по определению II, т.к. 1 аксиомы одинаковы, то достаточно проверить выполнимость второй аксиомы определения II, то есть "a,bÎG, a*x=b, y*a=b.
Проведем доказательство для уравнения a*x=b. Для второго уравнения - аналогично.
Т.к. aÎG, то по аксиоме 3, $ 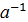 ÎG, т.к.
ÎG, т.к. 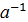 ,bÎG, то
,bÎG, то 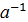 ⋅bÎG, т.к. G замкнуто относительно операции умножения, иначе, операция умножения является бинарной алгебраической операцией на множестве G.
⋅bÎG, т.к. G замкнуто относительно операции умножения, иначе, операция умножения является бинарной алгебраической операцией на множестве G.
Покажем, что элемент 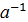 ⋅b является решением уравнения a⋅x=b, a⋅(
⋅b является решением уравнения a⋅x=b, a⋅( 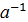 ⋅b)=(a⋅
⋅b)=(a⋅ 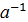 )⋅b=1⋅b=b.
)⋅b=1⋅b=b.
Покажем, что найденное решение единственное:
Предположим, что наряду c x, есть решение 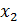 , a⋅
, a⋅ 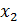 =b.
=b.
То есть, a⋅ 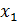 =a⋅
=a⋅ 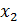 – умножим обе части на
– умножим обе части на 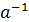 слева.
слева.
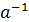 (a⋅
(a⋅ 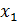 )=
)= 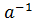 (a⋅
(a⋅ 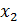 ), (
), ( 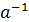 ⋅a)⋅
⋅a)⋅ 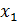 =(
=( 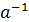 ⋅ a)⋅
⋅ a)⋅ 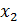 , 1⋅
, 1⋅ 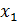 =1⋅
=1⋅ 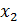 ,
, 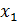 =
= 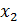 .
.
Вывод: выполнилась 2 аксиома определения II®G группа по определению II.
2. Докажем, что II®I.
Доказательство.
Пусть G группа по определению II, это значит в G выполнимы 2 аксиомы, нужно доказать, что G группа по определению I, а это значит показать выполнимость аксиом 2 и 3 по определению I.
Покажем выполнимость аксиомы 2, "aÎG, a⋅ 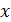 =a.
=a.
По определению II это уравнение имеет единственное решение, обозначим его через 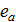 (е с индексом а), и назовем правым единичным элементом для элемента а, а⋅
(е с индексом а), и назовем правым единичным элементом для элемента а, а⋅ 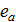 =а.
=а.
Покажем ,что 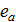 является правым единичным элементом, для любого элемента bÎG.
является правым единичным элементом, для любого элемента bÎG.
Рассмотрим уравнение y⋅a=b, это уравнение имеет единственное решение, 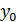 ÎG,
ÎG, 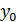 ⋅а=b.
⋅а=b.
Умножим обе части последнего равенства на 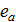 справа, получили: (
справа, получили: ( 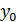 ⋅а)⋅
⋅а)⋅ 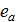 =b⋅
=b⋅ 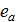 , (
, ( 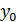 ⋅а)⋅
⋅а)⋅ 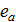 =
= 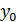 ⋅(а⋅
⋅(а⋅ 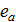 ).
).
Получили b=b⋅ 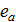 .
.
Получили, что 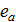 – есть правая единица для любого элемента из G.
– есть правая единица для любого элемента из G.
Обозначим её е′.
Аналогично, если рассматривать уравнение y⋅a=a, можно доказать существование в G левого единичного элемента. Обозначим его е′′.
Докажем: е′′= е′=е=1. 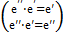 ®
®  =е=1.
=е=1.
Проверим выполнение аксиомы 3 по определению I.
Рассмотрим уравнение вида: а⋅ 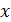 =1 и а⋅y=1.
=1 и а⋅y=1.
Эти уравнения имеют единственное решение обозначим их а′ и а′′ - соответственно.
Получили верные равенства, а⋅а′=1 и а′′⋅а=1.
Рассмотрим 3 элемента принадлежащие G, по аксиоме 1 справедливо равенство, а′′⋅(а⋅а′)=(а′′⋅а)⋅а′. 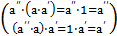 ® а′′=а′=
® а′′=а′= 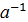 .
.
Выполнилась 3 аксиома определения I ® G – группа по определению I, и определения I и II эквивалентны.
ч.т.д.
Если нужно доказать, что некоторое множество G образует группу относительно операции (*) нужно проверить выполнимость следующих требований:
1. Будет ли операция (*) бинарной алгебраической на множестве G. Будет ли G замкнуто по операции (*).
2. Будет ли операция (*) ассоциативной на множестве G, здесь же проверяют будет ли операция (*) коммутативна.
3. Доказывают наличие нейтрального элемента относительно операции (*).
4. Доказывают, что для " элемента из G, $ в G ему симметричный.
Заметим, что вместо проверки выполнимости требований 3 и 4 можно проверять выполнимость в G обратной операции (*).
Можно дать следующее определение группы:
Определение.
Непустое множество G называется группой, если в нем выполнима одна бинарная алгебраическая операция ассоциативность, причем для этой операции в G выполнима ей обратная.
Простейшие свойства групп:
1. Существует единственный элемент еÎG, такой что "аÎG, а⋅е=е⋅а=а.
Доказательство следует из доказательства эквивалентности двух определений группы. Действительно, предположим, что в G существует два нейтральных элемента, 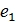 ⋅
⋅ 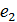 ÎG.
ÎG.
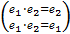 ®
® 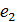 =
= 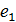 =е.
=е.
2. "аÎG, $! 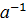 ÎG, а⋅
ÎG, а⋅ 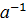 =
= 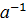 ⋅а=1.
⋅а=1.
3. В G можно однозначно говорить о произведении любых трех элементов из G более того можно однозначно говорить о произведении любого конечно числа элементов из G.
4. " 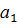 ,
, 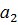 ,…,
,…, 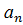 ÎG,
ÎG, 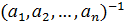 =
= 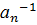 ⋅
⋅ 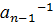 ⋅…⋅
⋅…⋅ 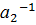 ⋅
⋅ 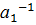 ,
,
( 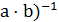 =
= 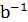 ⋅
⋅ 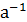
Действительно, ( 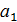 ⋅
⋅ 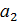 ⋅…⋅
⋅…⋅ 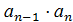 )⋅(
)⋅( 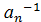 ⋅
⋅ 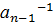 ⋅…⋅
⋅…⋅ 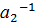 ⋅
⋅ 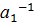 )=1.
)=1.
С другой стороны, 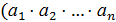 )⋅
)⋅ 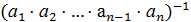 =1, таким образом получим, что
=1, таким образом получим, что 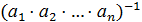 =
= 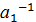 ⋅
⋅ 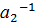 ⋅…⋅
⋅…⋅ 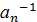 .
.
Примеры групп:
1. (N,+) – не группа, так как нет нуля;
2. (Z,+), Z={…,-3,-2,-1,0,1,2,3,…} – аддитивная абелева бесконечная группа целых чисел;
3. (Q,+), (R,+), (C,+) – бесконечные аддитивные абелевы группы;
4. (Z,⋅) – не группа, так как не для " есть обратный элемент;
5. (Q,⋅) – не группа, для нуля нет обратного;
6. (Q\{0},⋅) – мультипликативная бесконечная абелева группа;
7. (R\{0},⋅), (C\{0},⋅) – мультипликативные абелевы группы;
8. 

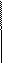
 G={1;-1}, (G,⋅), если множество конечно составляем таблицу Кэли.
G={1;-1}, (G,⋅), если множество конечно составляем таблицу Кэли. 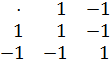
1. Операция ⋅ (точка) бинарная алгебраическая операция на G.
2. GÌZ, коммутативно и ассоциативно в G.
3. 1ÎG.
4. Для 1 обратный элемент 1, для -1 обратный -1.
G – конечная мультипликативная абелева группа второго порядка.
9. G={1, i, -1, -i}, (G,⋅),
1. Операция (⋅) (точка) бинарная алгебраическая операция.
2. Так как GÌC, а в C умножение коммутативно и ассоциативно, то умножение коммутативно и ассоциативно в G, как на подмножестве C. Если таблица Кэли симметрично относительно диагонали, то операция коммутативна.
3. 1ÎG.
4. 1 обратный элемент 1, для -1 обратный -1, для i обратный элемент i, для –i обратный –i.
Конечная мультипликативная группа четвертого порядка.
 Пример, конечная мультипликативная группа корней n-ой степени из 1 порядка n. y
Пример, конечная мультипликативная группа корней n-ой степени из 1 порядка n. y
 1=1+0⋅1, 1=1(cos0+isin0) 0 x
1=1+0⋅1, 1=1(cos0+isin0) 0 x
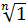 =
=  =cos
=cos 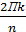 +isin
+isin 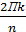 , k=
, k= 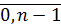 ,
,
G={ 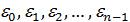 },
},
n=2,
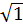 =( cos
=( cos 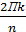 +isin
+isin 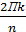 )=cosПk+isinПk, kÎZ.
)=cosПk+isinПk, kÎZ.
k=0,
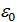 =cos0+isin0=1,
=cos0+isin0=1,
k=1,
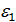 = cosП+isinП=-1,
= cosП+isinП=-1,
G={1,-1}.
n=3,
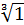 = cos
= cos 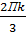 +isin
+isin 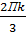 , k=0,1,2;
, k=0,1,2;
k=0,
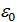 =cos0+isin0=1,
=cos0+isin0=1,
k=1,
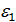 = cos
= cos 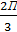 +isin
+isin 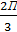 =-
=- 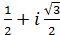 ,
,
k=2,
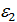 = cos
= cos  +isin
+isin  =-
=- 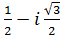 ,
,
G={1, - 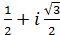 , -
, - 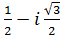 }.
}.
n=4,
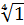 = cos
= cos 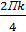 +isin
+isin 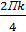 = cos
= cos 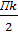 +isin
+isin 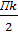 , k=0, 1, 2, 3;
, k=0, 1, 2, 3;
k=0,
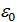 =cos0+isin0=1,
=cos0+isin0=1,
k=1,
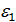 = cos
= cos  +isin
+isin  =i,
=i,
k=2,
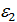 =cosП+isinП=-1,
=cosП+isinП=-1,
k=3,
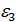 = cos
= cos 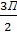 +isin
+isin 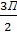 =-i,
=-i,
G={1;i;-1;-i}.
Пусть дано множество G корней n-ой степени из 1.
G={ 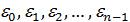 }.
}.
Покажем, что G образует мультипликативную абелеву группу n-го порядка.
(G,⋅)
1. " 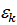 ,
, 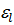 ÎG,
ÎG, 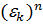 =1,
=1, 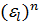 =1; докажем, что
=1; докажем, что 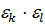 ÎG,
ÎG, 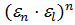 =
= 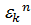 ⋅
⋅ 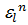 =1⋅1=1 ⇨
=1⋅1=1 ⇨ 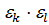 ÎG.
ÎG.
2. GÌC, а в C – умножение ассоциативно и коммутативно ⇨ умножение ассоциативно и коммутативно в G как на подмножестве C.
3. 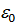 =1, "n ⇨ 1ÎG.
=1, "n ⇨ 1ÎG.
4. " 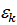 ÎG,
ÎG, 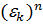 =1 обратный элемент
=1 обратный элемент 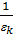 , так как
, так как 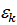 ⋅
⋅ 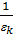 =1,
=1, 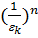 =
= 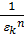 =
=  =1 ⇨
=1 ⇨ 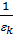 ÎG.
ÎG.
Таким образом, множество корней n-ой степени из 1, есть конечная мультипликативная абелева группа n-го порядка.
Определение. Корень 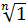 называют первообразным корнем, если он только в n-ой степени даёт единицу, и ни в какой меньшей степени, чем в n единицы не даёт.
называют первообразным корнем, если он только в n-ой степени даёт единицу, и ни в какой меньшей степени, чем в n единицы не даёт.
Пример, 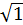 ={1;-1}=G, 1ÎG,
={1;-1}=G, 1ÎG, 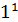 =1 – не первообразный корень, -1ÎG, -1 – первообразный корень.
=1 – не первообразный корень, -1ÎG, -1 – первообразный корень.
Пример 2, G= 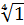 ={1, i, -1, -i},
={1, i, -1, -i},
1ÎG, 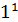 =1 – не первообразный корень,
=1 – не первообразный корень,
i ÎG, 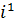 =I,
=I, 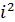 =-1,
=-1, 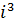 =-i,
=-i, 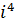 =1, i – первообразный корень,
=1, i – первообразный корень,
-1ÎG, 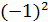 =1 – не первообразный корень,
=1 – не первообразный корень,
-iÎG, 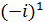 =-i,
=-i, 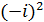 =-1,
=-1, 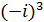 =i,
=i, 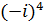 =1, i – первообразный корень.
=1, i – первообразный корень.
Справедливо утверждение: Корень 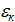 будет первообразным корнем n-ой степени из единицыÛкогда k и n взаимно просты.
будет первообразным корнем n-ой степени из единицыÛкогда k и n взаимно просты.
Пример 3, пусть G= 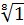 ={
={  },
},
D(1,8)=1, 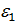 – первообразный корень,
– первообразный корень,
D(2,8)=2, 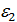 - не первообразный корень,
- не первообразный корень,
D(3,8)=1, 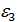 - первообразный корень,
- первообразный корень,
D(4,8)=4, 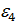 - не первообразный корень,
- не первообразный корень,
D(5,8)=1, 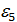 - первообразный корень,
- первообразный корень,
D(6,8)=2, 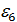 - не первообразный корень,
- не первообразный корень,
D(7,8)=1, 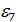 -первообразный корень.
-первообразный корень.
Пример 4, G= 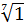 ,
, 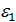 ,
, 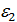 ,
, 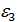 ,
, 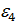 ,
, 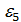 ,
, 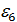 ,
, 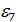 – все первообразные корни.
– все первообразные корни.
Справедливо следующее свойство первообразных корней:
Если 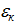 - первообразный корень
- первообразный корень 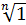 , то числа
, то числа 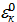 ,
, 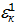 ,
, 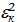 ,…,
,…, 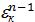 совпадают с корнями n-ой степени из единицы.
совпадают с корнями n-ой степени из единицы.
ГРУППА ПОДСТАНОВОК n -ОЙ СТЕПЕНИ.
Пусть дано множество, состоящее из n элементов. В частности, множество первых n натуральных чисел. Всякое расположение n элементов в некотором определенном порядке называют перестановкой из n-элементов.
$n! перестановок из n элементов.
Запишем 2 перестановки одну под другой получим подстановку n-ой степени.
Определение.
Всякое взаимно однозначное отображение n-элементов на себя называют подстановкой n-ой степени или всякое взаимно-однозначное отображение первых n натуральных чисел на себя называется подстановкой n-ой степени.
Пример 1, ( 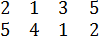
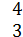 )= (
)= ( 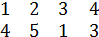
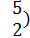 .
.
$n! подстановок n-ой степени.
Любую подстановку n-ой степени можно записать так, что первая подстановка идет в обычном порядке, это значит количество разных подстановок зависит от количества различных вторых перестановок.
Различных постановок n-ой степени будет n!
Обозначим множество всех подстановок n-ой степени через 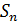 .
.
Покажем, что множество 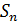 образует конечную мультипликативную группу порядка n!
образует конечную мультипликативную группу порядка n!
Для этого на множестве 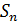 введем операцию умножение подстановок.
введем операцию умножение подстановок.
Под произведением двух подстановок n-ой степени понимают результат двух последовательно взаимно-однозначных отображений n-элементов на себя.
Из определения следует, что результатом произведения двух подстановок n-ой степени будет снова подстановка n-ой степени.
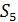 , "А, ВÎ
, "А, ВÎ 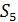 ,
,
А=( 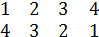
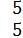 ), В=(
), В=( 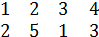
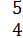 ),
),
А⋅В=( 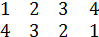
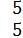 )⋅(
)⋅( 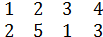
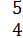 )=(
)=( 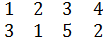
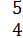 ),
),
В⋅А=( 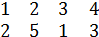
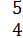 )⋅(
)⋅( 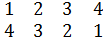
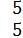 )=(
)=( 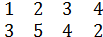
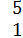 ).
).
Множество  замкнуто относительно операции умножения.
замкнуто относительно операции умножения.
Покажем, что операция умножения подстановок ассоциативна:
"А, В, СÎ 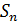 ,
,
(А⋅В)⋅С=А⋅(В⋅С),
А: α®β,
В: β®γ,
С: γ®δ.
А⋅В: α® γ, (А⋅В) ⋅С: γ®δ, (А⋅В) ⋅С= α® δ, В⋅С: β® δ, А⋅(В⋅С): α® δ.
Роль единичного элемента выполняет, так называемая единичная или тождественная подстановка, которая каждый элемент оставляет на месте.
Е=( 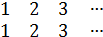
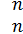 ), Е=(
), Е=( 
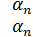 ).
).
"АÎ 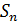 , А⋅Е= Е⋅А=А
, А⋅Е= Е⋅А=А
А=( 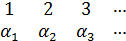
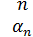 ), $
), $ 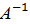 =(
=( 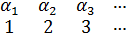
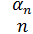 ).
).
Таким образом, множество всех подстановок степени n образует в общем случае не абелеву мультипликативную конечную группу порядка n!, её называют симметрической группой подстановок n-ой степени.
ПОДГРУППЫ. КРИТЕРИИ ПОДГРУПП.
Пусть дана для определенности мультипликативная группа G:
(G,⋅), АÌG, множество А¹Æ, называют подгруппой группы G, если оно само образует группу относительно операции определенной в G.
Критерии подгрупп:
Для того чтобы не пустое подмножество А группы G, было подгруппой группы G, необходимо и достаточно, чтобы выполнялись 2 требования:
1.)"а,bÎA, a⋅bÎA;
2.)"aÎA, $ 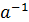 ÎA;
ÎA;
Доказательство:
I. Необходимость;
Дано: (G,⋅) – группа, А – подгруппа G.
Доказать: выполнимость 1 и 2.
Так как А подгруппа G, то А образует группу относительно заданной операции ⇨ А замкнута относительно операции и для " элемента из А есть ему обратный.
II. Достаточность;
Дано: (G,⋅) – группа, А¹0, АÍ G, выполняются 1 и 2 условия.
Доказать: А – подгруппа группы G.
Чтобы доказать, что А – подгруппа группы G нужно доказать, что А образует группу относительно заданной операции, таким образом проверить все требования определяющие группу:
Из выполнимости требования 1 следует, что операция умножения является бинарной алгебраической операцией на множестве А. Операция умножения ассоциативна в А, как на подмножестве группы G. Из выполнимости требования 2 для "аÎА, $ 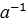 ÎА. Из выполнимости требования 1 а⋅
ÎА. Из выполнимости требования 1 а⋅ 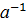 =
= 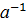 ⋅а=1, 1ÎА. Достаточность доказана, так как АÍ G, то А является подгруппой группы G. У всех подгрупп один и тот же нейтральный элемент, это нейтральный элемент группы G и одна и та же бинарная алгебраическая операция, которая задана в G.
⋅а=1, 1ÎА. Достаточность доказана, так как АÍ G, то А является подгруппой группы G. У всех подгрупп один и тот же нейтральный элемент, это нейтральный элемент группы G и одна и та же бинарная алгебраическая операция, которая задана в G.
Примеры подгрупп:
1. Любая группа для себя является подгруппой.
2. Подмножество состоящее из одного нейтрального элемента данной группы является её подгруппой.
Примеры 1 и 2 – это примеры не собственных подгрупп группы G, любая другая подгруппа группы G, если она есть называется собственной подгруппой группы G.
3. (Z,+) подгруппа (Q,+) подгруппа (R,+) подгруппа (C,+).
4. (G\ {0},⋅) подгруппа (R\ {0},⋅) подгруппа (C\ {0},⋅).
5. А={k⋅n|/kÎN, n ÎZ} – множество целых чисел кратных к.
(А,+) – аддитивная абелева группа, АÍZ, (А,+) подгруппа для (Z,+).
Дата добавления: 2018-11-24; просмотров: 1262; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
