Гомоморфизм групп. Свойства гомоморфизма.
Определение.
Группа (G,*) называется гомоморфной группе (G’,∙), если между ними можно установить такое однозначное отображение j группы g на группу G’, при котором "a,bÎG и соответствующих им j(a), j(b)ÎG выполняется условие:
Заметим, что операция в G и G’ не обязательно одинаковые. Если дано (G,*) и (G’,°), тогда j(a*b)= j(a)°j(b), (образ произведения равен произведению образов). j
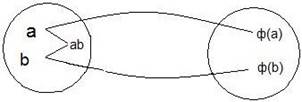
G G’
Справедливы следующие свойства гомоморфных групп:
Пусть G гомоморфная к G’ .
1) 1ÎG соответствует 1ÎG’ (нейтральный элемент группы G соответствует нейтральному элементу группы G’).
Доказательство:
"аÎG, а®j(а)=а’ÎG, 1ÎG, и пусть 1®j(1)=b’ÎG,
а’=j(а)= j(а⋅1)= j(а)⋅ j(1)= а’⋅b’,
а’=j(а)= j(1⋅а)= j(1)⋅ j(а)= b’⋅а’,
а’⋅b’= b’⋅а’=а’⇨ b’=1, а так как b’=j(1), j(1)=1’.
Ч.т.д.
2) Обратные элементы к соответствующим, соответствуют друг другу.
j( 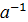 )=
)= 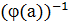 .
.
Доказательство:
"аÎG, а®j(а)=а’ÎG’, так как G – группа, то $ 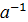 ÎG,
ÎG, 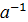 ®j(
®j( 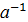 )=с’ÎG.
)=с’ÎG.
Тогда, 1’=j(1’)=j(a⋅ 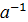 )=j(a)⋅j(
)=j(a)⋅j( 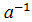 )=a’⋅c’,
)=a’⋅c’,
1’=j(1’)=j( 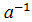 ⋅a)=j(
⋅a)=j( 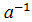 )⋅j(a)=c’⋅a’,
)⋅j(a)=c’⋅a’,
a’⋅c’= c’⋅a’=1’⇨ c’= 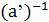 , c’=j(
, c’=j( 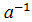 ), j(
), j( 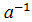 )=
)= 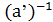 =(j
=(j 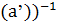 .
.
Ч.т.д.
|
|
|
3) Если группа G абелева, то и гомоморфная ей группа G’ так же Абелева.
Доказательство: так как G-абелева, то "a,bÎG: a⋅b= b⋅a,
j(a⋅b)=j(a)⋅j(b),
j(b⋅a)=j(b)⋅ j(a),
j(a)⋅j(b)= j(b)⋅ j(a) - коммутативность⇨G – Абелева группа.
Ч.т.д.
Примеры,
1) G=(Z,+) аддитивная группа целых чисел, G=({1,-1},⋅).
Доказать: G гомоморфная G’.
Доказательство: Установим отображение j между группами G и G’, "аÎG, и а®1, если а - четное, и а®-1, если а – нечетное.
j отображение на.
Возможны случаи:
1. а – четное, b – четное, а+b – четное, j(а)=1, j(b)=1, j(а+b)=1=1⋅1=j(а)⋅j(b).
2. а – четное, b – нечетное, а+b – нечетное, j(а)=1, j(b)=-1, j(а+b)=1⋅(-1)=j(b)⋅j(a).
3 и 4 случаи аналогичны.
ИЗОМОРФИЗМ ГРУПП.
Пусть даны две определенные мультипликативные группы: (G,⋅) и (G’,⋅).
Определение. Группа G называется изоморфной группе G’, если между ними можно установить такое взаимно однозначное отображение j группы G на G’: "а,bÎG, и j(a),j(b)ÎG’, выполняется:
j(a⋅b)= j(a)⋅j(b).
В общем случае (G,*) и(G’,°) j(a*b)= j(a)°j(b).
|
|
|
Понятие изоморфизма групп является частным случаем гомоморфизма групп. Или изоморфизм групп – это взаимно однозначный гомоморфизм групп. Так как изоморфные группы будут гомоморфными, то все свойства гомоморфных групп справедливы для изоморфных групп. Для изоморфных групп справедливы так же следующие свойства:
4) G изоморфна G’ – рефлективность, зададим отображение j группы G на себя, "аÎG, а®j(а)=а, j(а)ÎG.
Если а¹b, то j(а)¹ j(b), "а,bÎR.
Значит, j-взаимно-однозначное соотношение.
j(а⋅b)=а⋅b=j(а)⋅j(b).
Ч.т.д.
5) Если G изоморфна G’, то G’ изоморфна G – симметричность.
Доказательство: Пусть G изоморфна G’, значит между ними установлено взаимно-однозначное соотношение группы G на G’.
("аÎG, а®j(а)=а’ÎG’), "а,bÎG, а¹b⇨j(а)¹ j(b), а¹b и j(а⋅b)= а¹b⇨j(а)⋅j(b).
Докажем, что G’ изоморфно G. Для этого между G’ и G нужно установить отображение группы G’ на G, показать, что оно взаимно однозначное, и что оно сохраняет операции между соответствующими элементами. Зададим отображение y группы G’ на G следующим образом:
"а’ÎG’, a’®y(a’)=a, где j(a)=a’.
|
|
|
Тогда j(a’)=y( j(a))=a.
y - отображение на по способу его задания.
"a’, b’ÎG’, a’¹b’⇨j(a)¹j(b)⇨a¹b⇨y(a’)¹y(b’), значит y - взаимно-однозначно.
Найдем ⇨y(a’⋅b’)=y(j(a)⋅j(b))=y(j(a⋅b))=a⋅b=y(a’)⋅y(b’).
Получили, что y(a’⋅b’)=y(a’)⋅y(b’)⇨ G’ изоморфна G.
6) Если G изоморфна G’ и G’ изоморфна G, то G изоморфна G’’-свойство транзитивности.
Бинарное отношение “быть изоморфным” заданное на множестве групп, удовлетворяет свойствам рефлексивности, симметричности и транзитивности ⇨ оно является отношением эквивалентности и разбивает множество всех групп на непересекающиеся классы изоморфных между собой групп. С алгебраической точки зрения изоморфные группы считаются неразличимыми. Все свойства доказанные для одной из групп будут справедливы и для всех групп ей изоморфных, при условии, что при доказательствах не затрагивались индивидуальные свойства элементов данной группы, а использовались только свойства заданной операции.
Если доказано, что группа G изоморфна какому либо множеству относительно заданной на нем операции, то это множество так же образует группу относительно заданной операции.
ПОРЯДОК ЭЛЕМЕНТА ГРУППЫ. ЦИКЛИЧЕСКИЕ ПОДГРУППЫ.
|
|
|
Пусть дана мультипликативная группа G. Возьмем "аÎG, nÎN,
а⋅а⋅а⋅а⋅…⋅а= 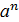 .
.
Произведение n элементов равных а называют n-ой степенью элемента а.
n=0, 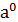 =1, n<0, nÎZ.
=1, n<0, nÎZ.
Целой отрицательной степенью элемента а называют элемент обратный к целой положительной степени элемента а, или произведение n-элементов равных 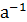 .
.
(а⋅а⋅а⋅…⋅а)⋅( 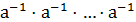 )=1,
)=1,
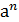 ⋅
⋅ 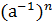 =1,
=1,
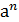 ⋅
⋅ 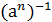 =1,
=1,
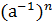 =
= 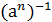 =
= 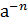 .
.
Свойства степеней:
1. 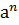 ⋅
⋅ 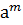 =
= 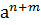 ;
;
2. 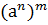 =
= 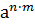 , где n,mÎZ;
, где n,mÎZ;
Возьмем "аÎG и рассмотрим множество состоящее из целых степеней элемента а, обозначив его (а):
(а)={ 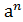 /nÎZ}, (а)ÍG,
/nÎZ}, (а)ÍG,
Покажем, что (а) образует подгруппу группы G. Для доказательства воспользуемся критерием подгруппы.
1. Возьмем " 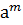 ,
, 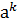 Î(а), m,kÎZ,
Î(а), m,kÎZ, 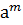 ⋅
⋅ 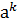 =
= 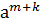 Î(a), так как (m+k)ÎZ;
Î(a), так как (m+k)ÎZ;
2. " 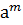 Î(а), mÎZ, так как -mÎZ, то
Î(а), mÎZ, так как -mÎZ, то 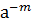 Î(а),
Î(а), 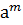 ⋅
⋅ 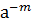 =
= 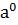 =1,
=1, 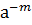 =
= 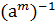 ⇨(а) подгруппа группы G.
⇨(а) подгруппа группы G.
Такие подгруппы которые порождены элементом аÎG называют циклическими подгруппами.
Определение.
Подгруппа (а) состоящая из целых степеней элемента а группы G называют циклической подгруппой группы G.
Определение.
Элемент а называют порождающим или образующим элементом для данной циклической подгруппы.
Замечание. Если операция в группе G сложение, то а+а+а+…+а=n⋅а, nÎN. Если n=0, 0⋅а=0, (-а)+(-а)+(-а)+…+(-а)=-n⋅а.
Заметим, что циклическую подгруппу группы G можно образовать с помощью " элемента из данной группы.
Пусть дана для определенности (G,⋅).
"аÎG и образуем циклическую подгруппу, порожденную элементом а.
(а)={ 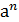 | nÎZ}.
| nÎZ}.
Возможны случаи:
1. Все целые степени элемента а различны между собой, тогда порожденная элементом а циклическая подгруппа будет бесконечного порядка.
2. Может оказаться, что среди целых степеней элемента а будут равные.
G=({-1,1},⋅), -1ÎG – образуют циклическую подгруппу.
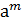 =
= 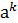 , где m¹k.
, где m¹k.
Пусть для определенности m>k. Умножим обе части равенства 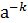 ÎG,
ÎG, 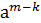 =
= 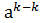 =
= 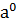 =1, m-k>0, приходим к понятию порядка элемента а группы G.
=1, m-k>0, приходим к понятию порядка элемента а группы G.
Определение. Порядком элемента (а) группы G называется наименьшее натуральное число n, такое что 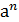 =1.
=1.
Пусть порядок элемента а группы G равен n, тогда справедлива теорема:
ТЕОРЕМА.
Если элемента а группы G имеет порядок n, то все элементы группы вида 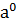 ,
, 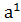 ,
, 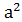 ,…,
,…, 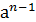 различны между собой и любая другая степень элемента а совпадает с одним из записанных элементов.
различны между собой и любая другая степень элемента а совпадает с одним из записанных элементов.
Доказательство:
Пусть порядок элемента а равен n, n – наименьшее натуральное число удовлетворяющее этому равенству или условию доказательства, проведем методом от противного, предположим, что среди указанных элементом есть равные: 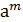 =
= 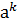 , m¹k.
, m¹k.
Пусть для определенности m>k, умножим обе части последнего равенства на 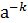 ,
, 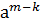 =
= 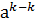 =
= 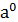 =1.
=1.
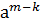 =1, где 0<m-k<n.
=1, где 0<m-k<n.
Получили противоречие с определением порядка элементов группы, следовательно все данные элементы различны между собой, а любая другая степень совпадает с одним из этих элементов.
Возьмем " 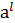 , lÎG, lÎ(a),
, lÎG, lÎ(a), 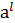 Î(a) к числам l и n применим теорему о делении с остатком.
Î(a) к числам l и n применим теорему о делении с остатком.
l=n⋅q+r, 0 £ r £ n-1, тогда 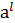 =
= 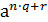 =
= 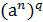 ⋅
⋅ 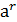 =
= 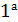 ⋅
⋅ 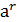 =
= 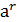 ,
, 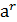 - среди указанных элементов.
- среди указанных элементов.
Циклическая подгруппа порожденная элементом аÎG конечного порядка n сама будет конечной так же n-го порядка, она состоит из элементов 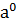 ,
, 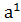 ,
, 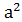 ,…,
,…, 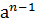 ,
, 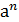 =1.
=1.
Порядок элемента всегда совпадает с порядком порожденной им циклической группы.
ч.т.д
Пример, Пусть дана группа мультипликативная 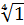 , найти порядки элементов этой группы и порожденные ими циклические подгруппы.
, найти порядки элементов этой группы и порожденные ими циклические подгруппы.
Будет ли сама группа G циклической?
G=({1, i, -1, -i},⋅)
1ÎG, iÎG, 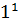 =1, n=1,
=1, n=1,
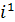 =i,
=i, 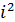 =-1,
=-1, 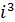 =-i,
=-i, 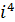 =1,
=1,
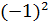 =1,
=1, 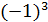 =-1,
=-1,
n=2, -iÎG, 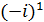 =-i,
=-i, 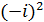 =1,
=1, 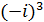 =i,
=i, 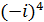 =-1,
=-1,
n=4, (-i)={-i, -1, i, 1}=G.
Таким образом группа G – циклическая её порожденные элементы i и –i.
ЦИКЛИЧЕСКИЕ ПОДГРУППЫ. ВИДЫ ЦИКЛИЧЕСКИХ ПОДГРУПП.
Пусть дана (G,⋅) образуем циклические подгруппы порожденные элементами группы G. Так как любая подгруппа образует группу относительно заданной операции, то приходим к понятию циклической группы.
Определение 1.
Группа называется циклической, если она состоит из целых степеней одного из своих элементов.
Элемент целыми степенями которого образована данная циклическая группа называется порождающим или образующим элементом.
Определение 2.
Группа G называется циклической, если она совпадает с одной из своих циклических подгрупп.
Примером бесконечной циклической группы является аддитивная группа целых чисел: G=(Z,+)
Z={1⋅n|nÎZ}, G=(1)={…,1⋅(-3), 1⋅(-2), 1⋅1, 1⋅0,…}
Примером конечной циклической группы n-ого порядка является мультипликативная группа корней n-ой степени из 1.
Любой из первообразных корней является порождающим элементом этой группы.
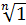
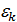 называют первообразным корнем, если он только в n-ой степени дает 1, и ни в какой меньшей степени 1 не дает.
называют первообразным корнем, если он только в n-ой степени дает 1, и ни в какой меньшей степени 1 не дает.
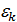 будет первообразным корнем
будет первообразным корнем 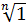 Û когда D(n,k)=1.
Û когда D(n,k)=1.
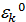 ,
, 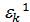 ,
, 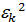 ,…,
,…, 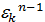 различны, и дают все корни
различны, и дают все корни 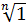 .
.
ВИДЫ ЦИКЛИЧЕСКИХ ГРУПП.
Справедливы следующие теоремы о циклических подгруппах.
Теорема 1.
Все бесконечные циклические группы изоморфны между собой и изоморфны аддитивной группе целых чисел.
Доказательство:
Пусть дана G=(Z,+), G=(1)={1⋅n|nÎZ},
Выберем произвольным образом любую для определенности мультипликативную циклическую группу G¢ с порождающим элементом а.
G¢=(а)={ 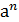 |nÎZ, аÎG},
|nÎZ, аÎG},
Покажем, что G изоморфно G¢, для этого между G и G¢ нужно установить взаимно однозначное отображение j: G на G¢, и показать, что j-изоморфно.
j: "nÎG, n® 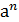 , n=0, n=0, ±1, ±2,…,
, n=0, n=0, ±1, ±2,…, 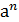 ÎG,
ÎG,
j - отображение “на” по способу задания.
Отображение j взаимно однозначно.
Если 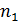 ≠
≠ 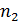 ®
® 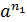 ≠
≠ 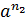 .
.
" 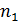 ,
, 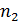 ÎG, j(
ÎG, j( 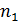 )=
)= 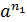 , j(
, j( 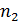 )=
)= 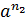 ,
, 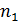 +
+ 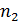 =(
=( 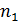 +
+ 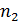 ), j(
), j( 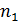 +
+ 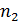 )=j((
)=j(( 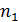 +
+ 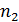 ))=
))= 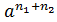 =
= 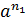 ∙
∙ 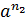 =j(
=j( 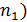 ∙ j(
∙ j( 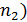 ®j - изоморфизм.
®j - изоморфизм.
G изоморфно G¢.
Ч.т.д.
Так как бинарное отношение «быть изоморфным» заданное на множестве групп, удовлетворяет свойству транзитивности, и циклическую группу G¢ выбирали произвольно, то делаем вывод, что все бесконечные циклические группы изоморфны между собой и изоморфны аддитивной группе целых чисел.
Теорема 2.
Все конечные группы n-го порядка изоморфны между собой и изоморфны мультипликативной группе корней 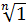 .
.
Доказательство:
Пусть G – мультипликативная группа 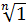 , она циклическая и пусть порождающим элементом является корень e.
, она циклическая и пусть порождающим элементом является корень e.
G=(e)={ 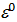 ,
, 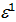 ,
, 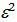 ,…,
,…, 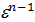 }
}
Выберем произвольным образом конечную, циклическую для определенности мультипликативную группу n-го порядка с образующим элементом а.
G¢(а)={ 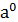 ,
, 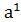 ,
, 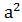 ,…,
,…, 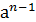 }
}
Доказать, что G изоморфно G¢.
Установим между G и G¢ отображение j следующим образом, возьмем " 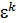 ÎG, к=
ÎG, к= 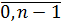 ,
,
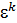 ®
® 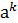 ,
, 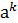 ÎG¢.
ÎG¢.
j есть отображение (на) по способу его задания, т.е. j - взаимно однозначно.
Если 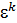 ≠
≠ 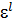 ®k≠l®
®k≠l® 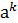 ≠
≠ 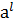 , "
, " 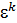 ,
, 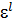 ÎG.
ÎG.
j( 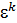 )=
)= 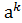 , j(
, j( 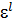 )=
)= 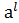 ,
, 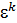 ∙
∙ 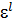 =
= 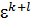 , j(
, j( 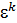 ∙
∙ 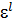 )=j(
)=j( 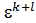 )=
)= 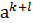 =
= 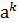 ∙
∙ 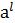 =j(
=j( 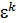 )∙j(
)∙j( 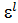 )® G изоморфно G¢.
)® G изоморфно G¢.
Ч.т.д.
В силу того, что G¢ выбирали произвольно и того что бинарное отношение «быть изоморфным» транзитивно, делаем вывод, что все конечные циклические группы n-го порядка изоморфны между собой.
Теорема (о подгруппах циклической группы).
" подгруппа циклической группы сама является циклической.
Доказательство:
Пусть дана определенная мультипликативная циклическая группа G с образующим элементом а.
G=(а), G=(а)={ 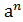 |nÎZ, аÎG }.
|nÎZ, аÎG }.
А - " подгруппа группы G.
А=(1), то А – циклическая.
Если А=G, то А – циклическая.
Пусть А собственная подгруппа группы G.
"bÎА, пусть b= 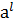 , lÎZ.
, lÎZ.
Обозначим через 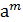 – элемент принадлежащий А, но такой у которого m – есть наименьшее натуральное число,
– элемент принадлежащий А, но такой у которого m – есть наименьшее натуральное число, 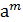 ÎА.
ÎА.
Покажем, что 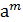 будет образующим элементом подгруппы А, а значит подгруппа А будет циклической.
будет образующим элементом подгруппы А, а значит подгруппа А будет циклической.
Применим к числам l и m, теорему о делении с остатком.
l=m∙q+r, 0 £ r £ n-1, тогда b= 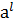 =
= 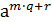 =
= 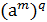 ⋅
⋅ 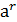 .
.
Относительно r возможно 2 случая:
1. r≠0, так как 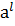 ÎА,
ÎА, 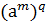 ÎА, тогда
ÎА, тогда 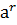 ÎА.
ÎА.
Пришли к противоречию, так как получили, что 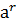 ÎА, где r<m, то есть к противоречию с выбором показателя m.
ÎА, где r<m, то есть к противоречию с выбором показателя m.
2. r=0, b= 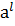 =
= 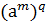 , где qÎZ, так как b выбирали произвольно, то делаем вывод, что " элемент из подгруппы А является целой степенью элемента
, где qÎZ, так как b выбирали произвольно, то делаем вывод, что " элемент из подгруппы А является целой степенью элемента 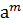 ÎА, следовательно
ÎА, следовательно 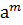 есть образующий элемент, для подгруппы А, а значит подгруппа А циклическая.
есть образующий элемент, для подгруппы А, а значит подгруппа А циклическая.
Так как подгруппа А выбиралась произвольно, то " подгруппа циклической группы сама будет циклической.
Конечные группы, Теорема Кэли.
Группа G называется конечной, если число её элементов конечно, число элементов конечной группы называется порядком группы. Чтобы выяснить будет ли конечное множество образовывать группу относительно заданной операции, нужно проверить выполнимость следующих требований:
1. Будет ли заданная операция БАО на данном множестве, иначе, будет ли множество замкнутым относительно заданной операции, обязательно нужно составить таблицу Келли.
2. С помощью таблицы Келли проверяют будет ли заданная операция ассоциативной и коммутативной. Если таблица симметрична относительно главной диагонали, то операция не коммутативна.
3. Наличие нейтрального элемента.
4. Для любого элемента должен существовать ему симметричный.
Относительно конечных групп n – ого порядка, справедлива теорема Келли, которая дает возможность свести изучения всех конечных групп n – ого порядка, к изучению подгрупп n – ого порядка симметрической группы 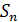 , подстановок n – ой степени.
, подстановок n – ой степени.
Теорема.
Любая конечная группа n - ого порядка изоморфна некоторой подгруппе n - ого порядка симметричной группы подстановок n – ой степени.
Доказательство:
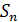 =n!
=n!
Выберем произвольным образом для определенности мультипликативную группу G n – ого порядка.
Пусть группа G состоит из элементов G={ 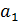 ,
, 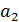 ,…,
,…, 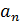 }, "
}, " 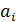 ÎG, i=
ÎG, i= 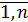 .
.
Составим произведение 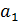 ∙
∙  ,
, 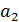 ∙
∙  ,…,
,…, 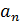 ∙
∙  ÎG.
ÎG.
Так как G замкнуто относительно операции умножения покажем, что полученные элементы различны между собой, предположим противное.
Пусть 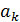 ∙
∙  =
= 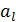 ∙
∙  , так как
, так как  ÎG, а G – группа, то существует
ÎG, а G – группа, то существует 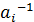 ÎG. Умножим обе части последнего равенства на
ÎG. Умножим обе части последнего равенства на 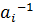 справа.
справа.
( 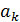 ∙
∙  )∙
)∙ 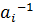 =(
=( 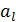 ∙
∙  )∙
)∙ 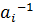 ,
,
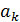 ∙
∙ 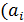 ∙
∙ 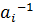 )=
)= 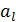 ∙(
∙(  ∙
∙ 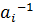 ),
),
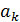 ∙1=
∙1= 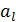 ∙1 ®
∙1 ® 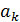 =
= 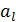 .
.
Пришли к противоречию, так как 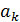 ,
, 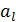 ÎG, а в группе все элементы различны между собой.
ÎG, а в группе все элементы различны между собой.
Мы доказали, что выписанные произведения на  есть различные элементы группы G.
есть различные элементы группы G.
Элементу  поставим в соответствие подстановку следующего вида:
поставим в соответствие подстановку следующего вида:
 ® ®
® ® 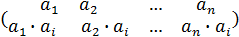 =(
=( 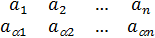 )=(
)=( 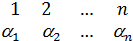 )Î
)Î 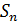
" 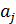 ® ®(
® ®( 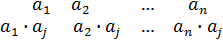 )=(
)=( 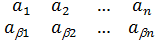 )=(
)=( 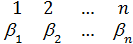 )Î
)Î 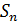
И такие подстановки поставим в соответствие каждому элементу из группы G, получим n подстановок указанного вида.
Покажем, что все эти подстановки различны между собой.
Действительно элемент еÎG в подстановке, которая соответствует 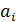 , отобразится на элемент
, отобразится на элемент  : е∙
: е∙  =
= 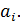
Этот же элемент еÎG в подстановке, которая соответствует 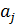 , отобразится на элемент
, отобразится на элемент 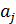 : е∙
: е∙ 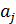 =
= 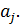
А так как  ≠
≠ 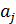 , то и подстановки соответствующие различным элементам будут различны между собой.
, то и подстановки соответствующие различным элементам будут различны между собой.
Обозначим через G¢ множество полученных подстановок.
G¢Ì 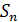 и состоит из различных подстановок.
и состоит из различных подстановок.
Докажем, что G¢ изоморфно G.
Установим между G и G¢ отображение j следующим образом:
"  ÎG,
ÎG,  ®j(
®j(  )=(
)=( 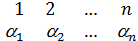 ),
),
" 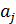 ÎG,
ÎG, 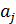 ®j(
®j( 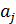 )=(
)=( 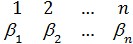 )=(
)=( 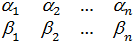 ).
).
Установленное отображение j группы G на множество G¢ является взаимно однозначным.
Покажем, что j - изоморфно.
То есть нужно доказать j(  ∙
∙ 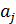 )= j(
)= j(  )∙j(
)∙j( 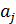 ),
),
j(  ∙
∙ 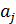 )=(
)=( 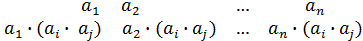 )=(
)=( 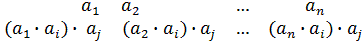 )=
)=
=( 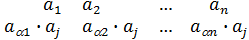 )=(
)=( 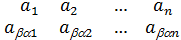 )=
)=
=( 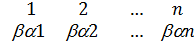 )=(
)=( 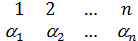 )∙(
)∙( 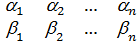 )=
)=
=j 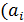 )∙j
)∙j 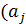 ).
).
Таким образом j - изоморфизм G на G¢ ® G¢ - группа n – го порядка, а так как G¢Ì 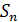 , то G¢ подгруппа группы
, то G¢ подгруппа группы 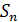 .
.
Ч.т.д.
Дата добавления: 2018-11-24; просмотров: 514; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
