Лабораторная работа № 11. Численное дифференцирование с помощью интерполяционных формул Лагранжа и Ньютона
Задания:
1) Найти значение производной функции у=f(x), заданной на отрезке [a, b] с помощью многочлена Лагранжа (n=4) в точке x=m. Сравнить полученный результат с точным значением производной в точке, используя непосредственное дифференцирование функции.
2) Найти значение производной функции у=f(x), заданной на отрезке [a, b] с помощью многочлена Ньютона (n=5) в точке x=a. Оценить погрешность.
Варианты заданий к лабораторной работе № 11
№ 1 № 2
, а=1,5, b=2, m=1,55. 
, а=1,5, b=2, m=1,55.
№ 3 № 4
, а=2, b=2,5, m=2,06. , а=2, b=2,5, m=2,06.
№ 5 № 6
, а=2, b=2,5, m=2,04. 
, а=3, b=3,5, m=3,03.
№ 7 № 8
, а=70, b=90, m=73. , а=4,5, b=10, m=5,03.
№ 9 № 10
, а=3,4, b=4,3, m=3,6. , а=0,5, b=1,5, m=0,63.
№ 11 № 12
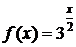, а=5,4, b=6, m=5,6. 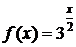, а=6, b=7,5, m=6,12.
№ 13 № 14
, а=3, b=6, m=3,04. , а=5, b=7, m=5,03.
№ 15 № 16
, а=0, b=1, m=0,06. , а=0, b=1, m=0,06.
Глава 6. Численное интегрирование
Справочные материалы по численному интегрированию
Квадратурные формулы Ньютона - Котеса
В тех случаях, когда для вычисления определённого интеграла 
по каким-либо причинам не представляется возможным использовать формулу Ньютона - Лейбница, применяют численные методы вычисления интеграла. Многие из них основаны на том, что на отрезке [a, b] функцию f(x) заменяют интерполирующей функцией.
Разобьём отрезок интерполирования [a, b] на п частей. Получим 
точку 
, где 
. Заменим функцию f(x) на отрезке [a; b] интерполяционным многочленом Лагранжа для равноотстоящих узлов. Обозначим значения функции в узлах интерполяции: 
.
|
|
|
,
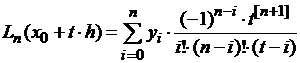где 
.
Положим:
Сделаем замену: 
, 
.
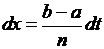При 
имеем t = 0, а при 
имеем t = n. Получаем:
(6.1)
где 
(6.2)
Формула (6.1) называется квадратурной формулой Ньютона - Котеса, а (6.2) называются коэффициентами Котеса.
Формула трапеций
При 
из формулы (6.1), (6.2) получаем:
(6.3)
Формула (6.3) даёт один из простейших способов вычисления определённого интеграла и называется формулой трапеций. Распространяя формулу (6.3) на все отрезки разбиения, получим общую формулу трапеций на отрезке [a; b]:
(6.4)
Оценка погрешности метода трапеции:
, где 
(6.5)
Формула Симпсона
При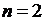 
из формул (6.1), (6.2) имеем: 
.
Получаем на отрезке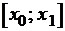 
:
(6.6)
Если 
, то применяя формулу (6.6) к каждой паре частичных отрезков 
(i = 1, 2, …m) получим:
Формула (6.7) называется формулой Симпсона.
Оценка погрешности формулы Симпсона:
, где 
.
Иногда удобно использовать следующую оценку: 
, где 
– значения интеграла, вычисленные по формуле Симпсона соответственно при п и 2п отрезках разбиения.
Пример 6.1. Вычислить интеграл: 
по формуле трапеций, разделив отрезок [0; 1] на 5 равных частей и оценить погрешность вычислений. Значения подынтегральной функции приведены в таблице:
|
|
|
| 
| 
|
| 0,0 0,2 0,4 0,6 0,8 1,0 | 0 0,4207355 | 0,0079467 0,0623068 0,2032711 0,4591078 |
| Σ | 0,4207355 | 0,7326324 |
I=0,2ּ(0,4207355+0,7326324)=0,2306736.
Оценка ошибки метода: На отрезке [0; 1] 
. Получаем 
.
Пример 6.2. Вычислить интеграл: по формуле Симпсона, разделив отрезок [0; 1] на 10 равных частей и оценить погрешность вычислений. Значения подынтегральной функции приведены в таблице 6.1.
.
Для оценки остаточного члена найдём производную четвёртого порядка от подынтегральной функции.
Таблица 6.1
Значения функции для примера 6.1.
Дата добавления: 2018-06-01; просмотров: 1079; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!