Комбинированный метод хорд и касательных
Комбинированный метод основан на одновременном использовании методов хорд и касательных.
В результате получим две монотонные последовательности {xп}, {x'п}- приближенные значения корня по недостатку и по избытку соответственно.. Для нахождения корня ξ с заданной степенью точности достаточно ограничится теми значениями 
, для которых 
. Так как 
, то в качестве значения корня следует взять среднее арифметическое чисел 
, т. е. число 
. Легко видеть, что 
.
Расчётные формулы:
а) если 
на [a; b], то:
.
б) если 
на [a; b], то:
.
Пример 2.1.Дано уравнение 
. Исследовать вопрос о существовании и единственности корня ξ на отрезке [0,5; 1,5]. Вычислить три приближения корня уравнения по методу хорд и по методу касательных.
Вычисляем знак выражения 
, где 
. Т. к. 
и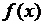 
непрерывная функция на отрезке [0,5; 1,5], то уравнение имеет хотя бы один корень на заданном отрезке.
1. Для доказательства единственности корня вычисляем f '(x), f ''(x) и определим их знак на отрезке [0,5; 1,5].
, 
, f''(x)>0 на отрезке [0; 1], следовательно, f(x) монотонно возрастает, и корень уравнения на отрезке [0; 1] единственный; 
, следовательно, функция сохраняет на отрезке выпуклость. Т.к. 
, то для вычисления приближенных значений корня по методу хорд используются формулы (2.3), а по методу касательных (2.7).
Используя данные формулы, получаем ответ:
– приближенные значения корня по методу хорд; 
– приближенные значения корня по методу касательных.
|
|
|
Метод простой итерации
Для использования этого метода исходное нелинейное уравнение записывается в виде
. (2.8)
Пусть известно начальное приближение корня x=x0
Подставляя это значение в правую часть уравнения (2.8), получаем новое приближение: c1=f(c0). Подставляя каждый раз новое значение корня в правую часть уравнения (2.8), получаем последовательность значений:
, 
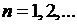(2.9)
Итерационный процесс прекращается, если результаты двух последовательных итераций близки 
.
Достаточным условием сходимости метода простой итерации является условие 
на множестве действительных чисел.
Достаточным условием сходимости метода простой итерации на отрезке [a; b] является условие , 
[a; b].
Для более точной оценки погрешности используются формулы:
,
где 
, на множестве [a; b].
Пример 2.2. Вычислить четыре приближения методом простой итерации для уравнения 
.
Для исследования выберем отрезок [0; 3].
1) Функция 
определена и имеет в каждой точке x из отрезка [0; 3] производную: 
.
2) Значения функции удовлетворяют неравенству:
, т. е. все значения функции содержатся в отрезке [0; 3].
3) Производная функции удовлетворяет неравенству:
|
|
|
, т. е. существует 
такое, что для всех x из отрезка [0; 3] имеет место неравенство: 
. Следовательно, выполнено достаточное условие применимости метода простой итерации на отрезке.
Выберем произвольно 
из отрезка [0; 3], например 
. Используя формулу (2.9), получаем четыре приближенных значения корня:
Оценим погрешность четвертого приближения:
.
Дата добавления: 2018-06-01; просмотров: 631; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!