Метод Зейделя для систем линейных уравнений
Метод Зейделя является модификацией метода простой итерации. Вычисление 
проводится по следующим формулам:
Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.
Пример 3.2. Рассмотрим вычисление двух приближений по методу Зейделя для примера, решенного выше для метода простой итерации и оценим погрешность.
Вычисления будем проводить по формулам:
Выбираем начальное приближение: 
и получаем:
, 
.
.
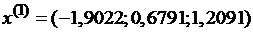Метод Ньютона для систем нелинейных уравнений.
Пусть дана система:
Согласно методу Ньютона последовательные приближения вычисляются по формулам:
,
где 
Начальные приближения 
определяются приближенно (например, графически).
Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.
Пример 3.3. Найти одно приближение для решения системы. За начальное приближение системы принять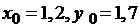 
.
.
Вычисляем в начальной точке :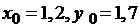
.
Получаем первые приближения:
.
Лабораторная работа № 5 Решение систем линейных уравнений методом Гаусса. Вычисление обратной матрицы
Задания:
1) Решить заданную систему уравнений методом Гаусса с выбором главного элемента.
2) Вычислить для матрицы A обратную матрицу A-1, используя метод Гаусса. Матрица A задается системой уравнений 
.
Варианты заданий к лабораторной работе № 5
|
|
|
№1 №2
№3 №4
№3 №4
№5 №6
№7 №8
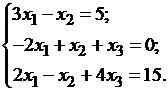
№9 №10
№11 №12
№13 №14
№15 №16
Лабораторная работа №6 Решение систем линейных уравнений методом простой итерации и методом Зейделя
Задания: Дана система линейных уравнений .
1) Привести систему линейных уравнений к итерационному виду.
2) Исследовать итерационную последовательность на сходимость.
3) Найти решение системы линейных уравнений методом простой итерации с точностью до e = 0,00001.
4) Найти решение системы линейных уравнений методом Зейделя. с точностью до e = 0,00001.
Варианты заданий к лабораторной работе № 6
№ 1.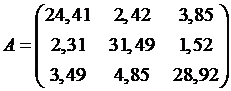 
, 
.
№ 2. 
, 
.
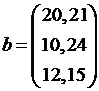№ 3. 
, 
.
№ 4.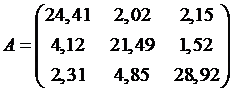 
, 
.
№ 5 
, 
.
№ 6.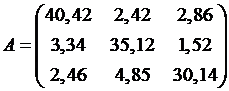 
, 
.
№ 7. 
, 
.
№ 8. 
, 
.
№ 9. 
, 
.
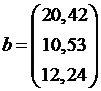№ 10. 
, 
.
№ 11. 
, 
.
№ 12. 
, 
.
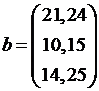№ 13. 
, 
.
№ 14. 
, 
.
№ 15. 
, 
.
№ 16. 
, 
.
Лабораторная работа № 7 Решение систем нелинейных уравнений методом Ньютона
Задание:
Решить систему уравнений с помощью метода Ньютона. Результаты получить с пятью верными знаками. Начальные приближения найти графически.
Варианты заданий к лабораторной работе № 7
№ 1.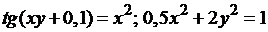 
.
№ 2. 
.
№ 3. 
.
№ 4. 
.
№ 5. 
.
№ 6.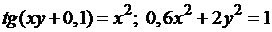 
.
№ 7.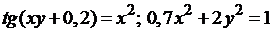 
.
№ 8. 
.
№ 9. 
.
№ 10. 
.
№ 11 
№ 12 
.
№ 13. 
.
№ 13. 
.
№ 14. 
.
№ 15. 
.
№ 16. 
Глава 4. Численное интерполирование
|
|
|
Справочный материал по численному интерполированию
4.1.1. Постановка задачи численного интерполирования
Пусть на отрезке [а; b] заданы точки 
, которые называются узлами интерполяции. Будем предполагать, что все точки 
различны и расположены в порядке возрастания.
Пусть известны значения некоторой функции 
в этих точках:
. (4.1)
Требуется в определенном классе функций построить такую функцию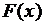 
, значения которой в узлах интерполяции совпадают со значениями 
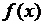. Функцию 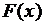будем называть интерполирующей функцией.
Будем искать интерполирующую функцию 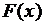в виде интерполяционного многочлена n-й степени:
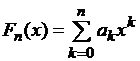. (4.2)
Условия (4.1) в данном случае перепишутся:
(4.3)
Коэффициенты многочлена (4.2) 
находятся единственным образом из условий (4.3). Рассмотрим различные способы записи интерполяционного многочлена.
Дата добавления: 2018-06-01; просмотров: 1295; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!