Лабораторная работа №2 Графический и аналитический способы отделения корней нелинейного уравнения. Уточнение корней методом половинного деления.
Задания:
1) Исследовать уравнение f(x)=0 на отрезке [a; b] на существование и единственность корня, используя аналитический и графический методы.
2) Вычислить три приближения корня методом половинного деления и оценить погрешность последнего приближения.
Варианты заданий к лабораторной работе № 2
№ 1. 
№ 2. 
№ 3. 
№ 4.  .
.
№ 5.  .
.
№ 6.  .
.
№ 7.  .
.
№ 8.  .
.
№ 9.  .
.
№ 10.  .
.
№ 11.  .
.
№ 12.  .
.
№ 13.  .
.
№ 14.  .
.
№ 15.  .
.
№ 16.  .
.
Лабораторная работа № 3 Решение нелинейных уравнений методами хорд, касательных, комбинированным методом хорд и касательных
Задания:
1) Найти три приближения корня для уравнения f(x)=0 на отрезке [a; b] а) методом хорд; б) методом касательных. Вычислить погрешность третьего приближения для каждого метода.
2) Найти приближенный корень уравнения корень уравнения 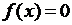 на отрезке [a; b] с точностью до
на отрезке [a; b] с точностью до  комбинированным методом хорд и касательных.
комбинированным методом хорд и касательных.
Использовать варианты заданий для лабораторной работы № 2.
Лабораторная работа № 4 Метод простой итерации для нелинейных уравнений
Задание:
Методом простой итерации вычислить корень уравнения с точностью до  . Отрезок, на котором корень существует и единственный, выделить самостоятельно.
. Отрезок, на котором корень существует и единственный, выделить самостоятельно.
Варианты заданий к лабораторной работе № 4
№ 1.  . № 2.
. № 2.  .
.
№ 3.  . № 4.
. № 4.  .
.
№ 5.  . № 6.
. № 6.  .
.
№ 7.  . № 8.
. № 8.  .
.
№ 9.  . № 10.
. № 10.  .
.
|
|
|
№ 11.  . № 12.
. № 12. 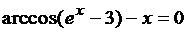 .
.
№ 13.  . № 14.
. № 14.  .
.
№ 15.  . № 16.
. № 16.  .
.
Глава 3. Решение систем линейных и нелинейных уравнений
Справочный материал по численным методам решений систем линейных уравнений
Метод Гаусса с выбором главного элемента для системы линейных уравнений
Система из п линейных уравнений с п неизвестными вида:
 (3.1)
(3.1)
имеет единственное решение при условии: 
 , где
, где
 матрица коэффициентов
матрица коэффициентов  системы (3.1)
системы (3.1)
К точным методам относится метод Гаусса с выбором главного элемента. Среди элементов  матрицы А выберем наибольший по модулю, называемый главным элементом. Пусть им будет элемент
матрицы А выберем наибольший по модулю, называемый главным элементом. Пусть им будет элемент  . Строка с номером р, содержащая главный элемент, называется главной строкой. Далее вычисляем множители:
. Строка с номером р, содержащая главный элемент, называется главной строкой. Далее вычисляем множители:  для всех
для всех  . Затем преобразуем матрицу следующим образом: из каждой неглавной строки вычитаем почленно главную строку, умноженную на mi . В результате получим матрицу, у которой все элементы q-го столбца, за исключением
. Затем преобразуем матрицу следующим образом: из каждой неглавной строки вычитаем почленно главную строку, умноженную на mi . В результате получим матрицу, у которой все элементы q-го столбца, за исключением  , равны нулю. Отбрасываем этот столбец и главную строку и получаем новую матрицу
, равны нулю. Отбрасываем этот столбец и главную строку и получаем новую матрицу  с меньшим на единицу числом строк и столбцов. Над матрицей
с меньшим на единицу числом строк и столбцов. Над матрицей  повторяем аналогичные операции, после чего получаем матрицу А2 и т. д.
повторяем аналогичные операции, после чего получаем матрицу А2 и т. д.
|
|
|
Такие преобразования продолжаем до тех пор, пока не получим матрицу, содержащую одну строку, которую считаем тоже главной. Затем объединяем все главные строки, начиная с последней. После некоторой перестановки они образуют треугольную матрицу, эквивалентную исходной. На этом заканчивается этап вычислений, называемый прямым ходом. Решив систему с полученной треугольной матрицей коэффициентов, найдём последовательно значения неизвестных  . Этот этап вычислений называется обратным ходом.
. Этот этап вычислений называется обратным ходом.
Смысл выбора главного элемента состоит в том, чтобы сделать достаточно малым число mi и тем самым уменьшить погрешность вычислений.
Дата добавления: 2018-06-01; просмотров: 1297; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
