Функциональные ряды.
Пример: x+x в квадрате/2+ x в кубе/3+х в 4-й степени/4+….и т.д.= 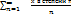
Sinx+sin2x+sin3x+…= 
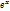 -
- 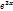 +
+ 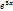 -
- 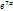 +
+ 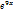 -….=
-….= 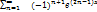
2n-четные
Функциональные ряды- последовательность, функций вместе с фиксированным порядком их суммирования.
Обозначение: 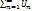 (x)=
(x)= 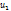 (x)+
(x)+ 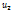 (x)+
(x)+  (x)+ и т.д.
(x)+ и т.д.
Пример: Рассмотрим ряд 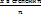
А)Если подставить в этот ряд х=1 получим:
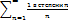 =1+
=1+  +
+  +
+  и т.д.- гармонический ряд расходится потому что:
и т.д.- гармонический ряд расходится потому что:
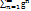 -сумма геометр.прогрессии,
-сумма геометр.прогрессии, 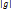 <1-сходится,
<1-сходится, 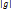 >=1-расходится
>=1-расходится
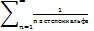 -огр альфа больше 1-сходится, альфа меньше или равно 1-расходится
-огр альфа больше 1-сходится, альфа меньше или равно 1-расходится
Б) Если х=-1, то 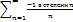 =-1+
=-1+  -
-  +
+ 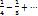 ряд знакочередующийся
ряд знакочередующийся
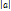 убывает,
убывает, 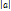 стремится к 0, при n, стремящемся к бесконечности, сл-но это ряд Лейбница, поэтому сходится
стремится к 0, при n, стремящемся к бесконечности, сл-но это ряд Лейбница, поэтому сходится
Если будет + - то расходится
Данный ряд Сходится условно, т.к. сумма эта большая Е 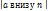 -расходится
-расходится
Пусть х=  , тогда
, тогда 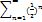 *
*  =
= 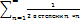 =
=  +
+ 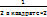 +
+ 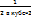 ……
……
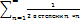 <
< 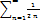 - сходится, т.к. из сходимости большего следует сход-ть меньшего. Тогда исследуемый ряд сходится так же по 1 признаку сравнения.
- сходится, т.к. из сходимости большего следует сход-ть меньшего. Тогда исследуемый ряд сходится так же по 1 признаку сравнения.
Х=2, тогда 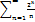 = 2+
= 2+  +
+  +
+  +…
+…
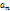 стремится к бесконечности при n стремящемся к 0. Не выполняется необходимый признак сходимости ряда, следовательно ряд расходится.
стремится к бесконечности при n стремящемся к 0. Не выполняется необходимый признак сходимости ряда, следовательно ряд расходится.
Примечание: подставляем в функциональный ряд 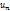 (x) конкретные значения аргумента от х=
(x) конкретные значения аргумента от х= 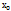 будем получать конкретные числовые ряды, которые могут быть знакоположительными и знакопеременными. Первые могут как сходиться так и расходиться, вторые же - могут сходиться как условно, так и абсолютно.
будем получать конкретные числовые ряды, которые могут быть знакоположительными и знакопеременными. Первые могут как сходиться так и расходиться, вторые же - могут сходиться как условно, так и абсолютно.
Определение: Множество всех точек (значениях х), в которых сходится функциональный ряд 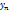 от х называется ОБЛАСТЬЮ СХОДИМОСТИ ФУНКЦИОНАЛЬНОГО РЯДА.
от х называется ОБЛАСТЬЮ СХОДИМОСТИ ФУНКЦИОНАЛЬНОГО РЯДА.
Х-область сходимости функционального ряда.
Алгоритм исследования функционального ряда на сходимость:
1. Фиксируем х. Рассматриваем ряд 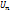 (x) как числовой.
(x) как числовой.
2. Поиск условия сходимости. Рассматривается ряд, т.е. исследуем на сходимость, используя признаки сходимости знакоположительных рядов (Даламбер, Коши, признаки сходимости)
3. Определение интервала сходимости и исследование поведения ряда на границах интервала.
4. Запись области сходимости с учетом граничных точек.
Пример: исследуем на сходимость 
1)Пусть х - фиксированное число, при подстановке этого числа, функциональный ряд превратиться в числовой. Очевидно, что при различных х ряд может оказаться и знакополож. И знакопеременным. Поэтому исследуем его сначала на абсолютную сходимость.
2)  =
= 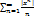 знакоположительный, если
знакоположительный, если 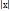 >1, то
>1, то  =
= 
След-но ряд расходится, т.к. не выполняется необходимый признак сходимости ряда.
Если модуль по х меньше 1, то сравниваем 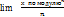 меньше чем
меньше чем 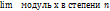 как сумма гометр.прогрессии модуль g меньше 1.
как сумма гометр.прогрессии модуль g меньше 1.
По 1-му признаку сравнения из сходимости меньшего следует сходимость большего, значит ряд сходится абсолютно.
3) Интервал сходимости в точках от -1 до 1 ряд сходиться абсолютно. От бесконечности до -1 и от 1 до бесконечности ряд расходится.
Исследуем поведение ряда на границах интервала сходимости
Х=1 сумма вверху бесконечности внизу n=1 1/n-расходится, гармонический ряд
Х=-1 такая же сумма (-1) в степени n/n-ряд Лейбница, сходится. По модулю этот ряд будет расходится, а сл-но сумма по модулю -1 сходится условно
В итоге область сходимости ряда от квадратн.скобка -1 до 1).
12.Степенной ряд, свойства степенных рядов. Место для формулы.
Степенной ряд называют ряд вида  a n ( 𝞴-𝞴0 ) n г де
a n ( 𝞴-𝞴0 ) n г де 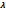 0= const, (an) – числовая последовательность.
0= const, (an) – числовая последовательность.
Пример: 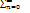
 𝞴 n / n! = 1+ x + x2/ 2! + x3/ 3!
𝞴 n / n! = 1+ x + x2/ 2! + x3/ 3!
0!=1 1!=1
 (𝞴-2)n / n2 = x-2 + (x-2)2/ 4 +(x-2)3/ 0+
(𝞴-2)n / n2 = x-2 + (x-2)2/ 4 +(x-2)3/ 0+
Центр и радиус сходимости степенного ряда.
Прим: Интервал сходимости степенного ряда всегда симметричен относительно точки 𝞴0 называют центром степенного ряда.
𝞴0
𝞴0 – центр степенного ряда
R –радиус интервала сходимости
Вывод формулы R сходимости степенного ряда.
1шаг: Рассмотрим ряд с нулевым центром  anxn
anxn
Исследуем этот ряд на абсолютную сходимость по признаку Даламбера
d= 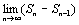 |un+1()/ un(𝞴)|=
|un+1()/ un(𝞴)|= 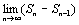 an+1 𝞴N+1/anxn =
an+1 𝞴N+1/anxn = 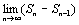 |an+1*xn*x/ an xn| = |x|
|an+1*xn*x/ an xn| = |x| 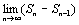 |an+1/ an |
|an+1/ an |
Условия сходимости: d < 1
|x| 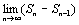 |an+1/ an |< 1
|an+1/ an |< 1
|x|< 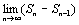 |an/ an+1| =>R
|an/ an+1| =>R
Интервал сходимости.
- R 0 R
Где R = 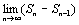 |an+1/ an |
|an+1/ an |
2 шаг: Рассмотрим произвольную центром 𝞴0
 an (𝞴-𝞴0)n
an (𝞴-𝞴0)n
Обозначим t= (𝞴-𝞴0)n , тогда  an (x-x0)n=
an (x-x0)n=  antn этот ряд сходится на интервале |t| <R, где R вычисляем по формуле (*) (R>
antn этот ряд сходится на интервале |t| <R, где R вычисляем по формуле (*) (R> 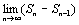 |an/ an+1|)
|an/ an+1|)
-R <t<R
-R < 𝞴- x0<R
𝞴0 – R< 𝞴<R+ 𝞴0 или | x-x0|<R
Вывод: интервал сходимости степенного ряда представляет собой окрестность точки 𝞴0 радиуса R где R вычисляется по формулам
(*) R= 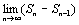 |an/ an+1| - следствие признака Даламбера
|an/ an+1| - следствие признака Даламбера
(*) R= 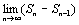 | 1/
| 1/ 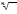 |an| - следствие признака Каши
|an| - следствие признака Каши
Дата добавления: 2015-12-21; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
