Критерий сходимости знакоположительных рядов.
Чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
Доказательство: Если ряд знакоположительный, то последовательность его частичных сумм возрастает.
Необходимо: по условию ∑Аn сходится т.е.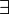 
(существует или найдется)lim Sn = S и (Sn) возрастает, тогда 
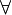n Sn < S → (Sn) ограничена.
S1 S2 S3 S
Достаточность: 1) по условию (Sn) ограничена сверху. 2) (Sn) возрастает (Sn) сходится → 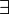lim Sn = S
Если последовательность возрастает и ограничена сверху, то по теореме Вейерштрапса она сходится.
Примечание: достаточные признаки сходимости знакоположительных рядов являются следствиями этого критерия.
Признак сравнения.
Пусть даны два знакоположительных ряда ∑Аn и ∑Вn для которых выполняется условие
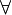n Аn≤Вn, тогда: 1) если Вn – сходится →Аn – сходится (из сходимости большего ряда следует сходимость меньшего ряда). 2) из расходимости меньшего ряда следует расходимость большего.
Доказательство: 1) по условию ∑Вn- сходится → 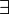lim Bn = B 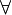n An ≤ Bn, тогда 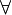n An ≤ Bn < В → (Аn) ограничена сверху числом В, а по критерию → ∑An – сходится.
2) если ∑Вn- сходится, то ∑An – сходится → ∑An – расходится, то ∑Вn – не может сходится.
Пример: ∑2n/3n+5 исследуем на сходимость.
∑(2/3)n- сходится, т.к. сумма геометрической прогрессии, |q| = 2/3 < 1. 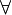n (2/3)n > 2n/3n+5?, тогда по 1 признаку сравнения ∑2n/3n+5 – сходится.
|
|
|
Признак сравнения.
Если для знакоположительных рядов ∑Аn и ∑Вn существует lim An/Bn, то ряды ведут себя одинаково (т.е. или оба сходятся или оба расходятся).
Пример: ∑2n/3n+5 – исследуем.
Сравним с ∑(2/3)n – сходится как сумма геометрической прогрессии по |q| < 1.
lim (2n/3n+5: (2/3)n) = lim 2n *3n /(3n+5) * 2n = lim 3n /3n +5|:3n = lim 1/1+(5/3n) = 1 → ряды ведут себя одинаково и данный ряд тоже сходится.
Дата добавления: 2015-12-21; просмотров: 75; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!