Теорема 3.2 (необходимое условие экстремума).

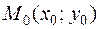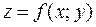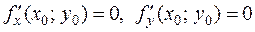Если точка является точкой экстремума функции , то или хотя бы одна из этих производных не существует.

Геометрический смысл: равенства 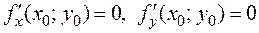означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию 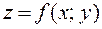, параллельная плоскости Oxy, т.к. уравнение касательной плоскости есть .

Определение 3.6. Точки, в которых хотя бы одна частная производная равна нулю или не существует, то такие точки называются критическими точками.

Если речь идет о точках, в которых частные производные первого порядка равны нулю, то такие точки называются стационарными точками.

Теорема 3.3 (достаточное условие экстремума). Пусть функция 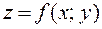имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку 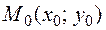. Вычислим в точке значения . Обозначим

.

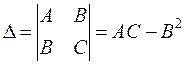Тогда:

1. если 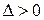, то функция 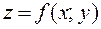имеет экстремум в точке :

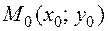§ максимум, если ;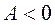

§ минимум, если ;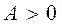

2. если 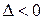, то функция 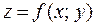не имеет экстремума в точке ;

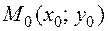3. если 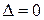, то экстремум в точке 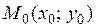может быть, а может и не быть. Необходимы дополнительные исследования.

Дата добавления: 2015-12-18; просмотров: 14; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 9 10 11 12 13 14 15 16 1718

Мы поможем в написании ваших работ!