Предел функции нескольких переменных в точке и его свойства.

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывность, аналогично случаю функции одной переменной.

Введем понятие окрестности точки.

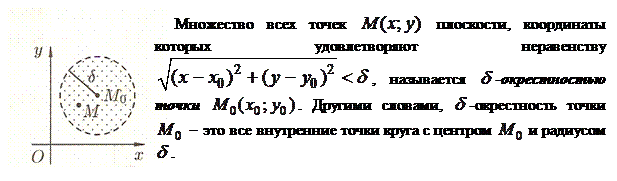
Пусть функция 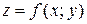определена в некоторой окрестности точки 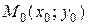, кроме, может быть, самой этой точки.

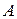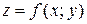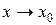Определение 1. Число называется пределом функции при и 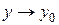(или, что то же самое, при 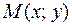® 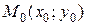), если для любого 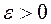существует 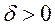такое, что для всех 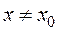и 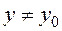и, удовлетворяющих неравенству 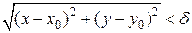, выполняется неравенство 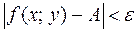. Записывают:

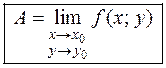(1.1)

или

.

 

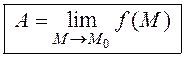Из определения следует, что если предел существует, то он не зависит от пути, по которому 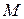стремится к 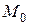(число таких направлений бесконечно). Определения бесконечно малых и бесконечно больших величин являющихся функциями двух переменных, аналогичны соответствующим определениям для функций одной переменной.

 

 

Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число 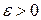, найдется -окрестность точки 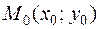, что во всех точках 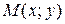, отличных от 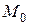, аппликаты соответствующих точек поверхности 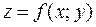отличаются от числа 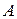по модулю меньше, чем на .

 

 

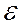№18. Непрерывность функции нескольких переменных. Свойства непрерывных функций.

Z=f(P)- определённая на D, P₀ 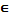D и является его предельной точкой.

Опр.1. Ф- я Z=f(P) назыв. переменной в т.F₀, если lim (P-> P₀) f(P)= f(P₀).

Если ф-я Z=f(P) непрерывна в каждой точке мн- ва D, то она непр. на мн- ве D.

Замечание. Если ф- я непр. в т. Р, то знак ф-и и знак предела можно менять местами

lim (P-> P₀)f(P)= f(lim (P->P₀) P). В точках, в к-ых ф-я не явл. непрерывной называют точками разрыва ф-ции.

Пример. Z=

9x²-4y²=0

(3x-2y)(3x+2y)=0. система:

3x-2y=0

3x+2y=0.

Рассмотрим z= f(x₁, x₂,…,x_n)

Пусть P₀(x₁⁰, x₂⁰,…,x_n⁰)

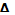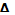Опр.2. Полным приращением ф-и f(x₁, x₂,…,x_n) в точке Р₀ соответствующим приращением x₁, x₂,…, 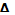x_n независимых переменных назыв. 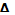Z= f(x₁⁰+ 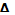x₁, x₂⁰+ 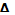x₂,…,x_n⁰+ 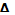x_n)- f(x₁⁰, x₂⁰,…,x_n⁰)- полное приращение.

Т|| Ф-я z= f(x₁, x₂,…,x_n) непрерывна в т. 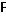₀ , тогда и только тогда, когда lim( 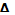x₁->0,…, 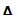x_n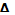->0) Z=0

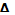. x₁⁰+ 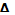x₁=x₁ …

x_n⁰+ 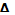x_n=x_n

P(x₁,…, x_n)

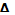Z=f(P)-f(P₀)

Для ф-и нескольких переменных можно определить понятие непрерывности по одной из переменных.

Z=(x,y) P₀(x₀, y₀)

Пусть y= cos t= y₀, тогда 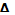_x Z= f(x₀+ 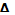x,y)-f(x₀,y₀) частное приращение ф-и Z=f(x,y) в т. Р₀ по переменной x.

Аналогично 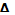_y Z= f(x₀, y₀+ 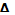y)- f(x₀,y₀)- частное приращение по y.

Опр.3. Ф-я Z=f(x,y)- непрерывная по переменной X в т. Р₀, если предел lim(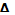 x->0) 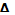_x Z=0. Аналогично по y, lim( 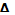y->0) 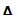_y Z=0.

Из непрерывности ф-и Z=f(x,y) в т. Р₀ следует её непрерывность по каждой из переменных. Обратное неверно.

Пример. Z= 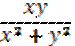, O(0,0)

Ф- я не явл. непр. в этой точке по каждой из перем. X и Y. непр. по X:Y=0.

Св-ва непрерывных ф-й:

1. f(P), g(P)- непрерывные в т. Р.

f(P) 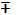g(P), f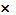(P) g(P), 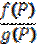(g(P)≠0)- являются непрерывными в т. Р₀.

2. Непрерывность сложной ф-и Z=f(x,y) непрерывна в т. Р₀(x₀, y₀) и система:

x= φ(t₁, t₂) φ(t₁⁰, t₂⁰)= y₀;

y= ω(t₁,t₂), где ω(t₁⁰,t₂⁰)=x₀.

И ф-и φ и ω непрерывны в М₀(t₁⁰, t₂⁰), тогда сложная ф-я z=f(φ(t₁, t₂), ω (t₁, t₂))=g(t₁, t₂) непрерывна М₀

3. Если ф-я z=f(P) непр. в т. Р₀, и f(P₀) 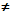0, то существует такая окрестность Р₀, в к-ой ф-я f(P) не обращается в 0.

4. Теорема Вейерштрасса: Если ф-я f(P) непрерывна на огран. Замкнутом мн-ве D, то она достигает на этом мн-ве своего наибольшего\наименьшего М, m - значений.

5. Если f(P) - непр. на огран. замкнутом мн- ве, то она принимает на этом мн- ве любое значение заключ. между m и M.

 

 

 

 

---

Дата добавления: 2015-12-18; просмотров: 19; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!