Формула Тейлора для функции нескольких переменных.

Если функция z = f(x,y) непрерывна вместе со своими частными производными до (n + 1)-го порядка включительно в точке (x₀,y₀) и в некоторой её окрестности, то можно показать, что такая функция представима в виде суммы многочлена n -й степени относительно (x-x₀) и (y-y₀) и некоторого остаточного члена.

В случае n = 2 это представление будет выглядеть следующим образом:

f(x,y)=F+D(x-x₀)+E(y-y₀)+A(x-x₀)²+B(x-x₀)(y-y₀)+C(y-y₀)²+R₂ (1)

где A, B, C, D, E, F – числа, R₂ – остаточный член.

Исходной для вывода формулы (1) является формула Тейлора второго порядка для функции одной переменной:

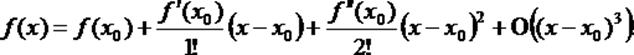
Запишем эту формулу для функции f (x,y), считая пока аргумент y постоянным:

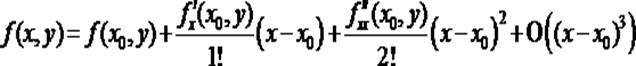(2)

Теперь записываем по формуле Тейлора функции, зависящие только от у:

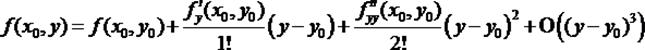
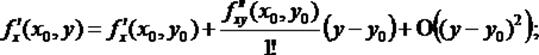
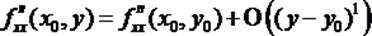
Сделаем подстановку этих функций в равенство (2):

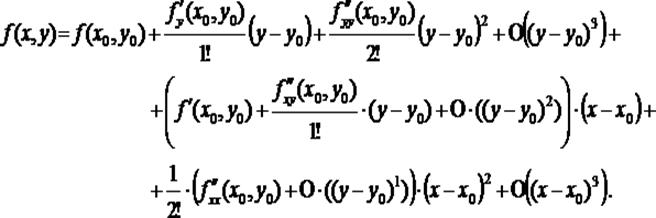
Расположим слагаемые в порядке возрастания степеней (x – x₀) и (y – y₀):

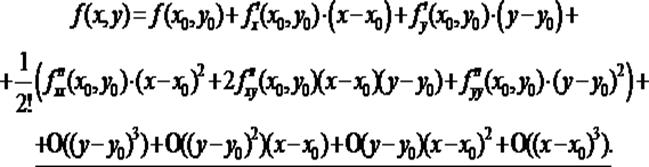
Здесь последние выделенные слагаемые составляют остаточный член R2(x,y), они имеют порядок малости 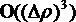, где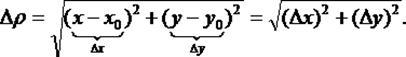

 

Таким образом, формула Тейлора второго порядка для функций двух переменных имеет вид:

 

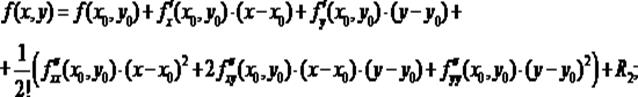(3)

 

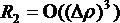-это остаточный член формулы Тейлора второго порядка, величина которого имеет одинаковый порядок малости с .

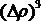Из формулы (3) следует, что в некоторой малой окрестности точки (x₀;y₀) остаточным членом R₂ можно пренебречь вследствие его малости и записать приближенное выражение функции f(x,y) в виде многочлена второй степени по разностям (x-x₀) и (y-y₀):

 

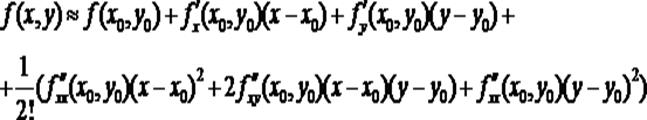(4)

 

Выражение в правой части формулы (4) называется многочленом Тейлора второй степени, соответствующим функции f(x,y). Особенно просто выглядит представление функции ее многочленом Тейлора в окрестности точки (0;0):

 

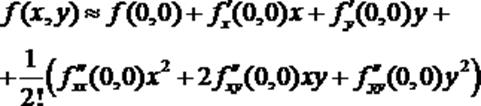(4’)

 

 

---

Дата добавления: 2015-12-18; просмотров: 43; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!