Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
Пусть функция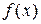 
непрерывна на отрезке 
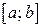. Тогда она интегрируема и на любом отрезке 
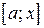, где 
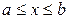, т.е. для любого 
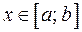имеет смысл интеграл 
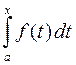. Рассмотрим функцию
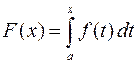, (1)
которая определена на отрезке 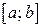и называется интегралом с переменным верхним пределом.
Выделим 2 основных св-ва этой функции:
1) 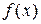непрерывна на [a,b]
2) Если функция 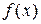непрерывна и диф-ма на отрезке 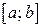, то производная функции 
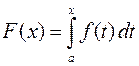существует в каждой точке 
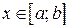, причем
.
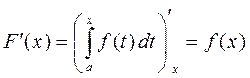Надо отметить, что любая функция 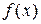, непрерывная на отрезке 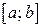, имеет первообразную, определяемую формулой (1)
Теорема 1. Если функция 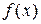непрерывна и диф-ма на отрезке 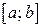, то производная функции 
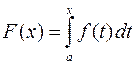существует в каждой точке 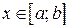, причем
.
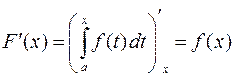Надо отметить, что любая функция 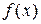, непрерывная на отрезке 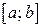, имеет первообразную, определяемую формулой (1).
Теорема (формула Ньютона-Лейбница): если функция 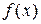непрерывна на отрезке 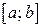и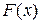 
- какая-нибудь первообразная для 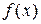на этом отрезке, то справедлива формула Ньютона-Лейбница
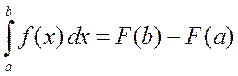. (2)
Доказательство. Рассмотрим интеграл с переменным верхним пределом
,
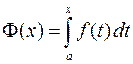где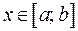 
, на котором 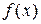непрерывна. Согласно теореме 1, 
.
Пусть 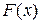- первообразная функции 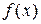, т.е. 
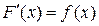. Тогда по теореме 1.1 заключаем, что
.
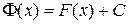При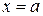 
получаем
.
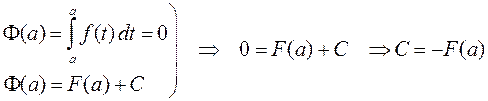Далее
,
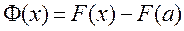или
.
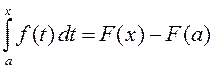При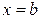 
получаем
.
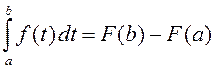По свойству о независимости переменных получаем
.
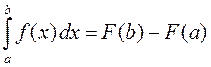Формулу Ньютона-Лейбница (2) можно записать в ви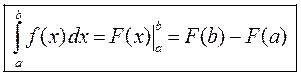де
,где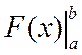 
- называется двойной подстановкой от 
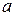до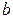 
для функции .
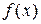Дата добавления: 2015-12-18; просмотров: 15; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!