Интегрирование по частям. Примеры
Пусть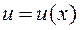 
и 
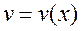- функции, имеющие непрерывные производные. Тогда 
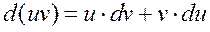. Интегрируя это равенство, получаем
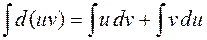
или
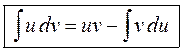. (1)
Формула (1) называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла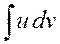 
к вычислению интеграла 
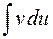, который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителе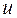й 
и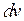 
(это, как правило, можно осуществить несколькими способами); затем, после нахождения 
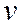и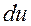 
, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Большая часть интегралов, берущихся по формуле (1), может быть разбита на три группы:
1 группа. Интегралы вида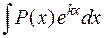 
, 
, 
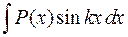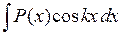, где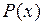 
- многочлен, 
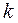- число. Удобно положить 
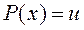, а за 
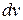обозначить все остальные сомножители.
2 группа. Интегралы вида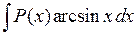 
, 
, 
, 
, 
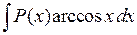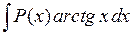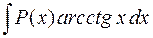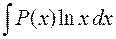. Удобно положить 
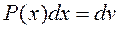, а за 
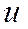обозначить остальные сомножители.
3 группа. Интегралы вида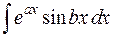 
, 
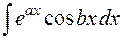, где 
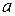и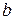 
- числа, 
, 
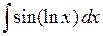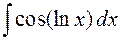. Применяя формулу (1) к любому из указанных интегралов дважды, мы получим для нахождения интеграла уравнение первого порядка, причем за 
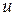можно принимать любой из сомножителей.
Конечно, указанные группы не исчерпывают всех интегралов, которые можно вычислять по формуле (1).
Пример 2.3. Найти следующие интегралы:
1) 
;
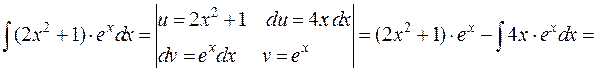
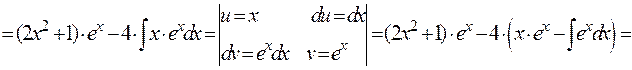
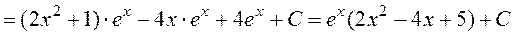2) 
;
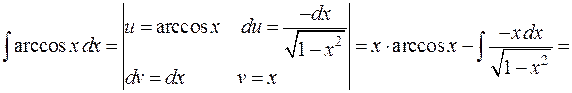
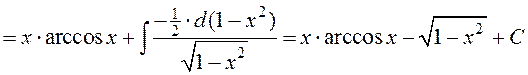3) 
.
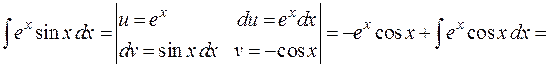
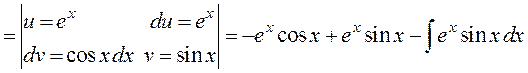Таким образом, получаем
|
|
|
.
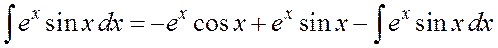Далее
,
.
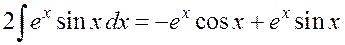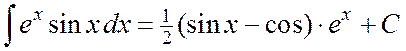5. Определённый интеграл и его геометрический смысл.
Определение 1. Определенным интегралом от функции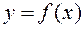 
на отрезке 
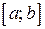называется конечный предел ее интегральной суммы, когда число частичных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл обозначается символом 
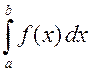. Таким образом,
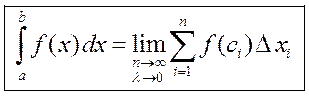. (1)
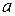Числа и 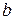называются соответственно нижним и верхним пределами интегрирования, 
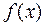- подынтегральной функцией, 
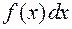- подынтегральное выражение, x - переменной интегрирования, отрезок 
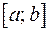- областью (отрезком) интегрирования.
Функция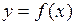 
, для которой на отрезке 
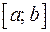существует определенный интеграл 
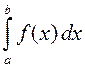, называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла (без доказательства).
Теорема 1 (теорема Коши). Если функция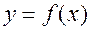 
непрерывна на отрезке 
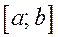, то определенный интеграл 
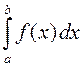существует.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечной число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения.
|
|
|
1) Определенный интеграл не зависит от обозначения переменной интегрирования:
.
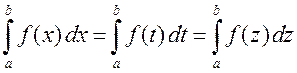2) Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
.
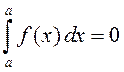3) Для любого действительного числа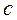 
: 
.
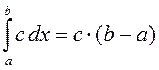Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции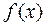 
на отрезке 
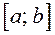численно равен площади криволинейной трапеции - фигуры, ограниченной сверху графиком функции 
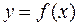, снизу – осью 
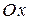, сбоку – прямым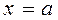и 
и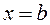 
:
.
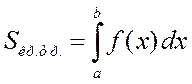Дата добавления: 2015-12-18; просмотров: 16; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!