Замена переменной в интеграле. Примеры.
Пусть требуется найти интеграл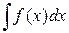 
, причем непосредственно подобрать первообразную для 
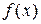мы не можем, но нам известно, что она существует.
Сделаем замену переменной в подынтегральном выражении, положив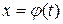 
, где 
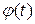- непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда 
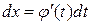и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
.
Иногда целесообразно подбирать подстановку в виде 
, тогда
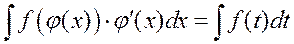, где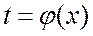 
.
Другими словами, формулу (2.1) можно применять справа налево.
Пример 2.2. Найти следующие интегралы:
1) 
;
3) 
;
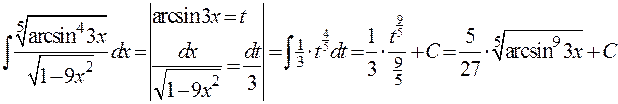Дата добавления: 2015-12-18; просмотров: 17; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!