Энергетические соотношения
2.9.1. Теорема о равенстве среднего упругого потенциала “эффективному” упругому потенциалу. В подпараграфе 1.3.3 были сформулированы и доказаны теоремы о равенстве среднего по объему упругого потенциала “эффективному” упругому потенциалу при задании кинематических или статических граничных условий Хашина – Розена. В параграфах 2.6, 2.7, 2.8 сформированы новые граничные условия, удовлетворяющие условиям кинематической и статической совместности деформированных ячеек периодичности – кинематико-статические граничные условия в задачах о поперечном растяжении и поперечном сдвиге, смешанные граничные условия в задаче о продольном сдвиге ячейки периодичности. Для новых граничных условий также имеет место
Теорема 3. Если для гетерогенной среды, занимающей объем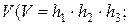 
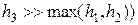и ограниченной поверхностью S
1. В задаче о поперечном растяжении (плоская деформация) заданы кинематико-статические граничные условия:
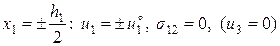; (2.9.1)
;
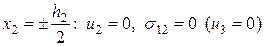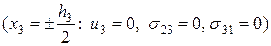
2. В задаче о поперечном сдвиге (плоская деформация) заданы кинематико-статические граничные условия:
; (2.9.2)
;
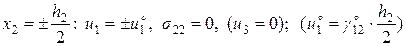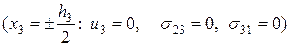
3. В задаче о продольном сдвиге (антиплоская деформация) заданы смешанные граничные условия:
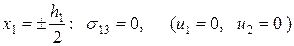; (2.9.3)
;
;
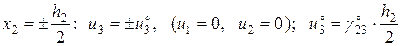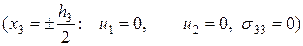соответствующие однородному напряженно-деформированному состоянию гомогенной среды, то средний по объему упругий потенциал равен “эффективному” упругому потенциалу:
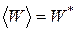(2.9.4)
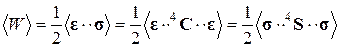(2.9.5)
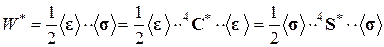(2.9.6)
а эффективные определяющие соотношения имеют вид:
|
|
|
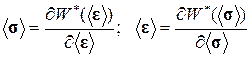(2.9.7)
2.9.2. Задача о поперечном растяжении. Докажем теорему в случае, когда на поверхности S, ограничивающей объем V, заданы кинематико-статические граничные условия (2.9.I).
1. Вычислим средний по объему 
упругий потенциал:
Учитывая граничные условия (2.9.1), получим:
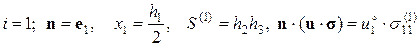
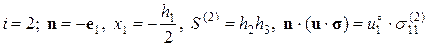
Из свойства двоякой четности нормального напряжения 
следует: 
.
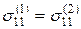Выражение для среднего по объему V упругого потенциала принимает вид:
(2.9.8)
2. Вычислим средний по объему V тензор деформаций:
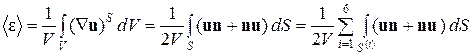
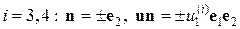
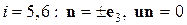
Учитывая свойства четности–нечетности компонентов вектора перемещения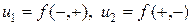 
, запишем выражение для среднего по объему тензора деформаций в следующем виде:
(2.9.9)
3. Вычислим средний по объему V тензор напряжений:
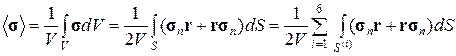
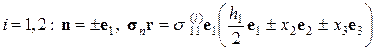
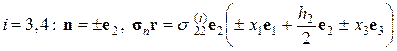
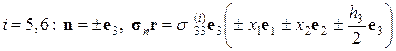
Из свойства двоякой четности нормальных напряжений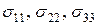 
следует:
.
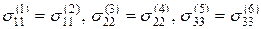Выражение для среднего по объему V тензора напряжений принимает вид:
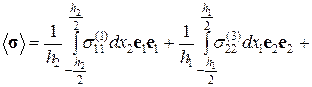
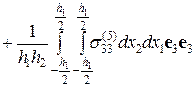(2.9.10)
4. Определим “эффективный” упругий потенциал, используя выражения (2.9.9) и (2.9.10):
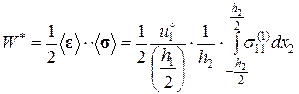(2.9.11)
Сравнив выражения (2.9.8) и (2.9.11), убеждаемся, что при задании кинематико-статических граничных условий (2.9.1) средний по объему V упругий
потенциал равен “эффективному” упругому потенциалу.
2.9.3. Задача о поперечном сдвиге. Докажем теорему в случае, когда на поверхности S, ограничивающей объем V, заданы кинематико-статические граничные условия (2.9.2).
|
|
|
1. Вычислим средний пообъему V упругий потенциал, учитывая граничные условия (2.9.2) и свойства двоякой четности касательного напряжения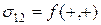 
:
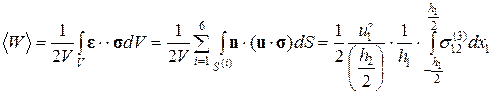(2.9.12)
2. Вычислим средний по объему V тензор деформаций, учитывая граничные условия (2.9.2) и свойства четности–нечетности компонентов вектора перемещения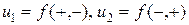 
:
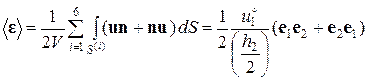(2.9.13)
3. Вычислим средний по объему V тензор напряжений, учитывая граничные условия (2.9.2) и свойства двоякой четности напряжений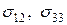 
:
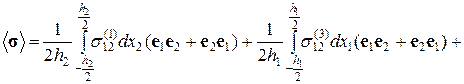
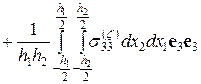
Учитывая условие обращения в нуль главного момента поверхностных сил
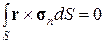
запишем выражение для среднего по объему V тензора напряжений в следующем виде:
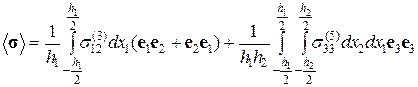(2.9.14)
4. Определим “эффективный” упругий потенциал, используя выражения (2.9.13), (2.9.14):
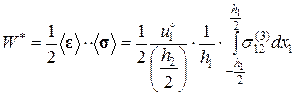(2.9.15)
Сравнив выражения (2.9.12) и (2.9.15), убеждаемся, что при задании кинематико-статических граничных условий (2.9.2) средний по объему V упругий потенциал равен “эффективному” упругому потенциалу.
2.9.4. Задача о продольном сдвиге. Докажем теорему в случае, когда на поверхности S, ограничивающей объем V, заданы смешанные граничные условия (2.9.3).
1. Вычислим средний по объему V упругий потенциал, учитывая граничные условия (2.9.З) и свойства двоякой четности касательного напряжения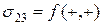 
:
|
|
|
(2.9.16)
2. Вычислим средний по объему V тензор деформаций, учитывая граничные условия (2.9.3) и свойства четности-нечетности компонента вектора перемещения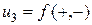 
:
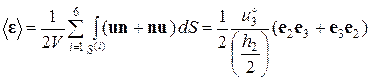(2.9.17)
3. Вычислим средний по объему V тензор напряжений, учитывая граничные условия (2.9.3) и свойства двоякой четности–нечетности касательных напряжений ,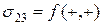 
:
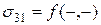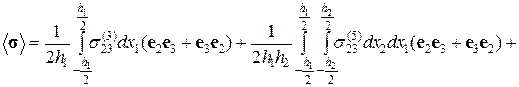
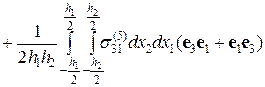
Учитывая условие обращения в нуль главного момента поверхностных сил
,
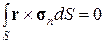запишем выражение для среднего по объему V тензора напряжений в следующем виде:
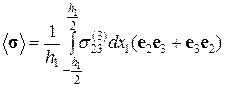(2.9.18)
4. Определим “эффективный” упругий потенциал, используя выражения (2.9.17), (2.9.18):
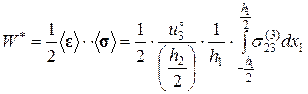(2.9.15)
Сравнив выражения (2.9.16) и (2.9.19), убеждаемся, что при задании смешанных граничных условий (2.9.3) средний по объему упругий потенциал равен “эффективному” упругому потенциалу.
Теорема доказана.
Дата добавления: 2015-12-17; просмотров: 19; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!