Определение эффективных модулей Юнга и коэффициентов Пуассона
3.1.1. Эффективные определяющие соотношения для макроскопически ортот-ропной гетерогенной среды. Эффективный модуль Юнга в направлении волокон. Рассмотрим однонаправленный волокнистый упругий композит с двоякопериодической структурой, компоненты которого идеально связаны между собой. Представительный элемент объема (ячейка периодичности) рассматриваемой гетерогенной среды изображен на рис. 2.1.
Эффективные определяющие соотношения (1.3.1) для макроскопически ортотропной гетерогенной среды имеют вид:
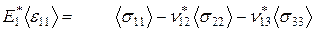
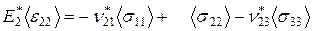 (3.1.1)
(3.1.1)

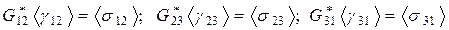
В уравнениях (3.1.1) содержится 12 эффективных упругих постоянных: 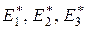 – эффективные модули Юнга;
– эффективные модули Юнга; 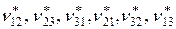 – эффективные коэффициенты Пуассона;
– эффективные коэффициенты Пуассона; 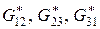 – эффективные модули сдвига; эффективные модули Юнга и коэффициенты Пуассона связаны равенствами:
– эффективные модули сдвига; эффективные модули Юнга и коэффициенты Пуассона связаны равенствами:
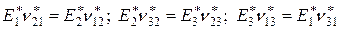 (3.1.2)
(3.1.2)
следовательно, число независимых упругих постоянных для макроскопически ортотропной гетерогенной среды – 9.
Эффективный модуль Юнга в направлении волокон 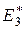 с высокой степенью точности определяется по правилу смесей [5, 6, 12, 27–31]:
с высокой степенью точности определяется по правилу смесей [5, 6, 12, 27–31]:
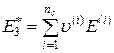 , (3.1.3)
, (3.1.3)
где nc – число компонентов композиционного материала; 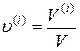 – объемная концентрация i -го компонента;
– объемная концентрация i -го компонента; 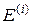 – модуль Юнга i -го компонента.
– модуль Юнга i -го компонента.
Эту формулу легко получить из условия равенства продольных деформаций в матрице и волокнах при продольном растяжении. Точное решение методами теории упругости дает практически ту же зависимость, поправка составляет доли процента [5, 6, 8, 15, 30]. Хорошее совпадение теоретической и экспериментальной зависимостей [30] позволяет рекомендовать формулу (3.1.3) для практического применения.
|
|
|
3.1.2. Алгоритм определения эффективных модули Юнга и коэффициентов Пуассона. Кинематико-статические и кинематические граничные условия.
1. Для определения эффективных модулей упругости 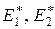 и эффективных коэффициентов Пуассона решим две задачи о поперечном растяжении ячейки периодичности, находящейся в плоском деформированном состоянии. Зададим кинематико-статические граничные условия, принимая во внимание симметрию ячейки периодичности, симметрию внешнего воздействия и используя установленные ранее свойства четности–нечетности компонентов вектора перемещения и тензора напряжений
и эффективных коэффициентов Пуассона решим две задачи о поперечном растяжении ячейки периодичности, находящейся в плоском деформированном состоянии. Зададим кинематико-статические граничные условия, принимая во внимание симметрию ячейки периодичности, симметрию внешнего воздействия и используя установленные ранее свойства четности–нечетности компонентов вектора перемещения и тензора напряжений
Задача (1):

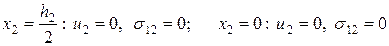 (3.1.4)
(3.1.4)
Задача (2):
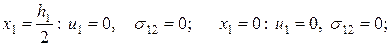
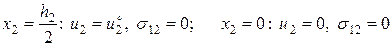 (3.1.5)
(3.1.5)
2. Вычислим средние тензоры микродеформаций 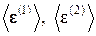 и средние тензоры микронапряжений
и средние тензоры микронапряжений 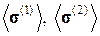 в задачах (1) и (2):
в задачах (1) и (2):
 (3.1.6)
(3.1.6)
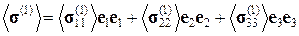
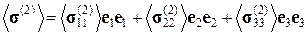 (3.1.7)
(3.1.7)
3. Используя эффективные определяющие соотношения (3.1.1) равенства (3.1.2) и выражения (3.1.6), (3.1.7), сформируем систему уравнений:
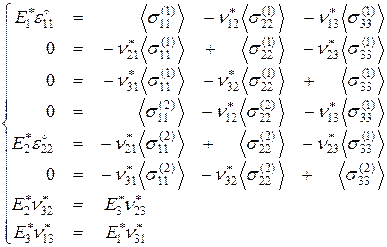 (3.1.8)
(3.1.8)
Система уравнений состоит из 8 уравнений с 8 неизвестными: 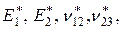
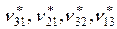 ; два последних уравнения являются нелинейными. Для компактного представления решения системы уравнений введем обозначения:
; два последних уравнения являются нелинейными. Для компактного представления решения системы уравнений введем обозначения:
|
|
|
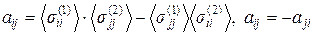 (3.1.9)
(3.1.9)
(по i, j – не суммировать). Тогда решение системы уравнений (3.1.8) имеет вид:
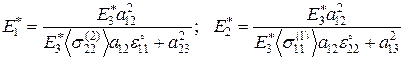 ;
;
 ; (3.1.10)
; (3.1.10)

4. Замечания.
4.1. В формулах (3.1.10) эффективный модуль Юнга 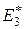 определяется выражением (3.1.3).
определяется выражением (3.1.3).
4.2. При формировании и решении системы уравнений (3.1.8) не использовалось равенство 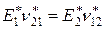 . Докажем, что эффективные модули Юнга
. Докажем, что эффективные модули Юнга 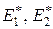 и коэффициенты Пуассона
и коэффициенты Пуассона 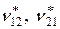 , определяемые соотношениями (3.1.10), удовлетворяют равенству
, определяемые соотношениями (3.1.10), удовлетворяют равенству 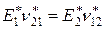 .
.
Используя выражение (3.1.10), получим:
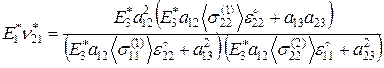 (3.1.11)
(3.1.11)
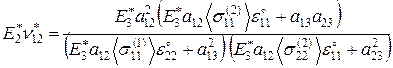 (3.1.12)
(3.1.12)
– равенство 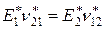 имеет место тогда и только тогда, когда:
имеет место тогда и только тогда, когда:
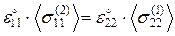 (3.1.13)
(3.1.13)
Преобразуем соотношение (3.1.13), используя выражения (3.1.6), (3.1.7):
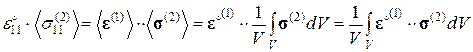
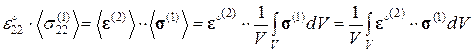
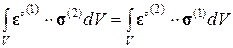 (3.1.14)
(3.1.14)
– одна из возможных форм записи теоремы взаимности Бетти. Следовательно, эффективные модули Юнга 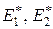 и коэффициенты Пуассона
и коэффициенты Пуассона 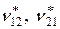 , определяемые соотношениями (3.1.10), удовлетворяют равенству:
, определяемые соотношениями (3.1.10), удовлетворяют равенству: 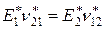 .
.
4.3. Для макроскопически трансверсально-изотропной гетерогенной среды формулы (3.1.10) дают правильный результат:
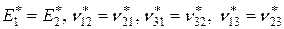 и число независимых эффективных упругих постоянных сокращается до 5.
и число независимых эффективных упругих постоянных сокращается до 5.
Пусть в задачах о поперечном растяжении ячейки периодичности, находящейся в условиях плоской деформации, заданы кинематические граничные условия Хашина – Розена:
Задача (1):

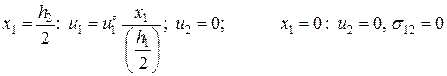 (3.1.15)
(3.1.15)
Задача (2):
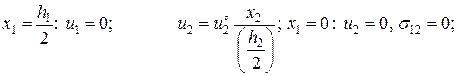
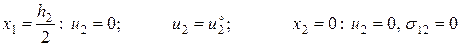 (3.1.16)
(3.1.16)
– граничные условия учитывают симметрию ячейки периодичности и симметрию внешнего воздействия. Решим указанные задачи.
|
|
|
Далее, для определения эффективных модулей Юнга и коэффициентов Пуассона в случае задания кинематических граничных условий, следует, выполнить пункты 2, 3, 4 вышеизложенного алгоритма.
3.1.3. Алгоритм определения эффективных модулей Юнга и коэффициентов Пуассона. Статические граничные условия.
1. В задачах о поперечном растяжении ячейки периодичности, находящейся в плоском деформированном состоянии, зададим статические граничные условия Хашина – Розена:
Задача (1):
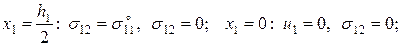 (3.1.17)
(3.1.17)
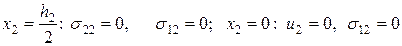
Задача (2):
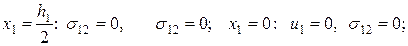 (3.1.18)
(3.1.18)
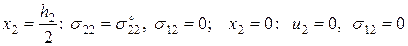
– граничные условия учитывают симметрию ячейки периодичности и симметрию внешнего воздействия. Решим указанные задачи.
2. Вычислим средние тензоры микродеформаций 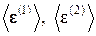 и средние тензоры микронапряжений
и средние тензоры микронапряжений 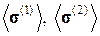 в задачах (1) и (2):
в задачах (1) и (2):
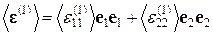
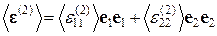 (3.1.19)
(3.1.19)
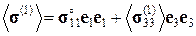
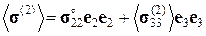 (3.1.20)
(3.1.20)
3. Используя эффективные определяющие соотношения (3.1.1), равенства (3.1.2) и выражения (3.1.19), (3.1.20), сформируем систему уравнений:
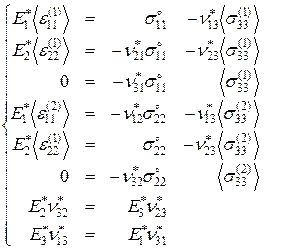 (3.1.21)
(3.1.21)
Система уравнений состоит из 8 уравнений с 8 неизвестными; два последних уравнения являются нелинейными. Решение системы уравнений (3.1.21) имеет вид:
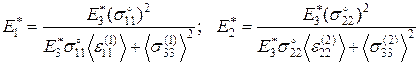 ;
;
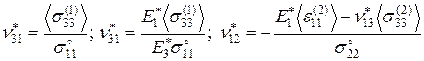 ; (3.1.22)
; (3.1.22)
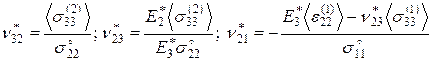
4. Замечания.
4.1. В формулах (3.1.22) эффективный модуль Юнга 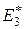 определяется выражением (3.1.3).
определяется выражением (3.1.3).
|
|
|
4.2. При формировании и решении системы уравнений (3.1.21) не использовалось равенство  . Докажем, что эффективные модули Юнга
. Докажем, что эффективные модули Юнга 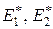 и коэффициенты Пуассона
и коэффициенты Пуассона 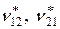 , определяемые соотношениями (3.1.22), удовлетворяют равенству
, определяемые соотношениями (3.1.22), удовлетворяют равенству 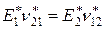 .
.
Используя выражение (3.1.22), получим:
 (3.1.23)
(3.1.23)
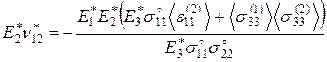 (3.1.24)
(3.1.24)
– равенство 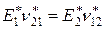 имеет место тогда и только тогда, когда:
имеет место тогда и только тогда, когда:
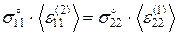 (3.1.25)
(3.1.25)
Преобразуем соотношение (3.1.25), используя выражения (3.1.19), (3.1.20):
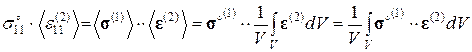
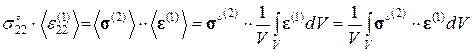
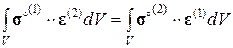 (3.1.26)
(3.1.26)
– из теоремы взаимности Бетти следует, что эффективные модули Юнга 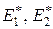 и коэффициенты Пуассона
и коэффициенты Пуассона 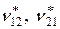 , определяемые соотношениями (3.1.22), удовлетворяют равенству:
, определяемые соотношениями (3.1.22), удовлетворяют равенству: 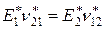 .
.
4.3. Для макроскопически трансверсально-изотропной гетерогенной среды формулы (3.1.22) дают правильный результат:
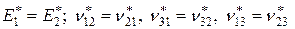
и число независимых эффективных упругих постоянных сокращается до 5.
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
