Нормальное распределение

⇐ ПредыдущаяСтр 8 из 24Следующая ⇒

Функция f(x) плотности вероятностей непрерывной СВ X, распределенной нормально с параметрами (m, s²), задается выражением (3.24):

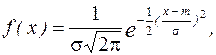(3.24)

где m - математическое ожидание СВ X;
s² - дисперсия СВ X.

4. Генерация псевдослучайных
числовых последовательностей

4.1. Моделирование псевдослучайной числовой
последовательности с равномерным законом распределения
алгоритмическим способом

Базовые понятия

Часто технические системы функционируют, находясь под влиянием непредсказуемых случайных факторов. Например, потоки запросов со стороны абонентов автоматической телефонной станции (звонки абонентов) к ресурсам телефонных каналов связи носят случайный характер. Подобные потоки можно прогнозировать только в статистическом смысле. Никогда нельзя предугадать абсолютно точно: сколько телефонных звонков со стороны абонентов поступит в течение какого-либо выбранного интервала времени и как долго будут заняты соответствующие телефонные каналы связи.

Разнообразные технические и человеко-технические системы, на поведение которых существенное влияние оказывают различные случайные факторы, называются системами массового обслуживания (СМО).

Понятно, что в процессе моделирования СМО необходимо моделировать различные случайные факторы, влияющие на их функционирование. Моделирование таких факторов базируется на генераторах последовательностей случайных числовых значений. Наиболее распространенным способом получения таких последовательностей является алгоритмический (программный) способ.

При алгоритмическом способе последовательность значений моделируемой случайной величины является по своей сути детерминированной, то есть предопределенной. Поэтому все алгоритмические способы порождают псевдослучайные последовательности значений величин. Приставка «псевдо» к слову «случайные» означает, что случайность фактически отсутствует, но получаемую при этом последовательность мы используем как случайную. Таким образом, термин «псевдослучайные» можно трактовать как «будто случайные».

В практике моделирования псевдослучайных числовых последовательностей функцию базовой выполняет последовательность с равномерным законом распределения на заданном интервале. Такая последовательность выполняет функцию базовой, потому что путем несложных функциональных преобразований она может быть преобразована в последовательность с любым другим заданным законом распределения.

4.1.2. Общий подход к получению
псевдослучайных последовательностей

Алгоритмы получения псевдослучайных последовательностей строятся на базе рекуррентных соотношений обычно первого порядка (4.1):

x_i₊₁ = R(x_i). (4.1)

В (4.1) R – это некоторая программно реализованная функция, для которой x_i является аргументом, а R(x_i) - значение функции.

Использование соотношения (4.1) предполагает, что первое число последовательности x₀ каким-либо способом задается. Поскольку R реализует некоторое функциональное преобразование, то для заданного значения аргумента x₀ функция R(x₀) вычислит вполне конкретное предопределенное алгоритмом значение x₁. При очередном обращении к R вычисленное только что значение x₁ будет подставлено в качестве аргумента. В результате функция R(x₁) вычислит вполне конкретное значение x₂, которое как понятно, было предопределено заданным значением x₀. Ясно, что и вся последующая цепочка значений x₃, x₄, … x_n предопределена первым заданным значением x₀. Поэтому в получаемой числовой последовательности случайность отсутствует, поэтому последовательность является псевдослучайной.

Для представления чисел последовательности используется вполне конкретная разрядная сетка (ЗС), имеющая фиксированную длину. Поэтому возможности любой такой РС по отображению все новых и новых значений ограничены. Например, на РС длиной 1 байт можно отобразить только 2⁸ = 256 разных чисел. Поэтому среди 257 чисел, записанных на такой РС, обязательно встретятся не менее 2-х одинаковых чисел. Применительно к рассматриваемой теме ограниченность длины РС приводит к тому, что в числовой последовательности, длина которой превышает некоторый порог, определяемый длиной РС, неизбежно появляется число, совпадающее с каким-либо предыдущим членом последовательности. Пусть, например, число x_m, совпало с числом x_p. Тогда очевидно, что R(x_m) = R(x_p), то есть x_m₊₁ = x_p₊₁. Тогда вся числовая последовательность, начинающаяся с числа x_m, неизбежно совпадет поэлементно с числовой последовательностью, начинающейся с числа x_p. В результате такого совпадения в генерируемой числовой последовательности появятся повторяющиеся цепочки чисел, которые назовем циклами. Таким образом, псевдослучайным последовательностям свойственно наличие циклов. При этом числа последовательности, не попавшие в цикл, появляются в ней ровно 1 раз. В результате, частота появления чисел, принадлежащих циклу, оказывается большей, чем частота появления чисел, не принадлежащих циклу. Такая предопределенная неравнозначность частот является нежелательной. Поэтому при разработке генераторов псевдослучайных последовательностей необходимо стремиться получать циклы по возможности наибольшей длины. В оптимальном случае длина цикла должна равняться количеству различных числовых кодов, отображаемых на данной РС.

Следует отметить, что для РС длиной, например, 8 байт количество различных отображаемых чисел равно 2⁶⁴и оно настолько велико, что ни одна программа никогда не потребует такого количества обращений к генератору псевдослучайных значений. Поэтому приведенные выше рассуждения о наличии циклов в генерируемых последовательностях актуальны при использовании сравнительно коротких разрядных сеток.

Метод Лемера

Генераторы псевдослучайных последовательностей отличаются конкретным содержанием функции R. Обычно в R реализуется функциональное преобразование, задаваемое линейной функцией. В методе Лемера [5], называемом также «линейный конгруэнтный метод», функция R задается выражением (4.2):

x_i+1 = (A x_i+B) mod C, (4.2)

где A, B, C – целые числа;
mod – операция вычисления остатка от деления.

Качество числовой последовательности, генерируемой в соответствии с (4.2), зависит от параметров A, B и C.

Возьмем, например, x₀ = A= B = 7, C=10. Получим следующую последовательность: 7, 6, 9, 0, 7, 6, 9, 0, 7, 6, 9, 0 и так далее. Как видно, полученная последовательность имеет очень короткий цикл, и использовать ее в качестве псевдослучайной неразумно. Причина плохого качества последовательности в плохом подборе параметров выражения (4.2).

Поскольку mod – операция вычисления остатка от деления, то x_i₊₁ < С. В результате цикл последовательности может иметь длину не более, чем C.

Существует теорема, доказанная М.Гринбергом для частного случая C=2^K.

Теорема. Длина периода линейной конгруэнтной последовательности равна C тогда и только тогда, когда:

1) B и M – взаимно простые числа;

2) D = A-1 кратно P для любого простого P, являющегося делителем числа C;

3) Если C кратно 4, то D кратно 4.

При использовании для представления чисел x_i, A и B РС длиной 2 байта можно рекомендовать следующие значения параметров:

A = 25173; B =13849; C =65536.

Метод Лемера при правильном подборе параметров порождает целочисленные числовые последовательности, закон распределения которых достаточно хорошо приближен к равномерному распределению на интервале [ 0, C-1 ].

В языке Pascal имеется встроенный генератор псевдослучайных последовательностей Random:

0 £ Random < 1 (4.3)

Для того чтобы генератору, реализующему метод Лемера и работающему на множестве целых чисел, придать свойства стандартного генератора Random достаточно при обращении к соответствующей подпрограмме функции возвращать 2 значения:

- первое – целое число x_i₊₁, вычисленное непосредственно по выражению (4.2);

- второе - значение равное x_i₊₁ / C.

Понятно, что поскольку x_i₊₁ Î [ 0, C-1 ], то x_i₊₁ / C Î [ 0, 1).

5. Основы теории
систем массового обслуживания

Дата добавления: 2016-01-04; просмотров: 16; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!