Сравнение двух дисперсий нормальных

Проверка статистических гипотез

Статистической гипотезой Н называется предположение относительно параметров или вида распределения случайной величины Х. Если распределение случайной величины Х известно и по выборке наблюдений необходимо проверить предположение о значении параметров этого распределения, то такие гипотезы называются параметрическими.

Проверяемая гипотеза называется нулевой гипотезой Н₀. Вместе с гипотезой Н₀ рассматривают одну из альтернативных (конкурирующих) гипотез Н₁. Правило, по которому принимается решение принять или отклонить гипотезу Н₀, называется критерием. Статистика Z, на основании которой принимается решение об истинности гипотезы Н₀, называют статистикой критерия. При проверке параметрической гипотезы Н₀: q = q₀ в качестве статистики критерия обычно выбирают ту же статистику, что и для оценки параметра q.

Перед анализом выборки назначается некоторая малая вероятность α, называемая уровнем значимости. Пусть V – множество значений статистики Z, а V_k – такое подмножество, что при условии истинности гипотезы Н₀, вероятность попадания статистики критерия в V_k равна α:

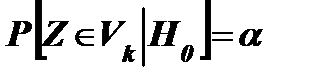Пусть z_в – выборочноезначение статистики Z, вычисленное по выборке. Формулировка критерия: отклонить гипотезу Н₀, если 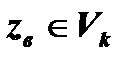(попадание в критическую область); принять гипотезу Н₀, если 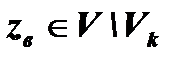( попадание в область принятия гипотезы).

Уровень значимости α определяет размер критической области V_k. Положение критической области на множестве значений статистики Z зависит от формулировки альтернативной гипотезы Н₁. 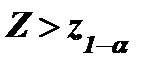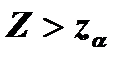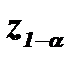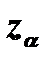Если проверяется гипотеза Н₀: q = q₀, а альтернативная гипотеза Н₁: q > q₀ (q < q₀), то критическая область размещается на правом (левом) хвосте плотности распределения статистики Z, то есть имеет вид неравенства: ( ), где и - квантили распределения статистики Z порядка 1-α и α, вычисленные при условии истинности Н₀. В этом случае критерий называется односторонним, соответственно право- и левосторонним. Если альтернативная гипотеза Н₁: q ≠ q₀, критическая область размещается на обоих хвостах плотности распределения Z, то есть определяется неравенствам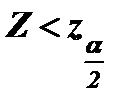и: и 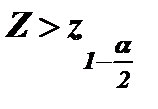. В этом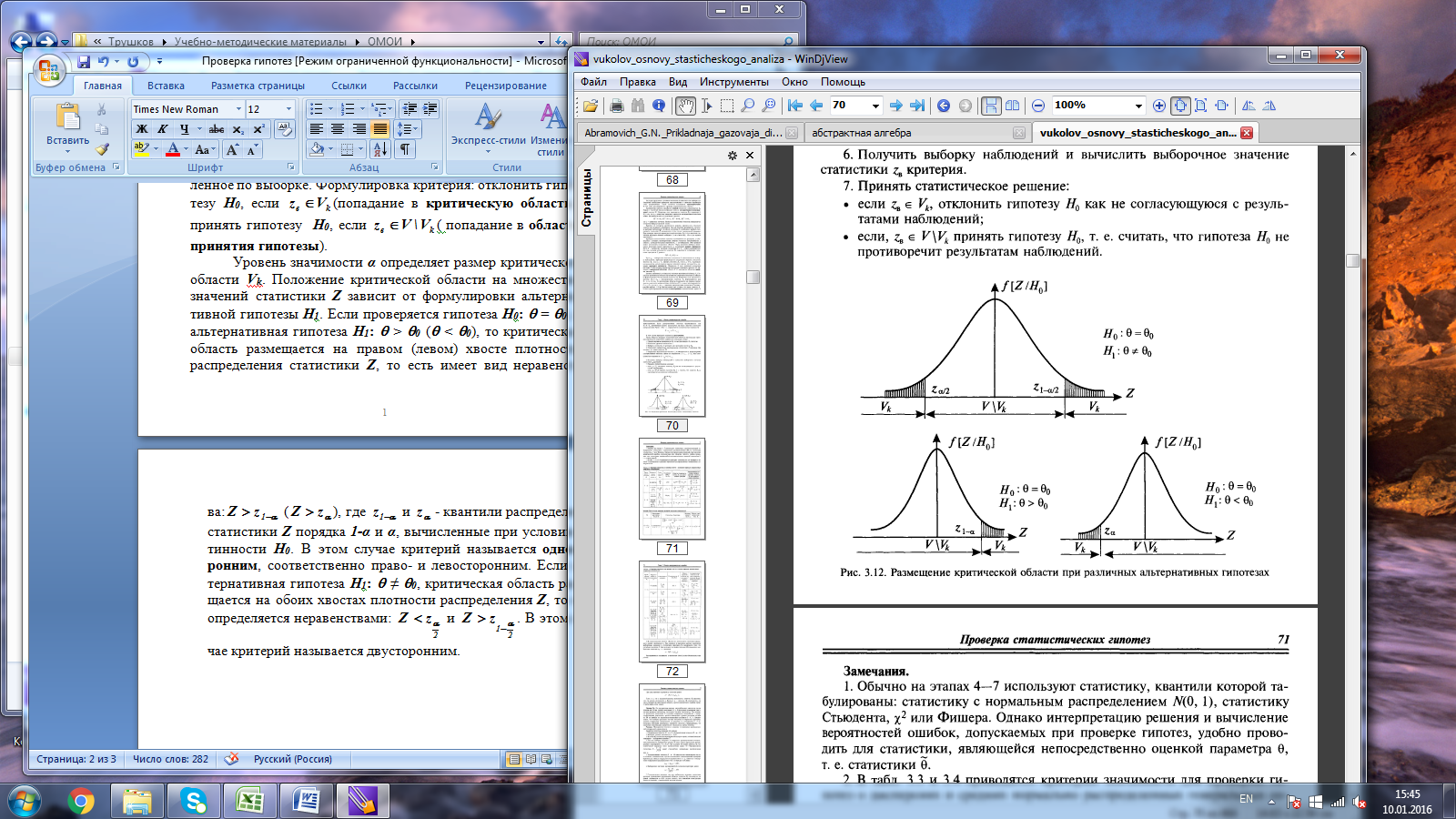

Размещение критической области при различных альтернативных гипотезах

случае критерий называется двусторонним.

Таким образом, проверка статистической гипотезы при помощи критерия значимости состоит в следующем:

1. Сформулировать гипотезы Н₀ и Н₁.

2. Назначить уровень значимости α.

3. Выбрать статистику Z критерия для проверки Н₀.

4. Определить выборочное распределение статистики Z критерия при условии, что верна Н₀.

5. Определить критическую область V_k.

6. По выборке вычислить выборочное значение статистики z_в критерия.

7. Принять статистическое решение: если 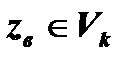, отклонить Н₀; если 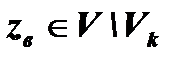, принять Н₀, то есть Н₀ не противоречит результатам наблюдений.

Сравнение двух дисперсий нормальных

Генеральных совокупностей

1. При заданном уровне значимости α по двум выборкам объемов n₁ и n₁проверить нулевую гипотезу H₀ : D( X) = D( Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H₁ : D( X) > D( Y). В качестве критерия выбирается отношение большей дисперсии к меньшей 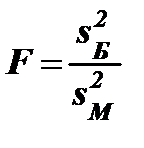~F( n₁- 1, n₂ - 1), имеющей распределение Фишера с n₁ - 1 и n₂ - 1 степенями свободы (n₁ – объем выборки с большей дисперсией).

Надо вычислить выборочное (наблюдаемое) значение критерия (отношение большей дисперсии к меньшей) 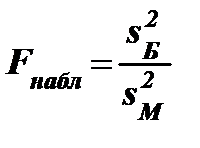. Критическая область – односторонняя и определяется по правилу: 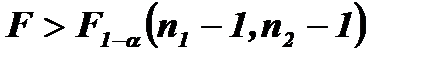, где 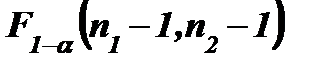- квантиль распределения Фишера с n₁ - 1 и n₂ - 1 степенями свободы порядка 1-α. Введем критическое число 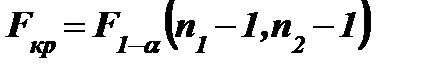, отделяющее критическую область от области принятия гипотезы. По заданному уровню значимости α и числамстепеней свободы n₁ - 1 и
n₂- 1 (n₁ – объем выборки с большей дисперсией) найти критическую точку с помощью встроенной функции

F_кр = FРАСПОБР(Вероятность, Степени_свободы1, Степени_свободы2).

Параметры Вероятность = α, Степени_свободы1 = n₁- 1, Степени_свободы2 = n₂ – 1.

Если F_набл < F_кр – нет оснований отвергнуть нулевую гипотезу.

Если F_набл > F_кр – нулевая гипотеза отвергается.

2. Пусть при проверке той же нулевой гипотезы
H₀ : D( X)= D( Y) используется конкурирующая гипотеза
H₁ : D( X) ≠ D( Y). Используем тот же статистический критерий ~F( n₁- 1, n₂ - 1). Критическая область - двусторонняя, но так как при формировании критерия F > 1 по определению, то она определяется по правилу 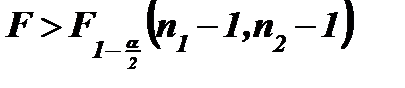. Критическое число 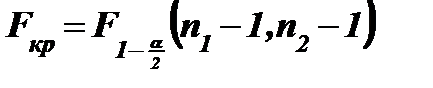определяется с помощью встроенной функции

F_кр = FРАСПОБР(Вероятность, Степени_свободы1, Степени_свободы2).

Параметры Вероятность= α/2, Степени_свободы1= n₁- 1, Степени_свободы2= n₂ – 1.

Если F_набл < F_кр – нет оснований отвергнуть нулевую гипотезу.

Если F_набл > F_кр – нулевая гипотеза отвергается.

Дата добавления: 2018-10-27; просмотров: 290; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!