Сравнение выборочной дисперсии с гипотетической

Генеральной дисперсией нормальной совокупности

1. При заданном уровне значимости α по выборке объемом n проверить нулевую гипотезу H₀ : D( X) = о равенстве генеральной дисперсии D( X) гипотетическому значению при конкурирующей гипотезе H₁ : D( X) > . В качестве критерия выбирается статистика ~ , имеющая распределение c² с n -1 степенью свободы.

Наблюдаемое значение критерия вычисляется по выборке . Критическая область - правосторонняя и определяется по правилу , где - квантиль распределения c² с n -1 степенью свободы порядка 1- α. Введем критическое число , которое вычислим с помощью встроенной функции:

=ХИ2ОБР(Вероятность, Степени_свободы).

Параметры Вероятность = α, Степени_свободы = n-1.

Если < – нет оснований отвергнуть нулевую гипотезу.

Если > – нулевая гипотеза отвергается.

2. Пусть проверяется та же нулевая гипотеза H₀: D( X) = при альтернативе H₁ : D( X) < . Используем тот же статистический критерий . Критическая область - левосторонняя и определяется по правилу . Критическое число вычислим с помощью встроенной функции:

=ХИ2ОБР(Вероятность, Степени_свободы).

Параметры Вероятность = 1-α, Степени_свободы = n-1.

Если > – нет оснований отвергнуть нулевую гипотезу.

Если < – нулевая гипотеза отвергается.

3. Пусть при проверке нулевой гипотезы H₀: D( X) = используется альтернатива H₁ : D( X) ≠ . Критическая область – двусторонняя и определяется условиями или . Таким образом, область принятия гипотезы определяется соотношением: 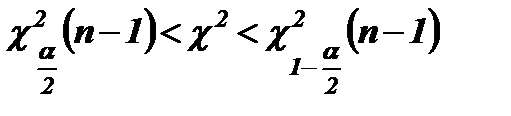. Введем левую и правую критические точки, которые вычисляем с помощью встроенной функции:

ХИ2ОБР(Вероятность, Степени_свободы).

Параметр Степени_свободы = n – 1 для обеих критических точек, а параметр Вероятность = 1 – α/2 при вычислении левой критической точки и параметр Вероятность = α/2 при вычислении правой критической точки.

Если < < 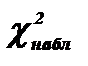– нет оснований отвергнуть нулевую гипотезу.

В противном случае нулевая гипотеза отвергается.

Сравнение двух средних генеральных

Совокупностей, дисперсии которых известны

1. При заданном уровне значимости α по двум выборкам объемами n и m проверить нулевую гипотезу H₀: M( X)= M( Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе H₁: M( X) ≠ M( Y). В качестве критерия выбирается статистика ~ N(0,1), имеющая стандартное (нормированное) нормальное распределение.

Наблюдаемое значение критерия вычисляется по выборкам . Критическая область - двусторонняя и определяется условиями или , где u_α - квантиль нормального нормированного распределения порядка α. Таким образом, область принятия гипотезы определяется соотношением: . Учитывая, что для нормального нормированного распределения имеет место , область принятия гипотезы определяется неравенством . Введем критическое число , которое вычислим с помощью встроенной функции:

z_кр = НОРМСТОБР(Вероятность).

Параметр Вероятность = 1 – α/2.

Если – нет оснований отвергнуть нулевую гипотезу.

Если – нулевая гипотеза отвергается.

2. Пусть при проверке нулевой гипотезы H₀: M( X) = M( Y) используется альтернатива H₁: M( X) > M( Y). Используем тот же статистический критерий . Критическая область - правосторонняя и определяется по правилу . Критическое число вычислим с помощью встроенной функции:

z_кр = НОРМСТОБР(Вероятность).

Параметр Вероятность = 1 – α.

Если – нет оснований отвергнуть нулевую гипотезу.

Если – нулевая гипотеза отвергается.

3. Пусть при проверке нулевой гипотезы H₀: M( X) = M( Y) используется альтернатива H₁: M( X) < M( Y). Используем тот же статистический критерий . Критическая область - левосторонняя и определяется по правилу . Критическое число вычислим с помощью встроенной функции:

z_кр = НОРМСТОБР(Вероятность).

Параметр Вероятность = α.

Если 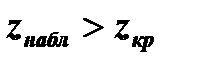– нет оснований отвергнуть нулевую гипотезу.

Если – нулевая гипотеза отвергается.

Дата добавления: 2018-10-27; просмотров: 357; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!