Общие принципы выполнения проектных и поверочных расчетов
Элементов конструкций
Расчеты на прочность
Прочность – способность конструкции, ее узлов и деталей выдерживать определенную нагрузку, не разрушаясь.
Существует два основных метода расчета элементов конструкций на прочность:
1. расчет по предельным напряжениям;
2. расчет по разрушающим нагрузкам.
Метод расчета по напряжениям наиболее распространен. Согласно этому методу необходимо определить значения напряжений в наиболее опасных сечениях элемента и сопоставить их с предельными значениями для данного материала. В качестве предельных напряжений могут быть выбраны пределы текучести или прочности, однако наиболее часто используют допускаемые напряжения, полученные делением соответствующих пределов на коэффициенты запаса:
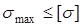 .
.
Из результатов сопоставления делают вывод о прочности конструкции.
Метод расчета по разрушающим нагрузкам используют в основном для деталей из пластичных материалов (малоуглеродистых сталей, меди, алюминия, бронзы). Согласно этому методу необходимо определить предельную нагрузку, которую может выдержать элемент, не разрушаясь и не изменяя свою форму. После сопоставления рабочей нагрузки с предельной, делают вывод о прочности конструкции. Недостатком этого метода является сложность определения предельной нагрузки для сложных конструкций.
Элементы конструкций, подверженные действию внешних нагрузок имеют следующий характер деформации: растяжение, сжатие, изгиб, кручение, срез.
|
|
|
Растяжение - сжатие
При растяжении (сжатии) элемента конструкции силой N в любом поперечном сечении площадью A, все точки поперечного сечения деформируются одинаково, а значит, нормальные напряжения будут одинаковы по всему сечению
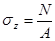 .
.
Из закона Гука 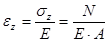 ,
,
Где Е × А – жесткость стержня при растяжении-сжатии.

Кручение
При кручении элемента круглого поперечного сечения, происходит поворот сечений вокруг оси z , при этом формула касательных напряжений имеет простой вид
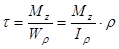 ,
,
где М z – крутящий момент относительно оси z; W r - полярный момент сопротивления, м3; I r - полярный момент инерции сечений, м4;
Эпюра касательных напряжений имеет форму треугольника.
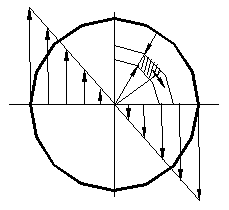
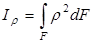
Определение касательных напряжений в стержне с некруглым поперечным сечением представляет собой более сложную задачу. Это связано с тем, что поперечные сечения заметно искривляются (депланация сечения).
Рассмотрим кручение тонкостенной трубы некруглой формы. В этой связи введем допущение, что касательные напряжения t распределены равномерно по толщине стенки s.
Направление t в каждой точке контура совпадает с касательной к контуру.
|
|
|
Введем понятие потока касательных сил (Н/м), представляющего собой силу, приходящуюся на единицу длины контура сечения:
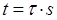 , или
, или 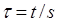

Найдем поток t , предполагая, что этот поток вызван известным действующим крутящим моментом М z.
 ,
,
где d W = dl × r – удвоенная площадь сектора в виде элементарного треугольника с основанием dl; W - удвоенная площадь, охватываемая контуром сечения.
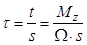 .
.
Изгиб
Рассмотрим наиболее простой случай изгиба – чистый изгиб, имеющий место только в одной плоскости. Волокна стержня, нагруженного моментом М x , с выпуклой стороны растягиваются, а с вогнутой - сжимаются. На середине сечения (ось стержня) находятся нейтральные волокна. При чистом изгибе ось однородного стержня не изменяет своей длины, принимая форму дуги окружности.

Считают, что нормальные напряжения в направлении оси z намного больше напряжений, развивающихся в направлении осей x и y, поэтому последними пренебрегают:
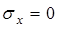 ;
; 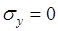 ;
; 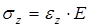 ; (1)
; (1)
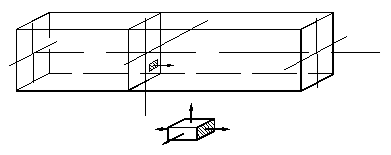
Принятые допущения:
1) продольные волокна стержня не оказывают давления друг на друга;
2) поперечные сечения стержня после деформации остаются плоскими и перпендикулярными к оси стержня.
|
|
|
Рассмотрим два сечения, отстоящих друг от друга на расстоянии dz. В результате изгиба одно сечение поворачивается относительно другого на угол d q.

Относительное удлинение внешних волокон (АВ)
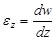 , (2)
, (2)
где dw – приращение длины АВ,
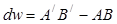 ,
,
до изгиба АВ=С D = dz ,
из треугольника: 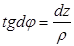 Þ
Þ  Þ
Þ 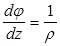 . (3)
. (3)
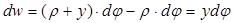
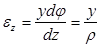 , тогда (4)
, тогда (4)
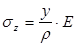 , (5)
, (5)
т.е. напряжения по высоте сечения изменяются по линейному закону и принимают максимальные значения в крайних точках сечения.
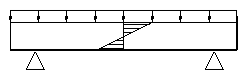 |
В общем случае, в поперечных сечениях стержня могут действовать: нормальная сила N; изгибающий момент My; изгибающий момент Mx, которые могут быть выражены через напряжения 
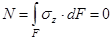 Þ
Þ  Þ, т.е. (6)
Þ, т.е. (6)
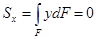 - статический момент сечения (если Sx = 0, то ось x проходит через центр тяжести сечения)
- статический момент сечения (если Sx = 0, то ось x проходит через центр тяжести сечения)
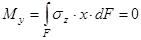 Þ
Þ 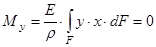 Þ, т.е. (7)
Þ, т.е. (7)
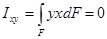 - центробежный момент инерции сечения (если Ixy = 0, то оси x и y являются главными)
- центробежный момент инерции сечения (если Ixy = 0, то оси x и y являются главными)
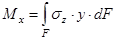 Þ
Þ  Þ
Þ 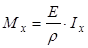 (8)
(8)
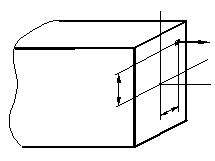
Из формул (5) и (8) получим выражение для определения напряжения:
|
|
|
 (9)
(9)
Наибольшие напряжения определяют по формуле
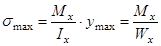 ,
,
где 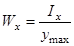 - момент сопротивления сечения при изгибе, м3.
- момент сопротивления сечения при изгибе, м3.
Ix – осевой момент инерции поперечного сечения, м4.
 |
Для прокатных профилей (двутавр, швеллер, уголок и др.) значения геометрических характеристик Ix , Wx приводятся в таблицах сортамента.
Из формул (3) и (8) получаем зависимость между изгибающим моментом и кривизной элемента стержня
 , (10)
, (10)
знак «-» говорит о том, что перемещение точки К сечения при изгибе происходит в сторону, противоположную направлению нормальных напряжений s z .
Произведения EIx , EIy называют жесткостью сечения при изгибе относительно соответствующей оси.
В общем случае изгиба
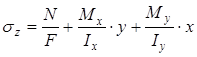 (11)
(11)
Расчеты на жесткость
Жесткость – способность конструкции, ее узлов и деталей выдерживать определенную нагрузку без существенного изменения геометрических размеров.
Чтобы сделать вывод о жесткости конструкции, необходимо определить возможные перемещения ее элементов.
Перемещения при растяжении (сжатии)
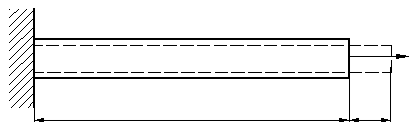
Линейная деформация стержня, нагруженного осевой силой ( 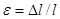 ):
):
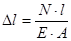 , (12)
, (12)
Из формулы (12) видно, что деформация стержня возрастает при увеличении его длины и нагружающей его силы, а также с уменьшением площади поперечного сечения.
Перемещения при кручении
При кручении касательные напряжения связаны с угловой деформацией соотношением – законом Гука для сдвига
 , (13)
, (13)
где 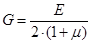 - модуль сдвига (модуль упругости 2-го рода), Па.
- модуль сдвига (модуль упругости 2-го рода), Па.
В результате приложения крутящего момента М z поперечные сечения стержня получают взаимные угловые смещения j, а продольные сечения – угловую деформацию g, они связаны между собой:
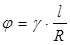 (14)
(14)
Используя формулу  и соотношения (13) и (14), получим (r = R)
и соотношения (13) и (14), получим (r = R)
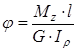 , (15)
, (15)
G × I r - жесткость стержня при кручении.
Перемещения при изгибе
Прогиб y – это перемещение центра тяжести сечения в направлении главной оси сечения.
Положение центров тяжести поперечных сечений стержня в деформированном состоянии определяется функцией прогибов y=y(z).
Кроме прогиба поперечное сечение поворачивается относительно оси y на угол j. Этот угол равен углу между касательной к линии прогибов и осью стержня z (согласно принятому допущению).

Кривая прогибов описывается некоторой функцией y=y(z), а тангенс угла наклона касательной к кривой равен первой производной от этой функции
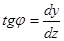 , (12)
, (12)
т.к. величина угла поворота j небольшая, то
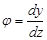 . (13)
. (13)
Уравнения (10) и (13) образуют систему
 Þ
Þ 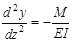 (14)
(14)
Учитывая, что поперечная сила 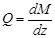 и распределенная нагрузка
и распределенная нагрузка 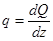 , система уравнений (14) может быть дополнена еще двумя:
, система уравнений (14) может быть дополнена еще двумя:
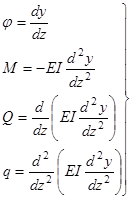 , (15)
, (15)
в случае стержня постоянного поперечного сечения EI=const и последние два уравнения можно записать следующим образом
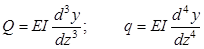 .
.
Таким образом, если известна схема нагружения стержня, можно путем последовательного интегрирования уравнений (15), сформулировав граничные условия, можно получить функцию прогибов стержня.
Например
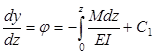
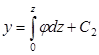 , (16)
, (16)
где постоянные интегрирования С1 = j0 и С2 = y0 выражают угол поворота и прогиб в начале координат (z=0).
Методы решения дифференциального уравнения прогибов
1. Метод начальных параметров
Решение по этому методу представляется в виде формулы общего вида для определенного n-го участка стержня.
Для этого рассматриваемый стержень разбивают на n участков, на каждом из которых может быть определена функция прогибов.
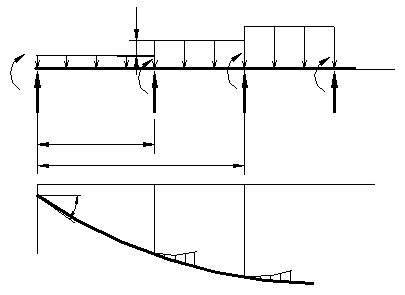
На первом участке стержня функцию прогибов раскладывают в ряд Макларена:
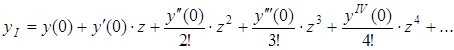 , (17)
, (17)
т.к. 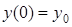 ;
; 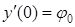 ;
; 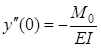 ;
; 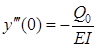 ;
; 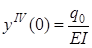
то
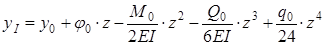 . (18)
. (18)
Прогибы на втором участке
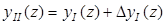 , (19)
, (19)
где D yI – разность между истиной линией прогибов на 2-м участке и продолжением функции yI в пределах 2-го участка.
Аналогично функции yI , функцию D yI также можно разложить в ряд, при этом текущая координата отсчитывается от начала 2-го участка:
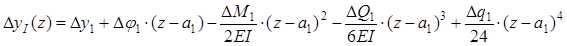 ,(20)
,(20)
где D М1 , D Q 1 – сосредоточенные изгибающий момент и поперечная сила на переходе от 1-го к 2-му участку;
D q 1 – разность в величине распределенной нагрузке на границе участков;
D y 1 , D j 1 – скачки прогиба и угла поворота на границе участков (т.к. линия прогибов обычно непрерывна D yi=0, D j i=0)
Таким образом, для произвольного n-го участка:
 (21)
(21)
Формула для углов поворота получается дифференцированием 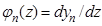
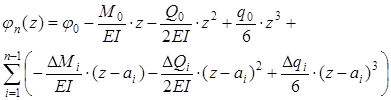 (22)
(22)
Величины y 0, j 0, M 0, Q 0 – находятся из граничных условий.
Расчеты на устойчивость
Устойчивость – способность конструкции, ее узлов и деталей сохранять свое состояние (форму) при внешних воздействиях.
Потеря устойчивости – переход системы от исходного положения равновесия в новое состояние.
Примеры потери устойчивости: центрально-сжатый стержень; тонкостенная труба, нагруженная внешним давлением, осевой сжимающей силой, крутящим моментом.
Потеря устойчивости может произойти:
- при напряжениях значительно меньше допускаемых по прочности (после снятия нагрузки элемент конструкции восстанавливает свою первоначальную форму);
- при напряжениях, превышающих предел текучести (после снятия нагрузки в конструкции сохраняются остаточные деформации).
Во многих случаях система, потерявшая устойчивость, переходит в новое состояние равновесия, сохраняя работоспособность и способность выполнять свои функции (например, тонкостенные оболочки).
В некоторых случаях, не обладая устойчивыми положениями равновесия, система может перейти в режим незатухающих колебаний.
Вывод формулы Эйлера для критической силы
Рассмотрим задачу о равновесии прямолинейного стержня, сжатого осевой силой F. Предположим, что под действием этой силы стержень получил искривление оси. Стержень будет находиться в равновесии, если момент, вызванный действием силы F , будет уравновешен изгибающим моментом M, действующим в поперечном сечении стержня:
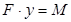 (23)
(23)
При малых прогибах можно записать равенство (14)
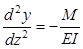 Þ
Þ 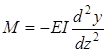
Тогда уравнение равновесия запишется в виде:
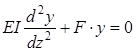 (24)
(24)
Обозначив 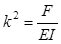 , запишем уравнение (24)
, запишем уравнение (24)
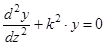 (25)
(25)
Решение однородного дифференциального уравнения (25) можно представить в виде:
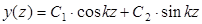 . (26)
. (26)
Постоянные C1 и С2 находят из граничных условий:
При z=0 y=0; Þ С1=0 Þ 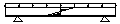
При z=l y=0 Þ 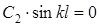 .
.
Если С2=0, тогда прогибы = 0 и стержень имеет прямолинейную форму равновесия.
Если 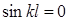 , то
, то 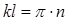 , где n = 1, 2, 3, …(число волн)
, где n = 1, 2, 3, …(число волн)
В результате
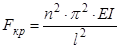 . (27)
. (27)
Наименьшая критическая сила будет при n=1
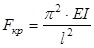 - формула Эйлера (28)
- формула Эйлера (28)
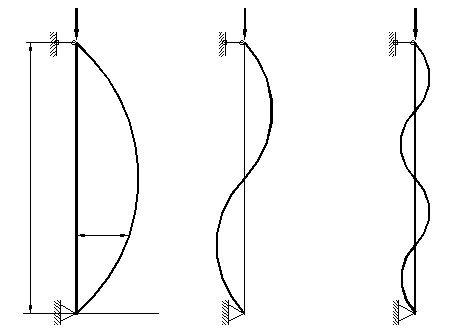
Способ закрепления стержня влияет на величину критической силы, для этого в формулу Эйлера (28) вводится коэффициент приведения длины m.
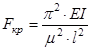 (29)
(29)
Значение коэффициента определяют исходя из геометрической аналогии путем сопоставления упругой линии изогнутого стержня с длиной полуволны синусоиды при шарнирном закреплении.
Для очень коротких стержней при воздействии на них осевой сжимающей силой, напряжения в материале могут превышать предел прочности. В этом случае не будет соблюдаться закон Гука и расчет по формуле Эйлера окажется неприемлемым.
Напряжения, соответствующие критической силе:
 , (30)
, (30)
где 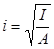 - радиус инерции поперечного сечения стержня.
- радиус инерции поперечного сечения стержня.
Величина 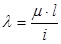 называется гибкостью стержня.
называется гибкостью стержня.
Тогда
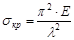 . (31)
. (31)
Из выражения (31), заменяя напряжение на предел прочности sВ найдем предельную величину гибкости
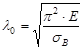 (32)
(32)
При l>l0 для определения критической силы можно пользоваться формулой Эйлера.
Для проверки стержней на устойчивость должно быть выполнено условие
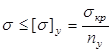 , (33)
, (33)
где n у – коэффициент запаса устойчивости.
При расчете на прочность полагается
Отношение допускаемых напряжений 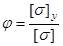 называется коэффициентом продольного изгиба и определяет степень снижения расчетного сопротивления материала при продольном изгибе.
называется коэффициентом продольного изгиба и определяет степень снижения расчетного сопротивления материала при продольном изгибе.
Расчеты на усталостную прочность
Усталость материала – процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к разрушению.
Выносливость – способность материала противостоять усталости.
В расчетах на прочность обычно делалось допущение об однородности структуры материала. На самом деле структурная неоднородность материала при воздействии переменных напряжений, даже не превосходящих предела текучести приводит к образованию пластических деформаций (из-за деформаций сдвига) в неблагоприятно ориентированных зернах кристаллической решетки. Следствием этого является образование микротрещин в материале, которые затем развиваются в макротрещины и со временем происходит разрушение материала.
В настоящее время теория усталостной прочности материалов и методики расчета на выносливость основаны на экспериментальных данных.
Рассмотрим вал, вращающийся с постоянной угловой скоростью w [рад/с]. Тогда напряжения в произвольной точке А, расположенной на диаметре вала будут изменяться в соответствии с законом:
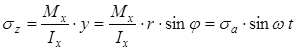 , (34)
, (34)
где 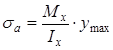 - амплитудное (максимальное) значение напряжения.
- амплитудное (максимальное) значение напряжения.
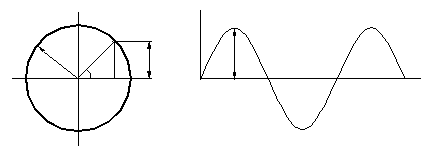
Соответственно уравнению (34) график изменения напряжения будет представлять собой синусоиду. Такой цикл изменения напряжений называется симметричным.
Если вдоль оси вала будет действовать растягивающая или сжимающая нормальная сила N, то в этом случае цикл изменения нормальных напряжений будет асимметричным
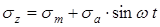 , (35)
, (35)
где 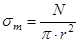 .
.

Циклические напряжения характеризуются следующими параметрами:
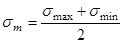 - среднее напряжение цикла
- среднее напряжение цикла
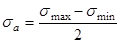 - амплитуда цикла
- амплитуда цикла
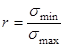 - коэффициент асимметрии цикла (для пульсационного цикла r=0, для симметричного цикла r = -1).
- коэффициент асимметрии цикла (для пульсационного цикла r=0, для симметричного цикла r = -1).
Для асимметричных циклов экспериментально получают диаграмму предельных амплитуд, т.е. зависимость между амплитудами циклов s а и средними напряжениями циклов s m .

Назначение диаграммы предельных амплитуд состоит в том, что если рабочая точка, соответствующая значениям s а и s m лежит ниже кривой s а=f(s m), то образец не разрушится до базового числа циклов, если выше – то образец разрушится при числе циклов меньше базового.
Что не проводить трудоемкие эксперименты для получения диаграммы предельных амплитуд, ее схематизируют по 4-м точкам. Верхняя часть кривой заменяется прямой, проходящей через точки А (соответствует симметричному циклу s m=0) и В (соответствует пульсационному циклу s а=s m=s о/2).
Прямая АВ описывается уравнением
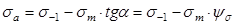 , (36)
, (36)
где 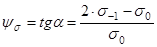 .
.
Прямая С D описывается уравнением
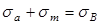 , (37)
, (37)
т.е. максимальное напряжение не должно превосходить предела прочности материала. Для пластичных материалов в правой части уравнения (37) выбирается предел текучести s Т.
Диаграмма предельных амплитуд строится на основании испытаний специальных образцов, а, следовательно, формула (36) справедлива также для образца материала. Переходя к конкретной детали, следует учитывать такие факторы, снижающие усталостную прочность материала, как
- концентрация напряжений;
- размеры детали;
- качество обработки поверхности детали.
Это приводит к тому, что амплитуда циклов s а для конкретной детали уменьшится в К раз. В результате линия АВ на диаграмме предельных амплитуд опустится ниже.
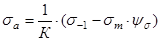 , (38)
, (38)
где 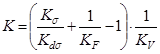 - коэффициент уменьшения предела выносливости.
- коэффициент уменьшения предела выносливости.
К s - эффективный коэффициент концентрации напряжений, представляющий собой (для симметричных циклов) отношение пределов выносливости гладкого образца s-1 и образца, имеющего концентрацию напряжений s /-1:
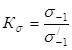 .
.
Значения коэффициента К s приведены в таблицах и графиках, полученных экспериментально. Можно также пользоваться формулой:
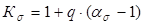 , (39)
, (39)
где  - теоретический коэффициент концентрации напряжений, представляющий собой отношение наибольших местных напряжений вблизи концентратора напряжений к номинальным напряжениям при условии отсутствия концентраторов напряжений. Значения a s приведены в справочниках.
- теоретический коэффициент концентрации напряжений, представляющий собой отношение наибольших местных напряжений вблизи концентратора напряжений к номинальным напряжениям при условии отсутствия концентраторов напряжений. Значения a s приведены в справочниках.
q – коэффициент чувствительности материала к местным напряжениям, зависящий от свойств материала
- для высоколегированных сталей q»1
- для конструкционных сталей q=0,6-0,8
- для низколегированных сталей q=0,4-0,6
- для углеродистых сталей и алюминиевых сплавов q=0,3-0,5
- для серого чугуна q=0,1-0,2.
К d s (<1) - коэффициент масштабного фактора, учитывающий уменьшение сопротивления усталости с увеличением размеров детали по сравнению со стандартным образцом диаметром 7,5 мм.
К F – коэффициент качества поверхности, учитывающий уменьшение усталостной прочности с увеличением высоты микронеровностей поверхности по сравнению со шлифованной.
- шлифование К F =1;
- токарная обработка сталей К F =1,05-1,25;
- токарная обработка алюминия К F =0,8-0,9;
- необработанные поверхности К F =1,35-2,2.
К V – коэффициент, учитывающий влияние поверхностного упрочнения
- закалка ТВЧ К V = 1,3-1,6 - без концентрации напряжений (1,6-2,8) - с концентрацией напряжений;
- азотирование К V =1,15-1,25 (1,9-3,0);
- цементация К V=1,2-2,1 (1,5-2,5)
- обкатка роликами К V =1,1-1,25 (1,3-1,8)
- обдув дробью К V =1,1-1,3 (1,4-2,5).
Близость рабочих условий к предельным (линии АВ) характеризуется коэффициентом запаса циклической прочности n -1
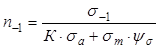 (40)
(40)
Данные по пределам выносливости для симметричных циклов приводятся в справочниках.
Для сталей предел выносливости можно оценивать по эмпирической формуле
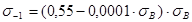 .
.
Для цветных металлов
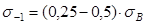 .
.
Расчеты на ударную прочность
Ударная прочность – способность конструкции, ее узлов и деталей выдерживать динамическую нагрузку, не разрушаясь.
Динамическая нагрузка – в результате приложения которой, возникает состояние неравномерного (с ускорением) движения системы.
Согласно принципу Даламбера, на движущуюся систему тел действуют силы инерции, направленные противоположно ускорению 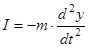 .
.
Расчет конструкций с учетом сил инерции и возникающего движения масс системы называют динамическим расчетом.
Одним из видов динамического расчета является расчет на ударную прочность.
Взаимодействие тел, при котором за очень малый промежуток времени скачкообразно возникают конечные изменения скорости этих тел, называют ударом.
Механизм удара
Рассмотрим взаимодействие вертикально падающего груза массой m 1 и упругой конструкцией, имеющей массу m 2.
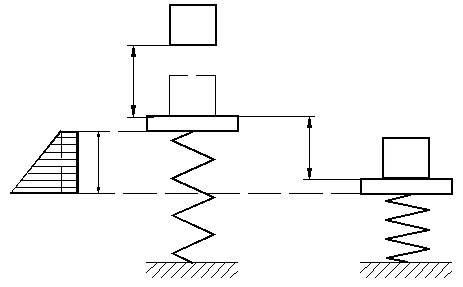

В момент контакта двух тел, между ними возникает сила взаимодействия, зависящая от времени контакта N=N(t).
Период контакта двух соударяющихся тел t=t1+t2,
где t1 – фаза сближения центров тел за счет местных контактных деформаций; t2 – фаза упругого отталкивания тел.
Площадь диаграммы N(t) соответствует импульсу, сообщаемому ударяемому телу 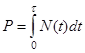 . Этот импульс вызывает у ударяемого тела массой m возникновение конечной скорости движения в направлении удара.
. Этот импульс вызывает у ударяемого тела массой m возникновение конечной скорости движения в направлении удара.
Математическая модель удара
Принятые допущения:
1 – в конструкции при ударе не возникают волны упругих деформаций;
2 – удар двух тел является абсолютно неупругим (без отскока);
Введем обозначения:
m 1 – масса ударяющего тела, падающего с высоты h;
m 2 – масса ударяемого тела, закрепленного на пружине;
G1=m1×g – вес падающего тела;
V – скорость падающей массы m 1;
V0 – начальная скорость движения системы тел (m 1+m 2) после соударения;
h – начальная высота поднятой массы;
y – перемещение системы тел
Сила, вызывающая сжатие пружины на величину y при нагружении ее силой F пр , определится через жесткость пружины [Н/м]
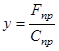 . (41)
. (41)
Если загрузить пружину статической силой, соответствующей массе падающего груза 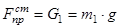 , то перемещение пружины в этом случае
, то перемещение пружины в этом случае
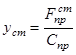 . (42)
. (42)
В случае динамической нагрузки, при падении тела массой m 1 с высоты h, перемещение пружины будет больше
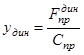 . (43)
. (43)
Разделив (43) на (42), получим значение динамического коэффициента
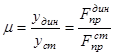 . (44)
. (44)
// Отношение динамического значения некоторого фактора (усилия, напряжения, перемещения) к соответствующему статическому значению этого фактора называется динамическим коэффициентом. //
Задача заключается в определении удин и m . Для этого применим теорему, согласно которой приращение кинетической энергии системы равно работе внешних сил. Запишем эту теорему для двух состояний системы – в начальный момент (у=0) и в момент максимального перемещения (у=удин):
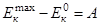 , (45)
, (45)
Кинетическая энергия системы в момент торможения 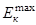 =0
=0
Кинетическую энергию в начальный момент найдем из следующих условий.
Скорость падающей массы найдем из условия сохранения энергии Ек=Еп  Þ
Þ 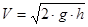 .
.
Начальную скорость движения системы тел найдем из закона сохранения количества движения 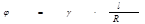 Þ
Þ 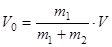 .
.
Кинетическая энергия системы в начале движения
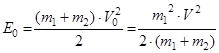 (46)
(46)
Работа внешних сил А будет равна разности работ сил тяжести (G1+G2) и работы силы пружины F пр.
Работа сил тяжести - 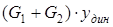
Работа силы пружины - 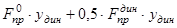

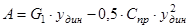 . (47)
. (47)
Подставляя (46) и (47) в (45)
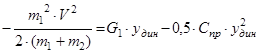 / (
/ ( 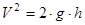 )
)
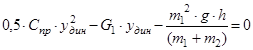 / (
/ (  )
)
 / : G1 (G1=m1×g)
/ : G1 (G1=m1×g)
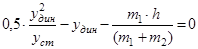 / * 2×y ст
/ * 2×y ст
 , решаем квадратное уравнение относительно y дин
, решаем квадратное уравнение относительно y дин
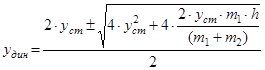
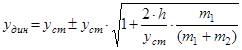 (знак «+» соответствует крайнему нижнему положению) (48)
(знак «+» соответствует крайнему нижнему положению) (48)
Используя формулу (44) получим выражение для динамического коэффициента
 , (49)
, (49)
обозначив 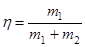 - коэффициент, учитывающий соотношение ударяемой m2 и ударяющей m1 масс, получим
- коэффициент, учитывающий соотношение ударяемой m2 и ударяющей m1 масс, получим
 . (50)
. (50)
Из формулы (50) видно, что динамический коэффициент тем больше, чем меньше статическое перемещение y ст и ударяемая масса m2 .
Для горизонтально соударяемых тел, формула для динамического коэффициента приобретает такой вид
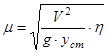 . (51)
. (51)
Таким образом, расчет на ударную прочность, зная динамический коэффициент, сводится к проверке условия
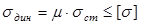 . (52)
. (52)
Лекция № 4
Дата добавления: 2018-09-23; просмотров: 321; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
