Главная обратная связь по состояниям. Метод модального управления
Пусть система S описывается уравнением:
.
Требуется найти такое управление u(t), что оно переводит систему из некоторой начальной точки 
в начало координат 0n, то есть 
.
Будем искать управление u(t) в виде
(1)
– это главная обратная связь по состояниям. Подставим эту функцию в исходное уравнение. Получим
.
Для оценки устойчивости этой линейной системы воспользуемся первым методом Ляпунова. Согласно первому методу Ляпунова, у матрицы 
все собственные числа должны быть отрицательны. Зададим некоторые собственные числа l1,…,ln<0 для этой матрицы и из ее характеристического полинома найдем числа k1,…,kn, составляющие вектор 
. Мы сможем найти вектор 
в случае, если система S полностью управляема.
Таким образом, введя модальное управление вида (1), можно обеспечить любое заданное распределение корней характеристического уравнения матрицы 
.
Методику нахождения модального управления лучше всего пояснить на примере.
Пример: требуется найти управление, переводящее систему
в состояние 
.
Управление будем искать в виде
;
Подставим это управление в исходное уравнение. Получим
.
.
Найдем характеристический полином этой матрицы:
. (2)
Зададим корни характеристического уравнения такими: 
. Теперь, если мы подставим их в характеристическое уравнение, мы получим одно уравнение с двумя неизвестными.
Поступим иначе: составим характеристический полином, корнями которого будут 
и 
:
|
|
|
.
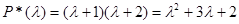Однако полином (2) имеет те же самые корни, что и последний полином, следовательно, мы записали одно и то же, то есть
.
Два полинома равны, если равны коэффициенты при соответствующих степенях независимой переменной (в данном случае l). Получим систему уравнений:
Отсюда находим, что 
. Следовательно, искомое управление будет иметь вид:
.
Асимптотический наблюдатель Люенбергера
Рассмотрим систему
(1)
Если эта система полностью наблюдаема, то можно построить такое устройство, которое называется асимптотический наблюдатель Люенбергера, на выходе которого получим оценку вектора состояния:
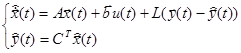, (2)
где 
– так называемая невязка между выходом и наблюдением; 
– полученная оценка состояния и выхода.
Назовем вектором ошибки разность между состоянием системы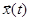 
и его оценкой 
:
.
Вычтем из первого уравнения системы (1) первое уравнение системы (2). Получим
.
Если (A–LCT) – гурвицева матрица, то 
, и значит 
.
Матрица 
будет или не будет гурвицевой в зависимости от матрицы L. То есть, мы можем обеспечить любое заданное распределение корней характеристического уравнения матрицы 
, задавая матрицу L.
|
|
|
Пример: найти L для системы
для корней характеристического уравнения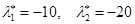 
.
Решение: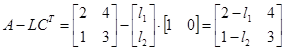 
.
Составим характеристические полиномы:
Корни этих полиномов должны быть равны, поэтому приравниваем коэффициенты при соответствующих степенях:
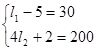
Отсюда получим, что 
.
Чтобы 
, необходимо, чтобы у гурвицевой матрицы 
главные диагональные миноры были положительными. Проверим это:
Значит, 
.
Список литературы
1. Математические основы теории автоматического регулирования, т. 1. Под ред. Б. К. Чемоданова. М., 1977
2. Справочное пособие по теории систем автоматического регулирования и управления. Под ред. Е. А. Санковского. Минск, 1973.
3. Воронов А. А. Введение в динамику сложных управляемых систем.
Дата добавления: 2018-09-22; просмотров: 225; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!