Устойчивость линейных систем с постоянными коэффициентами

Рассмотрим устойчивость линейной однородной системы дифференциальных уравнений с постоянными коэффициентами:

где A – квадратная матрица постоянных коэффициентов, 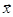– вектор-столбец неизвестных функций.

Пусть l1,…,lk – различные корни характеристического уравнения det(A–lE)=0, а e1,…,ek – максимальные показатели степени элементарных делителей, соответствующих этим корням. Решение исходной системы имеет вид:

причем Pi(t) – вектор-столбец, элементами которого являются многочлены от t; степень этих многочленов не превышает ei–1.

Для устойчивости линейной однородной системы дифференциальных уравнений с постоянными коэффициентами необходимо и достаточно, чтобы корни характеристического уравнения системы имели неположительные вещественные части, причем элементарные делители, соответствующие корням характеристического уравнения с нулевой вещественной частью, были бы простыми. Из этой теоремы следует, что линейная система с постоянными коэффициентами будет устойчивой и в случае кратных корней характеристического уравнения, лежащих на мнимой оси плоскости l, только этим корням должны соответствовать простые элементарные делители, то есть соответствующая клетка Жордана должна состоять из одного элемента.

Рассмотрим устойчивость линейного дифференциального уравнения n-го порядка с постоянными коэффициентами:

Характеристическое уравнение:

Это характеристическое уравнение имеет корень li кратности ei.

Для устойчивости линейного дифференциального уравнения n-го порядка с постоянными коэффициентами необходимо и достаточно, чтобы корни характеристического уравнения имели неположительные вещественные части, причем корни с нулевой вещественной частью должны быть простыми.

Для асимптотической устойчивости линейной системы дифференциальных уравнений с постоянными коэффициентами необходимо и достаточно, чтобы вещественные части корней характеристического уравнения были отрицательны, то есть характеристические числа матрицы A должны располагаться в левой полуплоскости.

Критерии устойчивости линейных систем

Критериями устойчивости называются правила, позволяющие исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения. Математически все формы критериев устойчивости эквивалентны, так как они определяют условия, при которых корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости корней.

Одним из таких критериев является критерий Гурвица – это алгебраический критерий, позволяющий в аналитической форме связать условия устойчивости с параметрами системы и выделить области устойчивости.

Этот критерий заключается в следующем: если характеристическое уравнение n-ой степени имеет вид

D(p)=cnpn+cn-1pn-1+…+c1p+c0=0,

то для устойчивости системы необходимо и достаточно, чтобы при cn>0 все n определителей Гурвица D1, D2, …, Dn, составленные по определенной схеме, были положительны.

Определители Гурвица составляются с помощью таблицы:

по правилам:

1) выписываются по диагонали все коэффициенты характеристического уравнения, начиная с cn-1;

2) заполняются горизонтальные строки – справа от данного коэффициента записываются коэффициенты с возрастающими индексами, а слева – с убывающими. В строках, где индекс коэффициентов меньше нуля или больше n, ставятся нули;

3) соответствующий определитель Di получится отчеркиванием i-ой строки и i-го столбца.

Для устойчивости системы необходимо и достаточно выполнение условий:

и т. д.

Необходимым условием устойчивости является положительность всех коэффициентов характеристического уравнения, то есть ci>0, i=1,2,…,n.

Пример: исследовать устойчивость решений линейной однородной системы с постоянными коэффициентами:

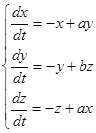
Характеристическое уравнение этой системы:

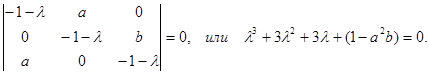
Матрица Гурвица имеет вид:

Определители Гурвица:

D1=3>0, D2=9–(1–a2b), D3=D2×(1–a2b).

Таким образом, для положительных главных диагональных миноров матрицы Гурвица требуется, чтобы параметр b удовлетворял неравенствам:

Еще одним критерием, позволяющим исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения, является критерий Рауса – это алгебраический критерий, позволяющий судить об устойчивости системы по коэффициентам характеристического уравнения. Особенно удобен он в тех случаях, когда эти коэффициенты заданы численно, а степень характеристического уравнения высока и использование критерия Гурвица затруднительно.

Критерий Рауса заключается в следующем – для устойчивости системы необходимо и достаточно, чтобы все коэффициенты первой графы таблицы Рауса были положительными.

Таблица Рауса для характеристического уравнения вида

D(p)=cnpn+cn-1pn-1+…+c1p+c0=0

составляется следующим образом:

1) в первой и второй строках таблицы выписываются соответственно коэффициенты cn,
cn-2,… и cn-1, cn-3,…;

2) для определения коэффициента aki таблицы нужно из (k+1)-го коэффициента (i-2)-ой строки (ak+1,i-2) вычесть произведение множителя ri-3 на (k+1)-й коэффициент (i-1)-ой строки (ak+1,i-1), то есть aki=ak+1,i-2–ri-3×ak+1,i-1. Множитель ri-3 есть отношение первого коэффициента (i-2)-й строки (a1,i-2) к первому коэффициенту (i-1)-й строки (a1,i-1). Он постоянен для каждой строки.

i k		1	2	3
1	Коэффициенты	cn	cn-2	cn-4
2	ri	cn-1	cn-3	cn-5
3		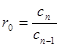a13=cn-2–r0cn-3	a23=cn-4–r0cn-5	a33=cn-6–r0cn-7
4		a14=cn-3–r1a23	a24=cn-5–r1a33	a34=cn-7–r1a43
5		a15=a23–r2a24	a25=a33–r2a34	a35=a43–r2a44
…	…	…	…	…

Для устойчивости системы должно выполняться условие:

cn>0, cn-1>0, a13>0, a14>0, …, a1,n+1>0.

Пример: задано характеристическое уравнение

D(p)=0.104p7+0.33p6+5.5p5+15.5p4+25p3+25p2+19.7p+9.5=0

Определим устойчивость системы. Для этого построим таблицу Рауса:

Коэффициенты	an=0.104	an-2=5.5	an-4=25	an-6=19.7
ri	an-1=0.33	an-3=15.5	an-5=25	an-7=9.5
r0=0.315	0.6	17.1	1.7	0
r1=0.55	6.0	15.8	9.5	0
r2=0.1	15.52	15.75	0	0
r3=0.386	9.7	9.5	0	0
r4=1.6	0.55	0	0	0
r5=0	9.5	0	0	0

Все коэффициенты первой графы положительны, следовательно, система устойчива

Второй метод Ляпунова

Второй, или прямой, метод Ляпунова позволяет исследовать устойчивость решений нелинейных дифференциальных уравнений, не производя решения самих уравнений. Мы будем исследовать устойчивость тривиального решения автономных систем дифференциальных уравнений, то есть систем уравнений вида

(1)

При этом мы предполагаем, что функции fi(x1,…,xn) имеют непрерывные частные производные по всем аргументам в некоторой выпуклой области G: <H n-мерного пространства. В этом случае в области G система уравнений (1) удовлетворяет условиям теоремы существования и единственности решения.

Рассмотрим функции V(x1,…,xn), определенные и непрерывные в области G: 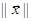<H и обладающие в этой области непрерывными частными производными по всем своим аргументам.

Функция V(x1,…,xn) называется знакоположительной (знакоотрицательной) в указанной области G, если для любого .

Функция V(x1,…,xn) называется положительно определенной (отрицательно определенной) в той же области G, если для любого , причем тогда и только тогда, когда =0.

Функции V(x1,…,xn) первого типа называют знакопостоянными, второго типа – знакоопределенными.

Достаточно просто определяется знакоопределенность в том случае, если функция V(x1,…,xn) представляет собой квадратичную форму, то есть

Тогда функция V(x1,…,xn) является положительно определенной, если положительно определена вышеуказанная квадратичная форма.

Дадим знакоопределенной функции V(x1,…,xn) геометрическую интерпретацию. Рассмотрим функцию двух переменных V(x1,x2). На плоскости x1, x2 линия V(x1,x2)=с (c – некоторое число) представляет собой замкнутую кривую, содержащую внутри себя начало координат (рис. 3). При c=0 кривая стягивается в начало координат.

Пусть si(t) – некоторое решение системы (1), удовлетворяющее начальным условиям si(t0)=xi0.

Полной производной по времени t функции V(x1,…,xn) в силу системы (1) называется функция

или, учитывая формулу полной производной,

Из этой формулы следует, что производная в силу системы (1) не зависит от выбранного решения s(t), а является функцией точки . Иначе полученное выражение можно записать так:

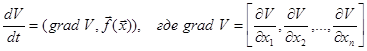Производная представляет собой скалярное произведение вектора на вектор фазовой скорости . При >0 фазовые траектории системы (1) пересекают поверхность в сторону возрастания , а при <0 – в сторону убывания.

Положительно определенные функции 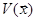, производные которых в силу системы (1) являются отрицательно определенными или знакоотрицательными, называются функциями Ляпунова.

Теорема Ляпунова об устойчивости гласит, что если для системы уравнений (1) существует положительно определенная функция , производная которой в силу системы (1) знакоотрицательна, то тривиальное решение системы (1) устойчиво по Ляпунову.

Пусть для системы дифференциальных уравнений (1) существует положительно определенная функция , производная которой в силу системы (1) отрицательно определена. Теорема Ляпунова об асимптотической устойчивости гласит, что тогда тривиальное решение системы (1) асимптотически устойчиво по Ляпунову.

Теорема Ляпунова о неустойчивости утверждает, что если для системы уравнений (1) существует непрерывная функция , удовлетворяющая условию , производная которой в силу системы (1) знакоопределенная, причем в любой окрестности начала координат имеются точки, в которых знак функции совпадает со знаком ее производной, то тривиальное решение системы неустойчиво в смысле Ляпунова.

Дата добавления: 2018-09-22; просмотров: 1826; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!