Исследование устойчивости нелинейных систем с помощью второго метода Ляпунова
Рассмотрим анализ устойчивости состояния равновесия некоторого класса нелинейных систем автоматического регулирования с помощью второго метода Ляпунова. Полагаем, что нелинейная САР состоит из линейного объекта регулирования и нелинейного регулятора. Поведение объекта регулирования описывается линейной системой дифференциальных уравнений с постоянными коэффициентами, которая в векторной записи имеет вид:
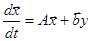, (1)
где 
– вектор координат, характеризующих состояние объекта регулирования;
y – скалярная координата, характеризующая воздействие регулятора на объект регулирования (регулирующее воздействие).
Матрица А полагается невырожденной (det A 
Регулятор имеет в своём составе сервомеханизм, управление которого
(2)
и чувствительный момент, формирующий сигнал ошибки
, (3)
где 
– вектор постоянных коэффициентов; r – скалярный параметр обратной связи. Относительно нелинейной функции 
будем полагать, что 
, 
если e¹0. В точке e=0 допускается разрыв непрерывности первого рода, функция f(e) предполагается непрерывной при e¹0.
Введем следующую классификацию рассматриваемых нелинейных САР в зависимости от характера корней характеристического уравнения матрицы A. САР будет:
1) собственно устойчива, если все корни характеристического уравнения матрицы A имеют отрицательные вещественные части, то есть Re li<0;
2) нейтральна по координатам x1,…,xk, если Re l1=Re l2=…=Re lk=0, а остальные корни имеют отрицательные вещественные части;
|
|
|
3) собственно неустойчива, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть.
Рассмотрим случай, когда корни характеристического уравнения матрицы A простые и удовлетворяют условию Re li≤0, i=1,2,…,n. Определим состояния равновесия, которые могут быть в нелинейной САР, описываемой уравнениями (1)–(3). Эти состояния равновесия представляют собой решения системы линейных алгебраических уравнений
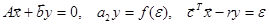(4)
Рассмотрим вспомогательную систему уравнений:
. (5)
Пусть определитель этой системы не равен нулю:
. (6)
В этом случае эта система уравнений имеет единственное решение, которое мы найдем по правилу Крамера:
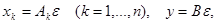(7)
.
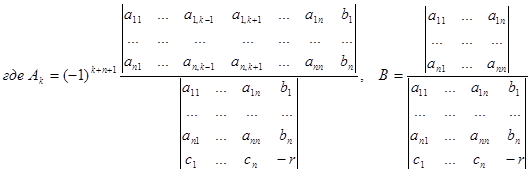Если a2=0, то из второго уравнения системы (4) следует, что e=0, и, согласно равенствам (7) получаем xk=0 (k=1,…,n) и y=0. Таким образом, система дифференциальных уравнений (1)–(3) имеет единственное состояние равновесия с координатами
xk=0, y=0 (k=1,…,n). (8)
Если a2¹0, то система уравнений (4) может иметь несколько решений. Из (7) и (4) следует
(9)
Это уравнение может иметь различные решения в зависимости от знака величины Ba2 и формы кривой f(e). Если Ba2<0, то уравнение (9) имеет единственное решение e=0, и система уравнений (4) имеет решение (8). Если Ba2>0, то уравнение (9) может иметь несколько решений. Обозначим их e1, …, em; тогда система (4) имеет m решений, определяемых равенствами
|
|
|
xki=Akei (k=1,…,n), yi=Bei (i=1,…,m). (10)
Таким образом, в зависимости от вида нелинейной функции f(e) и значений a2 и B в САР возможны следующие виды состояния равновесия:
1) Единственное состояние равновесия (8);
2) Конечное число состояний равновесия (10).
Исследование устойчивости любого из состояний равновесия (10) может быть сведено к рассмотрению устойчивости тривиального решения (8).
Пусть a1=1, a2=0. Тогда
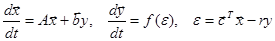. (11)
Исследование устойчивости тривиального решения системы (11) удобно проводить, когда уравнения приведены к канонической форме. Канонической формой уравнений (11) назовем такой их вид, когда матрица A приведена к жордановой форме. Для любой числовой матрицы A существует такая невырожденная матрица T, что T-1AT=J, где J – жорданова форма матрицы A.
Сделаем в системе (11) замену переменных:
Тогда из (11):
или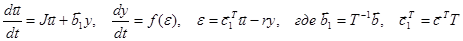 
.
Пусть 
, тогда
. (12)
Эта система уравнений является канонической формой уравнений движения. Мы рассматриваем случай простых корней характеристического уравнения матрицы A, поэтому J=diag A.
|
|
|
Для того, чтобы состоянию равновесия xk=0, y=0 системы уравнений (11) соответствовало единственное состояние равновесия zk=0, e=0 последней системы уравнений, требуется, чтобы определитель системы (12) был отличен от нуля, то есть
.
Учитывая, что J-1=T-1A-1T, 
, получаем:
.
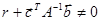Исследуем устойчивость тривиального решения системы уравнений (12), приведенной к канонической форме. Для исследования построим функцию Ляпунову специального вида, предложенную А. И. Лурье, с помощью этой функции найдем условия, накладываемые на параметры регулятора, при выполнении которых тривиальное решение систем (12) и (11) асимптотически устойчиво.
Пусть все корни характеристического уравнения det(A–lE)=0 простые и лежат в левой полуплоскости, то есть Re li<0, i=1,2,…,n. Функцию Ляпунова будем искать в виде
.
Чтобы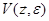 
была положительно определенной, требуется, чтобы первое слагаемое представляло собой положительно определенную квадратичную форму, тогда первое слагаемое будет строго положительным для всех 
, удовлетворяющих условию 
. Второе слагаемое в силу условий, накладываемых на функцию f(e), будет строго положительной для всех e, удовлетворяющих условию e¹0. Таким образом, функция 
будет определенно положительной, если квадратичная форма 
положительно определена.
|
|
|
Составим полную производную функции 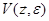по времени t в силу (12):
Так как B – симметрична, то BT=B, получим
.
Заменим C=–(JTB+BJ). Матрица С симметрична, поэтому
Видно, что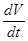 
является квадратичной формой относительно z1,…,zn, f(e). Если характеристические числа матрицы A удовлетворяют условию lj+li¹0, то по заданной симметричной матрице C однозначно определяется матрица B:
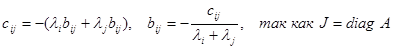. (13)
Пусть матрица A устойчива, то есть ее характеристические числа лежат в левой полуплоскости. Существует теорема, которая утверждает, что если С – матрица некоторой положительно определенной квадратичной формы, то определенная по формуле (13) матрица B также является матрицей положительно определенной квадратичной формы.
Получим условия, накладываемые на параметры САР для того, чтобы функция была функцией Ляпунова. Возьмем некоторую матрицу C положительно определенной квадратичной формы, тогда матрица B тоже будет матрицей некоторой положительно определенной квадратичной формы. Для того, чтобы функция 
была функцией Ляпунова, требуется, чтобы ее производная 
в силу системы (12) была отрицательно определенной функцией. Для положительной определенности функции –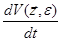 
требуется, согласно критерию Сильвестра, положительность всех главных диагональных миноров матрицы квадратичной формы. Так как матрица C положительно определенная, то первые n неравенств критерия выполняются, и остается одно:
Это условие является необходимым и достаточным условием отрицательной определенности производной 
. Перепишем его в виде
. (14)
Согласно второй теореме об асимптотической устойчивости состояний равновесия zk=0, e=0 системы (12) будет асимптотически устойчиво. При выполнении неравенства 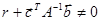(см. выше), получим, что
. (15)
Это будет означать асимптотическую устойчивость тривиального решения xk=0, y=0 системы уравнений (11). Таким образом, неравенства (14) и (15) являются достаточным условием асимптотической устойчивости состояния равновесия системы (11).
Когда характеристическое уравнение матрицы A имеет один нулевой корень, то выделим компоненту z1 вектор-функции 
в виде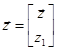 
. Тогда система (12) запишется в виде:
где 
– (n-1)-мерная вектор-функция, J’ – диагональная матрица порядка (n-1)x(n-1),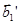 
и 
– (n-1)-мерные вектор-столбцы, b0 и c0 – скалярные величины. Функцию Ляпунова будем искать в виде
.
Если квадратичная форма 
является положительно определенной и a>0, то функция 
будет положительно определенной в пространстве 
.
Для того чтобы выражение в фигурных скобках представляло собой отрицательно определенную квадратичную форму, необходимо и достаточно, чтобы
Если b0c0<0, то можно подобрать такое положительное a, чтобы выполнялось равенство
.
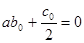Тогда производная будет знакоотрицательной функцией.
Дата добавления: 2018-09-22; просмотров: 425; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!