Экспоненциальная устойчивость
Пусть свободное движение системы S описывается уравнением
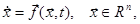(1)
где функция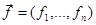 
определена, непрерывна и дифференцируем на некотором открытом множестве
Полагаем, что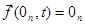 
, то есть существует равновесие 
, а в области определения 
выполняются неравенства:
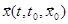– решение данной системы при начальных условиях 
. Равновесие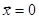 
называется экспоненциально устойчивым, если для любых значений из области ||x0||<r, t0>0 можно выбрать такие два положительные числа M и a, что для всех t>t0 справедливо неравенство:
. (2)
Кривая 
будет мажорантой для кривой 
.
Согласно теореме Красовского, если каждое решение 
системы (1) удовлетворяет условию (2) экспоненциальной устойчивости положения равновесия 
, то в области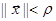 
существует функция Ляпунова 
, такая, что ее полная производная по времени 
в силу уравнений движения 
имеет знак, противоположный знаку V. Функция V удовлетворяет оценкам:
, (3)
где с1, c2, c3, c4 – вещественные числа, 
.
Условия теоремы всегда выполняются для линейных стационарных асимптотически устойчивых систем, и в этом случае функция Ляпунова не зависит от t и представляет собой квадратичную форму
,
При t®¥ в устойчивой свободно движущейся системе с функцией Ляпунова вида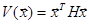 
и, следовательно, функция Ляпунова V также стремится к нулю. Из (3) следует, что
.
Заменим во втором неравенстве из (3) правую часть 
большой величиной 
. Неравенство усилится:
|
|
|
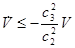. (5)
Это линейное дифференциальное неравенство, на основе которого можно получить мажоранту и построить мажорирующую модель сравнения.
. (5a)
Это уравнение, соответствующее предыдущему неравенству или порожденное неравенством. Решение этого уравнения имеет вид:
. (6)
Представим полученное решение в виде равенства:
,
где d(t) – неизвестная функция времени, о которой можно сказать лишь то, что она неотрицательна для всех t³t0, для которых выполняется (5). Тогда решение:
.
Поскольку d(t) положительна, получим неравенство
. (7)
Если выбрать V0=z0, правая часть этого неравенства становится равной решению (6), и мы получим:
.
Заменим в правой части (7) V0 на бόльшую величину 
, а в левой V(t) – на меньшую 
:
. (8)
Извлекая из обоих частей квадратный корень, получим линейное относительно 
неравенство
.
Таким образом решение z(t) уравнения (5a), определяемое (6), будет мажорировать:
а) функцию Ляпунова V(t), если V(t0)≤z0, что следует из (7) и (6);
б) функцию квадрата нормы переменной состояния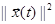 
, если 
, что вытекает из (8) и (6).
Поскольку матрица H положительно определенная , то все ее собственные значения вещественны и положительны, и мы можем выразить через них c1 и c2:
|
|
|
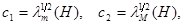(9)
где lm(H) – наименьшее, а lM(H) – наибольшее из собственных значений матрицы H. Далее
.
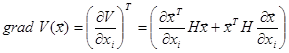Так как H – симметрична, то
,
Отсюда
, или 
(10)
При этом в (9)–(10) было использовано свойство симметрических вещественных матриц:
. (11)
Наибольшее lM(H) и наименьшее lm(H) собственные значения матрицы H, если H положительно определена, будут вещественными и положительными.
Таким образом для функции 
, независимо от вида (1) и (3) можно записать:
Коэффициент 
будет зависеть от вида уравнения.
Для линейной стационарной системы
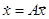
имеем
.
Обозначим 
, где G – положительно определенная симметрическая матрица. Следовательно,
,
то есть в данном случае 
также является квадратичной формой, и на основании (11) можно записать
.
Таким образом, для квадратичных функций Ляпунова и для корней квадратных из них в случае стационарной системы все коэффициенты в неравенствах (3) Красовского выражены через собственные значения матриц H и G.
Дата добавления: 2018-09-22; просмотров: 362; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!