Вероятности суммы и произведения случайных событий.

Формула полной вероятности, Байесса, Бернулли и Пуассона.

Венцель Е. С. Гл.3, Гл.4.

Гмурман В. Е. Гл.2, гл.3, гл.4. гл.5 §1.

Роднищев Н.Е. Гл. 2.

При проработке данного раздела, прежде всего, необходимо твердо уяснить такие понятия как сумма и произведение событий. Следует иметь в виду, что формулы для определения вероятностей суммы и произведения событий являются основными для дальнейшего изложения теории вероятностей. Они позволяют по известным вероятностям одних событий вычислить вероятность других событий. По указанной литературе изучить выводы формул для вероятности суммы несовместных и совместных событий, для вероятности произведения независимых и зависимых событий. Путем решения ряда задач приобрести навыки по применению формул для суммы и произведения событий.

Важным для практических приложений теории вероятностей являются формула полной вероятности и формула Байесса, а также формула Бернулли и Пуассона для повторных независимых испытаний, которые получаются с использованием предыдущих результатов. Следует уяснить круг задач, требующих применения указанных формул.

Вопросы для самопроверки: Роднищев Н.Е. стр. 34.

Вопросы для самопроверки:

1. Что такое сумма случайных событий и как она определяется в случаях совместных и несовместных событий?

2. Чему равна вероятность суммы несовместных и совместных событий?

3. Как определяется вероятность суммы событий, образующих полную группу событий?

4. Пояснить что такое условная вероятность события? Какие события называются независимыми?

5. Приведите формулы для вероятности независимых и зависимых событий.

6. Как определяется вероятность появления хотя бы одного из совокупности событий?

7. Что позволяет определять формула полной вероятности?

8. Какой смысл имеет условная вероятность, определяемая по формуле Байесса?

9. Приведите формулы Бернулли и Пуассона о повторении независимых испытаний и что они позволяют определить?

Примеры решения задач к части 1

Задача 1. В лаборатории работают 7 мужчин и 3 женщины. По табельным номерам в случайном порядке отобраны три человека. Определить вероятность того, что отобранные лица окажутся мужчинами.

Решение. Для нахождения искомой вероятности следует воспользоваться формулой, дающей классическое определение вероятности случайного события А: Р(А) = m/n, где n – число всех возможных элементарных исходов (совокупность единственно возможных и равновозможных исходов), m – число тех элементарных исходов, которые благоприятствуют событию A (m<n).

В данной задаче величина n может быть представлена как количество групп, которые можно составить из общего количества 10 человек по 3 человека в группе. В комбинаторике это число находиться как число сочетаний из 10 различных элементов группами по 3 элемента каждой: 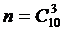. Очевидно, что 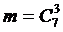, т. е. столько можно образовать из 7 мужчин групп по 3 мужчины в каждой. Таким образом, .

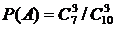Задача 2. Коэффициент использования рабочего времени двух автоматических станков соответственно равен 0,9 и 0,95. Считая, что остановки в работе каждого станка возникают случайно и независимо друг от друга, определить относительное время: а) совместной работы двух станков, б) работы только одного станка, в) простоя обоих станков.

Решение. Коэффициент использования рабочего времени – это отношение времени непосредственной работы станка ко всему рабочему времени (например, сменному). Оно совпадает с определением вероятности события, что станок в данный момент работает. Относительное время, которое необходимо определить, это также вероятности соответствующих событий.

Введем следующие события: 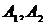- работа соответственно первого и второго станка, 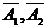- простой соответственно первого и второго станка (события, противоположные соответственно событиям 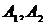), 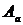- совместная работа двух станков, 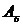- работа только одного станка, 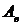- простой обоих станков.

По условию задачи имеем P(A₁) = 0,9; P(A₂)=0,95; P( 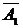)=1-P(A₁)=0,1; P( 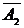)=1-P(A₂)=0,05.

a) Совместная работа станков – это работа и первого и второго станка вместе: 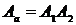. Поскольку события А₁, А₂ – независимые, вероятность произведения событий равняется произведению событий А₁, А₂:

P( 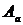) = P(A₁)P(A₂) = 0,9 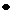0,95 = 0,855.

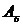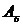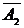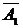б) Работа одного из станков имеет место тогда, когда первый станок работает, и второй не работает, или первый не работает и второй работает. Таким образом, событие можно определить так: = A₁ + A₂. Учитывая, что события 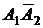и - несовместные, а каждая пара событи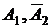й и 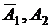независимые, запишем

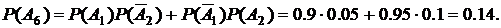
в) Простой обоих станков – это простой и первого и второго станков: 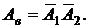События 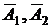- независимые. Искомая вероятность

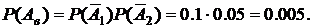
Задача 3. Станок-автомат штампует детали. Вероятность того, что за смену не будет изготовлено ни одной бракованной детали, равна 0,9. Определить вероятность того, что за три смены не будет изготовлено ни одной бракованной детали.

Решение. Обозначим через 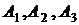- события, состоящие в том, что соответственно за первую, вторую и третью смены не будет изготовлено ни одной бракованной детали. Очевидно, что искомое событие A является произведением событий 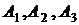: 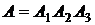, так как событие A наступает при условии наступления 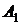и 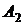, и , и 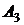. Отметим, что события 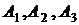– независимые, ибо вероятности наступления каждого из этих событий равны 0,9 и не зависят от того, имели место два других события или нет. Вероятность произведения независимых событий равна произведению вероятностей отдельных событий.

Следовательно,

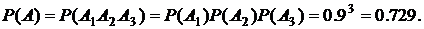
Задача 4. Рабочий обслуживает три станка, работающие независимо друг от друга. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,92, для второго станка такая вероятность равна 0,9 и для третьего – 0,85. Какова вероятность того, что в течение часа хотя бы один станок не потребует внимания рабочего?

Решение. Обозначим через A событие, выражающее то, что в течение часа хотя бы один станок не потребует внимания рабочего, а через 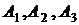обозначим, соответственно, события, заключающиеся в том, что первый, второй и третий станки в течение часа не потребует внимания рабочего. Так как все три станка работают независимо друг от друга и могут потребовать внимания рабочего одновременно, то события 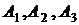являются независимыми, но совместными событиями. Согласно обозначениям имеем 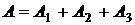и

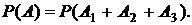
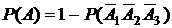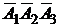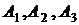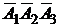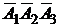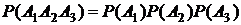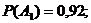
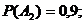
В данной задаче определение искомой вероятности целесообразно осуществить по формуле , где - события, состоящие в том, что соответственно первый, второй и третий станки потребуют внимания рабочего. Из независимости событий следует независимость событий . С учётом сказанного вероятность произведения событий запишется так: . По условию задачи 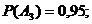. Вероятности соответствующих противоположных событий будут: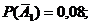 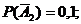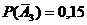. В результате вычислений находим .

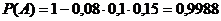Задача 5. В цехе три типа станков-автоматов производят одни и те же детали. Станков первого типа 5 штук, второго типа – 3, третьего типа – 2. Производительность станков одинаковая, а качество работы различное. Известно, что станки первого типа производят 94% деталей отличного качества, второго типа – 90% и третьего типа – 85%. Все произведенные в цехе детали в нерассортированном виде помещены в общий ящик.

Определить вероятность того, что случайно взятая деталь из ящика окажется отличного качества.

Решение. Задачи такого типа решаются с использованием формулы полной вероятности. Обозначим через A событие, состоящее в том, что случайно взятая деталь окажется отличного качества. Чтобы событие A могло произойти, необходимо, чтобы произошло одно из событий H₁, H₂, H₃, где H₁ – случайное событие, состоящее в том, что случайно взятая деталь была изготовлена на станке первого типа, H₂ – деталь была изготовлена на станке второго типа, H₃ – деталь была изготовлена на станке третьего типа.

Учитывая количественное соотношение станков разных типов в общем количестве десяти станков и то, что производительность станков каждого типа одинаковая, легко найти вероятность случайных событий H₁, H₂, H₃: P(H₁) = 5/10, P(H₂) = 3/10, P(H₃) = 2/10. Поскольку события H₁, H₂, H₃ являются полной группой событий, то сумма их вероятностей равна единице. По условию задачи находятся условные вероятности P(A/H₁), P(A/H₂), P(A/H₃), т.е. вероятности извлечения детали отличного качества из набора деталей, изготовленных соответственно первым, вторым и третьим типом станков: P(A/H₁) = 0,94; P(A/H₂) = 0,9; P(A/H₃) = 0,85.

По формуле полной вероятности

определяем: .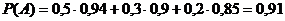

Задача 6. Повторяя условия предыдущей задачи, заключительный вопрос сформулируем иначе. Случайно извлеченная из ящика деталь оказалась деталью отличного качества. Какова вероятность, что эта деталь была изготовлена станком первого, второго, третьего типа.

Решение. Задачи такого типа решаются с использованием формулы Бейесса. Искомые вероятности определяются как условные вероятности событий H₁, H₂, H₃при условии, что событие A – извлечение детали отличного качества произошло.

Формулы Байесса применительно к данной задаче запишутся в виде:

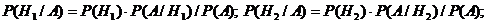
P(H₃/A) = P(H₃)P(A/H₃)/P(A),

где P(A) – вероятность события А, рассмотренная в предыдущей задаче и равная 0.91. В результате находим: P(H₁/A) = 0,5*0,94/0,91 = 0,516; P(H₂/A) = 0,3*0,9/0,91 = 0,297 P(H₁/A) = 0,2*0,85/0,91 = 0,187.

В заключение отметим, что условные события H₁ / A,H₂ / A, H₃ / A являются несовместными и образуют полную группу событий. Поэтому сумма найденных условных вероятностей равна единице.

Задачи к части

1. СЛУЧАЙНЫЕ СОБЫТИЯ

1. Партия из 100 деталей проверяются контролером, который наугад отбирает 10 деталей и проверяет их качество. Если среди выбранных контролером 10 изделий ни одного бракованного, то вся партия принимается. Какова вероятность того, что партия из 100 деталей, содержащая 10 бракованных, будет принята контролером?

Ответ: 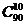/ 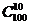= 0.331.

2. В ящике N деталей, из которых M стандартных. Найти вероятность того, что из K наугад извлеченных деталей не будет ни одной стандартной (K<N-M).

Ответ: /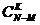

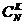
3. В ящике N деталей, из которых M стандартных. Найти вероятность того, что из K наугад извлеченных деталей будет хотя бы одна стандартная (K<N-M).

Ответ: 1-( / ).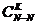

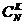4. Для контроля продукции из трех партий взята одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 1/3 деталей бракованных, а в двух других все стандартные?

Ответ: 1/9.

5. В ящике 30 изделий, из которых 20 первого сорта, 5- второго, 5- бракованных. Найти вероятность извлечения стандартного изделия?

Ответ: 5/6.

6. Вероятность того, что в течении одной смены возникнет неполадка станка, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за три смены?

Ответ: 0.857.

7. На двух автоматических станках изготавливаются одинаковые детали. Известно, что производительность первого станка в два раза больше, чем второго, и что вероятность изготовления детали высшего качества на первом равна 0.98, а на втором 0.94. Изготовленные за смену на обоих станках нерассортированные детали отправлены на склад. Определить вероятность того, что наугад взятая со склада деталь изготовлена на первом станке и окажется высшего качества.

Ответ: 0.633.

8. Вероятность безотказной работы блока, входящего в систему, в течение заданного времени составляет 0.8. Для повышения надежности устанавливают такой же резервный блок. Требуется найти, какой станет вероятность безотказной работы блока с учетом резервного (двух резервных).

Ответ: 0.96; 0.992.

9. Три электрические лампочки включены в цепь последовательно. Вероятность того, что одна (любая) лампочка перегорит, если напряжение в цепи превысит номинальное, равна 0.6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет.

Ответ: 0.936.

10. Работа прибора прекратилась вследствие выхода из строя одной лампы из общего числа N. Отыскание одной лампы производится путем поочередной замены каждой лампы новой. Определить вероятность того, что придется проверять, N ламп, если вероятность выхода из строя каждой лампы p.

Ответ: (1-p)^N^-1p.

11. В цехе три типа автоматических станков производят одни и те же детали. Производительность их одинакова, но качество работы различное. Известно, что станки первого типа производят 94% отличного качества, второго типа 90%, третьего типа-85%. Все произведенные в цехе за смену детали нерассортированными отправлены на склад. Определить вероятность того, что взятая наугад деталь не будет отличного качества, если станков первого типа 5, второго типа 3, третьего типа 2.

Ответ: 0.09.

12. Вероятность удовлетворить стандарту для изделий некоторого производства равна 0.9. Предлагается упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0.95 для изделий, удовлетворяющих стандарту, а для изделий, не удовлетворяющих стандарту, с вероятностью 0.15. Найти вероятность того, что изделие, признанное при упрощенной проверке стандартным, действительно удовлетворяет стандарту.

Ответ:0.98.

13. На телевизионном заводе на 40% телевизоров ставятся импортные кинескопы, а на 60%-отечественные. Вероятность того, что телевизор с импортным кинескопом не выйдет из строя из-за отказа кинескопа в течение гарантийного срока равна 0.98, а аналогичная вероятность для телевизоров с отечественным кинескопом равна 0.82. Купленный телевизор не вышел из строя из-за отказа кинескопа в течение гарантийного срока. Какова вероятность того, что это был телевизор с импортным кинескопом?

Ответа: 98/221.

14. На телевизионном заводе на 40% телевизоров ставятся импортные кинескопы, а на 60%-отечественные. Вероятность того, что телевизор с импортным кинескопом не выйдет из строя из-за отказа кинескопа в течение гарантийного срока равна 0.98, а аналогичная вероятность для телевизоров с отечественным кинескопом равна 0.82. Купленный телевизор не вышел из строя из-за отказа кинескопа в течение гарантийного срока. Какова вероятность того, что это был телевизор с отечественным кинескопом?

Ответ: 123/221.

15. Некоторый аэропорт в среднем 15% осенних дней закрыт. Какова вероятность того, что на одной неделе осени аэропорт будет закрыт а) два дня б) три дня в) не более 4-х дней?

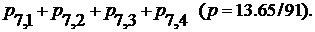Ответ: а) 0.21; б) 0.062; в)

16. Вероятность изготовления стандартной детали равна 0.95. Какова вероятность того, что среди 10 деталей не более одной стандартной?

Ответ: 0.914.

17. Станок-автомат изготавливает детали, каждое из которых с вероятностью 0.01 имеет дефект. Каков должен быть объем случайной выборки (с возращением), чтобы вероятность встретить в ней хотя бы одну дефектную деталь была не менее 0.95?

Ответ: n>=300.

18. Предприятие отправило 5000 доброкачественных изделий автотранспортом. Вероятность повреждения изделия в пути 0.0002. Найти вероятность того, что в пункт назначения прибудет 3 поврежденных изделия из 5000.

Ответ: 0.06.

19. Из партии деталей, среди которых N стандартных и M бракованных, для контроля случайно взято S штук. При контроле оказалось, что первые К деталей из S оказались стандартными. Определить вероятность того, что следующая деталь будет стандартной.

Ответ: (N-K)/(N+M-K).

20. В трех ящиках находятся однотипные изделия: в первом 10 изделий, из них 3 бракованных, во втором 15 изделий, из них 5 бракованных, в третьем 20 изделий, из них 6 бракованных. Случайно извлекается одно изделие и оно оказалось бракованным. Определить вероятность того, что это изделие было извлечено из второго ящика.

Ответ: 5/14.

21. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружение бракованной продукции, если в одной партии 2/3 деталей бракованные,

а в двух других – все доброкачественные?

Ответ:2/9.

22. Участок электрической цепи, представляет собой последовательное соединение одного элемента с двумя другими, которые сами соединены параллельно. Вероятность выхода из строя каждого элемента за определенное время равна 0.2. Какова вероятность разрыва цепи за указанное время?

Ответ:0,232.

23. В ящик, содержащий 3 одинаковые по внешнему виду детали, брошена стандартная деталь. Найти вероятность того, что будет извлечена стандартная деталь, если вероятны все возможные предположения о числе стандартных деталей, первоначально находившихся в ящике.

Ответ: 0,625.

24. Вычислительный центр, который должен производить непрерывную обработку поступающей информации, располагает двумя вычислительными установками. Известно, что каждая из них имеет вероятность отказа 0,2 за некоторое время. Определить вероятность: а)того, что откажет одно из них, а второе будет исправно; б) безотказной работы каждого из устройств.

Ответ: а)0,32 б)0,64

25.На сборку агрегата поступают детали из трех автоматов. Первый автомат делает 20%, а второй 30% и третий 50% всех деталей, которые поступают на сборку. Первый автомат делает 0,2% брака, второй 0,3% и третий 0,1%. Найти вероятность того, что на сборку поступила бракованная деталь.

Ответ: 0,0018.

26. Рабочие на станке штампуют детали. Вероятность того, что в дневную смену не будет выпущено ни одной нестандартной детали, составляет 0,9, в вечернюю смену- 0,85, в ночную-0,8.Определить вероятность того, что за три смены не будет выпущено ни одной нестандартной детали.

Ответ: 0,612.

27. Имеется две партии изделий по 12 и 10 штук, причем в каждой партии одно изделие бракованное. Изделие, взятое наугад из первой партии, переложено во вторую, после чего выбирается наугад изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

Ответ: 13/132.

28. На складе имеются приборы, изготовленные тремя заводами: 20% приборов изготовлены заводом №., 50%- заводом №2, 30%- заводом №3. Вероятности того, что в течение года прибору потребуется ремонт для продукции каждого завода соответственно 0,2; 0,1; 0,3. Взятый со склада прибор не имел заводской маркировки и потребовал ремонта в течение года. Каким заводом вероятнее всего был изготовлен этот прибор? Какова вероятность?

Ответ: №3, 0,5.

29. У сборщика имеется 16 деталей, изготовленных первым заводом, И 4 детали, изготовленные вторым заводом. Случайно взяты две детали. Найти вероятность того, что хотя бы одна деталь окажется изготовленной первым заводом.

Ответ: 0,968.

30. В партии из 50 изделий 5 бракованных. Из партии выбираются наугад 6 изделий. Определить вероятность того, что среди этих 6 изделий 2 окажутся бракованными.

Ответ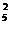: С 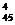С /С .

31. Имеется две партии изделий по 122 и 8 штук, причем в каждой партии одно изделие бракованное. Два изделия, взятые наугад, переложены во вторую партию, после чего выбирается наугад изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

Ответ: 7\60.

32. В двух ящиках находятся детали: в первом 10 (из них 3 стандартные), во втором – 15 (из них 6 стандартных). Из каждого ящика случайно вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.

Ответ: 0,12

33. При приемке партии из 80 изделий, среди которых 6 бракованных, проверяется 40 случайно выбранных изделий. Определить вероятность того, что партия будет принята, если условиями приема допускается бракованных изделий не более двух среди проверенных.

Ответ: 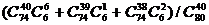=0,337.

34. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно равна 0,1. Найти вероятность того, что а) из трех проверяемых изделий только одно окажется стандартным, б) нестандартным окажется только четвертое по порядку проверяемое изделие.

Ответ: а) 0,243; б) 0,0729.

35. При приемке партии изделий подвергается проверке половина случайно отобранных изделий. Условия приемки – наличие брака в выборке не свыше 2%. Вычислить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.

Ответ: .

36. Предприятие изготовляет 95% изделий стандартных, причем из них 86% первого сорта. Найти вероятность того, что случайно извлеченное изделие окажется изделием первого сорта.

Ответ: 0,817.

37. В ремонтной мастерской по статистическим данным в среднем на 20 остановок токарного станка приходится: 10 – для смены резца, 3 – из-за неисправности привода, 2 – из-за несвоевременной подачи заготовки. Остальные остановки станка происходят по другим причинам. Найти вероятность остановки станка по другим причинам.

Ответ: 0,25.

38. В цехе 10 станков. Вероятность быть включенным для каждого станка равна 0,9. Найти вероятность того, что 5 станков будут работать одновременно.

Ответ: 0,0015.

39. При изготовлении деталей производится три технологические операции. Процент появления брака при каждой из них соответственно равен 0,2%; 0,3%; 0,1%. Определить вероятность получения детали высшего качества, если высшим качеством изготовляется 25% стандартных деталей.

Ответ: 0,2485.

40. На предприятии на 60% стиральных машин ставится импортный двигатель, а на остальные – двигатель собственного производства. Вероятность безотказной работы в течение гарантийного срока импортного двигателя 0,98, а двигателя собственного производства – 0,85. Найти вероятность того, что случайно выбранная при покупке стиральная машина не выйдет из строя в течение гарантийного срока из-за отказа двигателя.

Ответ: 0,928.

Часть 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

Дата добавления: 2018-08-06; просмотров: 4087; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!