Обобщенная логистическая популяция

Пусть динамика роста популяции описывается уравнением:

,                                                                  

где  удовлетворяет следующим условиям:

а)

б)

в)

Фазовый портрет имеет вид

Точка покоя  - неустойчивая, а точка покоя  - устойчивая.

 

Опасность жесткого планирования при эксплуатации экосистем

Рассмотрим обобщенную логистическую модель популяции рыб в озере или в мировом океане:

где 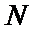 - количество рыб, причем пусть уравнение имеет точки покоя:

,

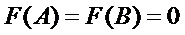гдеА=0, В=К.

Замечание. Вблизи точкиА=0, когда численность популяции мала, модель близка к модели Мальтуса.

С течением времени устанавливается стационарный режимВ=К.

1. Модель «жесткой» эксплуатации.

Рыболовство ведется с постоянной интенсивностью с(квота вылова) без учета численности популяции:

Пусть  достигает максимума в точке

а)Случай .

Система имеет два равновесных состояния:  и .

Состояние  устойчиво (аттрактор): популяция в этом случае несколько меньше, чем при  (нет рыболовства).

Если вследствие каких-либо причин (браконьерство, мор) размер популяции упадет хоть немного ниже уровня , то в дальнейшем популяция будет уничтожена полностью за конечное время.

б) Случай

Популяция уничтожается за конечное время, как бы велика она ни была вначале. Это – судьба бизонов, многих видов китов, белых тигров.

в) Случай

Это случай оптимальной квоты улова, при которой эксплуатируемая популяция еще не уничтожается, но доход максимален.

Точка покоя  - неустойчива (шунт). Небольшое случайное уменьшение численности ниже  приводит к полному уничтожению популяции за конечное время.

           В итогепри жестком планировании эксплуатация популяции приводит к полному уничтожению при любой квоте.

Фазовый портрет автономной линейной системы второго порядка

Рассмотрим систему

.                                                                                (1)

Положение равновесие:

                                                                                         

Если

,                                                                                        

точка (0;0) - единственная точка покоя системы.

Фазовые траектории определяются из уравнения

                                                     (2)

Преобразуем последнее уравнение при помощи линейной неособенной подстановки

, причем (3)

так, чтобы в новых переменных система имела наиболее простой вид.

Из аналитической геометрии известно, что вид уравнения (2) в новых переменных зависит от корней характеристического уравнения системы (1), т.е.

                                                                    (4)

Корни (4) называются собственными числами системы (1).

Анри Пуанкаре показал, что возможны следующие случаи, каждому из которых отвечает свое расположение фазовых кривых в окрестности точки покоя.

I. .

Система (1) приводится к виду

                                                                                             (5)

Различают четыре случая.

1)  - вещественные одного знака.

Точка покоя  называется узлом.

Вид фазовых траекторий:

устойчивый узел                                              неустойчивый узел

                                                                        

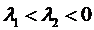
Пример.

Характеристическое уравнение (4) имеет вид:

имеет корни . Точка покоя – неустойчивый узел.

2)  - вещественные и противоположных знаков.

Точка покоя - седло. (неустойчивая точка покоя)

3)  - комплексно сопряженные: , , . Выделяем вещественные и мнимые части:

.

Точка покоя   - фокус.

устойчивый фокус                            неустойчивый фокус

                                                                                                 

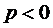
Пример.

Характеристическое уравнение (4) имеет вид:

.

имеет дискриминант  , откуда 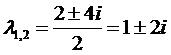. Точка покоя – неустойчивый узел.

 

4)  - чисто мнимые: , . Тогда фазовые траектории – окружности. Точка покоя - центр.

II. Корни характеристического уравнения кратные.

1) Кратные корни не равные нулю, причем .

Точка покоя - вырожденный узел.

2) Кратные корни не равные нулю, причем .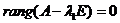

Точка покоя – дикритический узел.

Система «хищник – жертва».

 

Допущения:

1. Среда однородная.

2. Численность данного вида описывается одной переменной, т.е. мы пренебрегаем возрастными, половыми и генетическими различиями.

3. Пренебрегаем случайными флуктуациями.

4. Взаимодействие мгновенное.

 

Уравнения системы «хищник-жертва»

                                              (1)

Функция  определяется в экспериментальных работах. К настоящему времени установлено, что эти функции принадлежат к одному из следующих трех типов.

1)

Этот тип характерен для беспозвоночных и некоторых видов хищных рыб.

2)

Трофическая функция с резко выраженным порогом насыщения характерна для хищников - фильтраторов (моллюсков).

3)

Такой тип характерен для позвоночных – организмов, способных к обучению.

При малых значениях численности жертвы почти все жертвы становятся добычей хищника, который всегда голоден и насыщения не наступает. Трофическую функцию можно считать линейной:

22)Классическая модель Вольтерра:

                                                                        (2)

Начальные условия

                                                                                                      (3)

 

---

Дата добавления: 2018-08-06; просмотров: 254; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая1234567Следующая ⇒

---

Мы поможем в написании ваших работ!