Алгоритм обработки экспериментальных данных с помощью метода наименьших квадратов.
- Предварительная обработка данных. На этом этапе, как правило, осуществляется устранение помехи, действующей на объект и обусловленной случайными факторами, путем использования фильтров, например, скользящего среднего, метода четвертых разностей, экспоненциального фильтра и т.д. Случайная составляющая помехи встречается практически при любых измерениях.
- Собственно идентификация. Это определение параметров математической модели по экспериментальным данным. При этом вид математической модели (это может быть уравнение прямой, параболы или любая другая зависимость) выбирается заранее. Определение параметров в общем случае – это поиск минимума многомерной функции-критерия.
- Оценка результатов моделирования, т.е. оценка адекватности математической модели, которая состоит в определении степени соответствия математической модели данным эксперимента.
Как определяются коэффициенты регрессионных функций при линейном характере экспериментальных данных?
Будем искать приближающую функцию в виде:
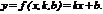
Абсолютная разность  для
для  определяется следующим образом:
определяется следующим образом:


формулу (10.2) перепишем в виде:

Рассматриваемая сумма является функцией с двумя параметрами  Задача сводится к отысканию минимума этой функции. Используем необходимое условие экстремума:
Задача сводится к отысканию минимума этой функции. Используем необходимое условие экстремума:

т.е. 
(10.3)
|
|
|

Решив систему двух уравнений с двумя неизвестными относительно параметров  и
и  , получим конкретный вид искомой функции
, получим конкретный вид искомой функции  Опуская математические выкладки, запишем выражения для искомых параметров:
Опуская математические выкладки, запишем выражения для искомых параметров:
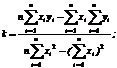 (10.4)
(10.4)
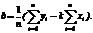
Рассчитав значение  , получим величину среднеквадратичной ошибки рассматриваемого приближения.
, получим величину среднеквадратичной ошибки рассматриваемого приближения.
Замечание: найденные значения  и
и 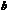 определяют точку экстремума
определяют точку экстремума  . Используя неравенство Коши-Буняковского можно доказать, что в этой точке функция принимает минимальное значение
. Используя неравенство Коши-Буняковского можно доказать, что в этой точке функция принимает минимальное значение
Как определяются коэффициенты регрессионных функций при гиперболическом характере экспериментальных данных?
Приближающая функция имеет вид
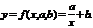 (10.20)
(10.20)
Для перехода к линейной функции сделаем подстановку 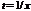 . Получим
. Получим 
Перед нахождением приближающей функции вида 10.20 значения аргумента в исходной таблице 10.1 необходимо заменить обратными числами и найти для новой таблицы 10.7 приближающую функцию в виде линейной регрессии (10.4).
|
|
|

Рис. 10.7 График гиперболической функции
Окончательно получим
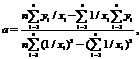 (10.21)
(10.21)

Как определяются коэффициенты регрессионных функций при экспоненциальном характере экспериментальных данных?
Показательная зависимость имеет вид
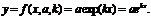 (10.8)
(10.8)
Во всех случаях  при
при  . Если
. Если  то при
то при  кривая растет с увеличением
кривая растет с увеличением  тем быстрее, чем больше
тем быстрее, чем больше  При
При  она приближается к оси абсцисс с возрастанием
она приближается к оси абсцисс с возрастанием  тем быстрее, чем больше абсолютная величина
тем быстрее, чем больше абсолютная величина 

Рис. 10.3 График показательной функции
 (10.9)
(10.9)
приняв обозначения  перепишем (10.9) в виде:
перепишем (10.9) в виде:
 (10.10)
(10.10)
|
|
|
Окончательно получаем:
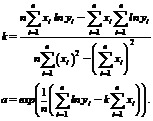 (10.11)
(10.11)
 Рис. 10.4
Рис. 10.4
Дата добавления: 2018-08-06; просмотров: 289; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
