Определение числа рейнольдса для каналов произвольного сечения.
34.
Распределение касательных напряжений и скоростей в ламинарном потоке.
Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром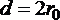 
. Чтобы исключить влияние силы тяжести и этим упростить вывод уравнений, расположим трубу горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался, выделим участок длиной 
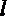между сечениями 1-1 и 2-2 (рис. 1.6.2).
|
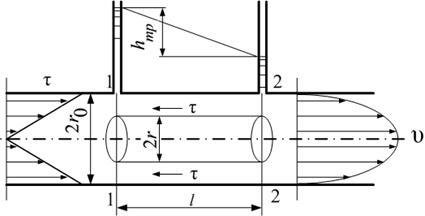
| Рис. 1.6.2. Распределение скоростей и касательных напряжений по сечению круглой трубы |
Пусть в сечении 1-1 давление равно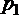 
, а в сечении2-2 - 
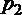. В цилиндрической трубе скорость жидкости будет постоянной, а коэффициент 
будет неизменным вдоль стабильного потока, тогда уравнение Бернулли для выбранных сечений примет вид (1.4.10)
,
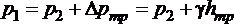где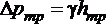 
- потеря давления на трение по длине трубы, определяемая по показаниям пьезометров, установленных в этих сечениях (см. рис. 1.6.2).
В потоке жидкости выделим цилиндрический объем радиусом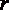 
, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, которое представляет собой равенство нулю суммы сил давления и сопротивления, действующих на объем,
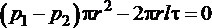
откуда
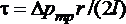, (1.6.1)
где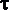 
- касательное напряжение на боковой поверхности выделенного цилиндра.
Из формулы (1.6.1) следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в зависимости от радиуса. На оси трубы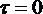 
, так как 
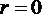. На стенке трубы, где 
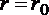, касательные напряжения достигают максимального значения.
|
|
|
Эпюра касательного напряжения показана на рис. 1.6.2 слева.
Касательное напряжение 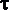по закону трения Ньютона можно выразить через динамическую вязкость и поперечный градиент скорости (1.1.12), а если при этом заменить 
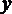(расстояние от стенки трубы) текущим радиусом, то получим
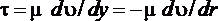. (1.6.2)
Знак минус обусловлен тем, что направление отсчета 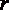(от оси трубы к стенке) противоположно направленно отсчета 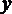(от стенки).
Приравняв правые части уравнений (1.6.1) и (1.6.2), получим
,
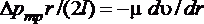откуда приращение скорости
. (1.6.3)
При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рис. 1.6.2.
Выполнив интегрирование выражения (1.6.3) для условия, что на стенке трубы при 
, получим закон распределения скоростей по сечению круглой трубы при ламинарном движении жидкости
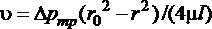. (1.6.4)
Максимальная скорость на оси трубы (при условии, что )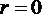
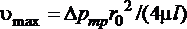, (1.6.5)
а кривая, изображающая эпюру скорости (рис. 1.6.2 справа), является параболой второй степени.
Элементарный расход 
жидкости через бесконечно малую площадку 
|
|
|
.
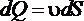Если 
представить в виде функции радиуса 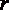(1.6.4), а площадку - в виде кольца радиусом 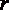и шириной 
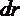, то
.
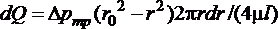После интегрирования по всей площади поперечного сечения, то есть от 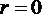до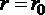 
, получим
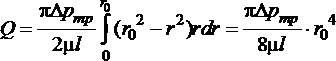. (1.6.6)
Среднюю по сечению скорость жидкости найдем делением расхода на площадь. С учетом выражения (1.6.6) получим
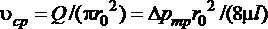. (1.6.7)
Сравнение полученного выражения с формулой (1.6.5) показывает, что средняя скорость при ламинарном движении в два раза меньше максимальной: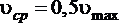 
.
Из этого следует, что коэффициент Кориолиса , учитывающий неравномерность распределения скоростей по сечению в уравнении Бернулли (1.4.9),для случая установившегося ламинарного движения жидкости в круглой трубе, равен двум.
Следовательно, действительная кинетическая энергия ламинарного потока с параболическим распределением скоростей по сечению в два раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.
Дата добавления: 2018-08-06; просмотров: 1035; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!