Сила давления жидкости на наклонные жидкости. Центр давления
В практике часто встречаются плоские поверхности (щиты, стенки), расположенные под каким-либо углом 
к горизонту.
Выведем расчётную зависимость для определения силы давления жидкости на наклонную плоскую стенку (рис.2.18).
Рис. 2.18
Для этого:
1) выделим элементарную площадку 
, расположенную на глубине h;
2) выберем оси координат, развернём их на прямой угол;
3) обозначим центр тяжести щита (Ц.Т).
На будет действовать элементарная сила гидростатического давления
, (2.80)
где 
– плотность жидкости, кг/м3; 
– избыточное гидростатическое давление, Па; 
– давление на свободной поверхности жидкости, Па.
Суммарная сила гидростатического давления на весь щит равна сумме элементарных сил, действующих по всей смоченной площади щита. Проинтегрируем выражение (2.80) по площади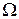 
. (2.81)
Из рис.2.18 видно, что 
, тогда
, (2.82)
где 
– статический момент площади относительно оси ОХ, он равен произведению площади на расстояние от Ц.Т. до оси ОХ, значит
. (2.83)
Из рис.2.18 видно, что 
. Тогда, с учётом этого, подставив (2.83) в (2.82), получим
. (2.84)
Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления.
Внешняя сила 
приложена в Ц.Т площади, сила избыточного давления приложена ниже Ц.Т, в – Ц.Д (центре давления).
В случае, если 
(рис. 2.19), на щит будет действовать с одной стороны атмосферное давление, а с другой – давление со стороны жидкости, направленные навстречу друг к другу, то формула (2.84) примет вид
|
|
|
. (2.85)
Точка приложения результирующей силы давления жидкости на любую поверхность называется центром давления.
Применительно к рис. 2.12 центром давления является т. D. Определим координаты центра давления (xD; zD) для любой плоской поверхности.
Из теоретической механики известно, что момент равнодействующей силы относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси. За ось в нашем случае примем ось Ох (см. рис. 2.12), тогда
Известно также, что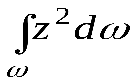 
является моментом инерции площади 
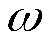относительно оси Ox 
В результате получаем
откуда
Подставим в это выражение формулу (2.9) для F и геометрическое соотношение 
:
Перенесем ось момента инерции в центр тяжести площадки 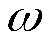. Обозначим момент инерции относительно оси, параллельной оси Ох и проходящей через т.С, через 
. Моменты инерции относительно параллельных осей связаны соотношением
;
тогда 
и окончательно получим
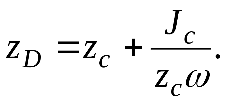(2.11)
Формула показывает, что центр давления расположен всегда ниже центра тяжести площадки, за исключением случая, если площадка горизонтальна и центр давления совпадает с центром тяжести. Для простых геометрических фигур моменты инерции относительно оси, проходящей через центр тяжести и параллельной оси Ох (рис. 2.12), определяются по следующим формулам:
|
|
|
для прямоугольника
(2.12)
где сторона основания параллельна Ох;
для равнобедренного треугольника
(2.13)
где сторона основания параллельна Ох;
для круга
(2.14)
Дата добавления: 2018-08-06; просмотров: 389; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!