Дифференциальные уравнения с разделяющимися переменными.
, 
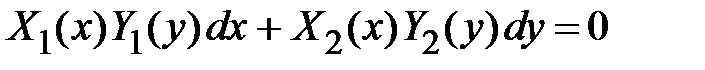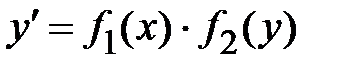(общий вид),
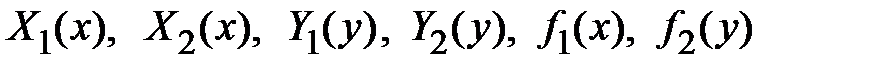- непрерывные функции.
Нахождения общего решения: x и y разделяют, чтобы в каждом слагаемом уравнения содержались только x и dx, или y и dy, dx и dy – все в числителях. Разделяем переменные: ,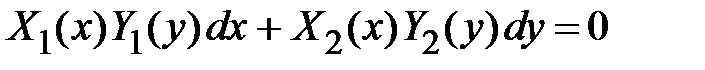 
, 
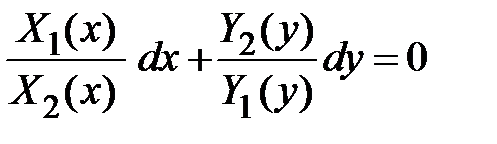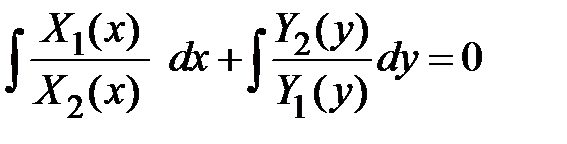. Если 
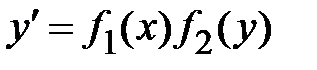, то 
.
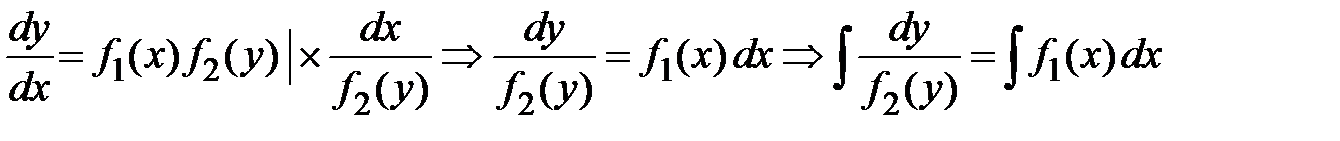3. Третий признак сравнения знакоположительных рядов. Т.1. Если отношение последующего члена ряда к предыдущему для ряда 
не превосходит соответствующего отношения последующего члена ряда к предыдущему для сходящегося ряда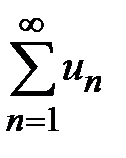 
, т. е. 
для любого n, то ряд сходится. 2. Если же 
и ряд расходится, то и ряд 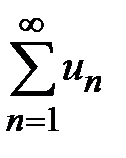расходится. Док: для любого n: 
, 
, 
, если 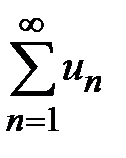сходится, сходится, так как 
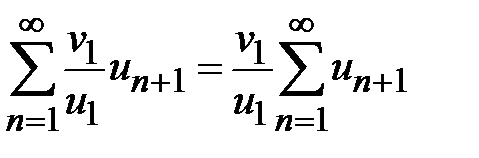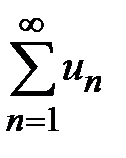. Если расходится, то расходится.
Билет 20.
1. Метод множителей Лагранжа.Левые части уравнения – частые производные ф-ции: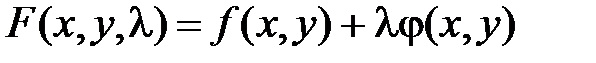 
(ф-ция Лагранжа). Система для нахождения крит.т.:
, 
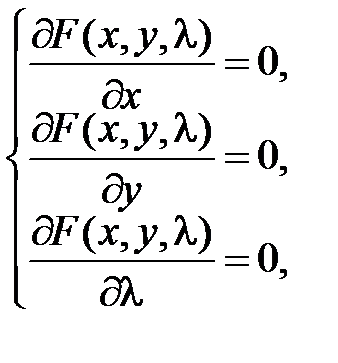(в случае n переменных):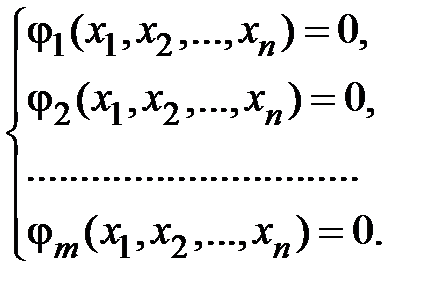 
Ф-ция Лагранжа: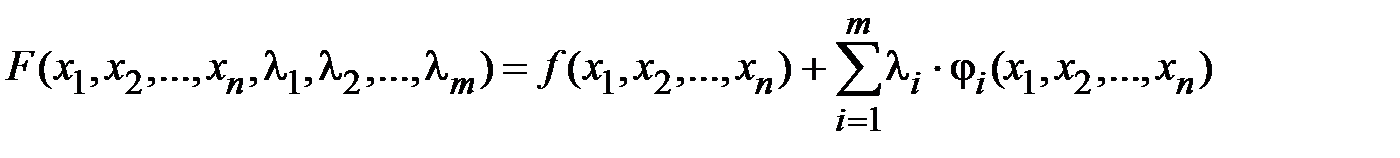 
.
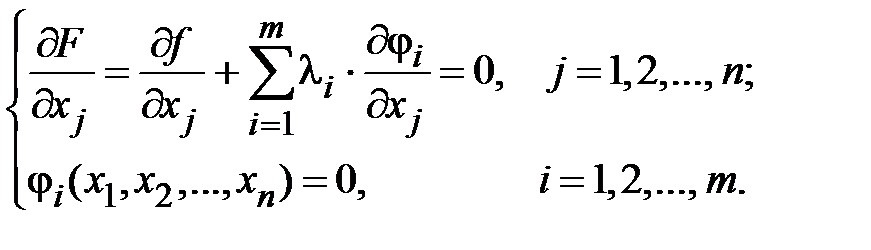,крит. Т.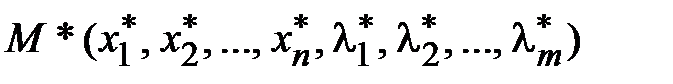 
Достаточный признак условного экстремума.Пусть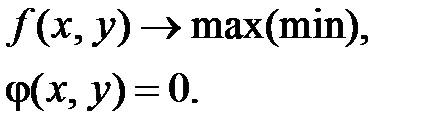 
, ф-ция Лагранжа: 
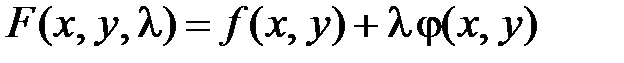. Сис-ма для кр. Т.: 
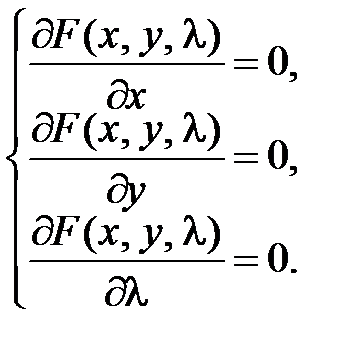, найдена критическая точка 
, 
, 
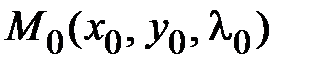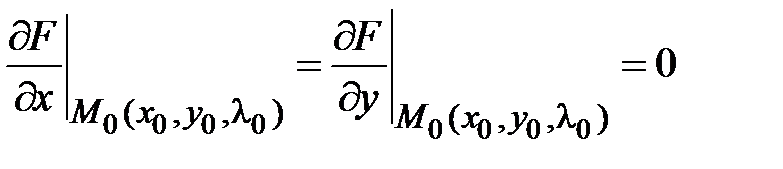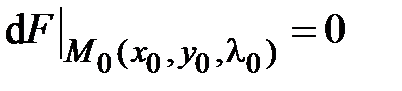. Наличие экстремума в точке: является ли знакоопределенной функцией приращение функции 
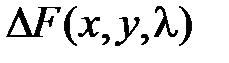в этой точке. Если 
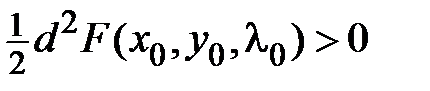, то 
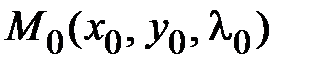, - точка минимума. Если 
, 
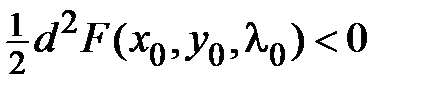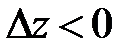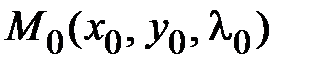, - точка максимума.
Дифференциал второго порядка: 
, 
, 
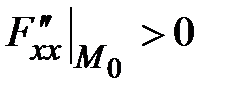. Минимум – в т. 
. 
. 
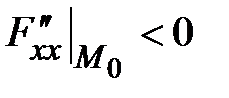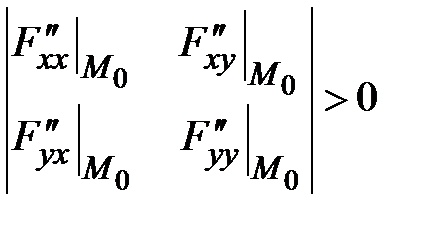, максимум - в точке .
2. Комплексные числа и действия над ними.Комплексным числом называется выражение вида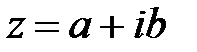 
, где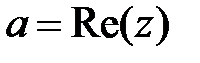 
- реальная часть z (действительное число), 
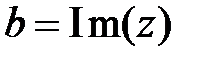- мнимая часть z, 
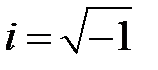- мнимая единица. 
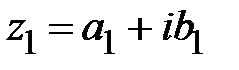и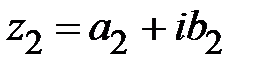 
равны, если 
, 
. Комплексное число равно нулю, если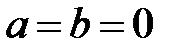 
. Угол 
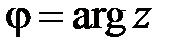называется аргументом комплексного числа. В тригонометрическом виде 
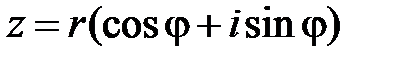. Действия над комплексными числами.1. Сложение (вычитание) комплексных чисел. 
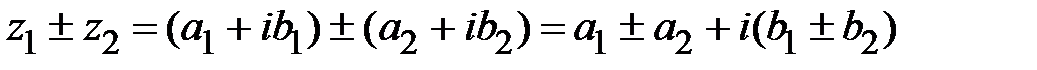. 2.Умножение комплексных чисел. 
, 
, 
, 
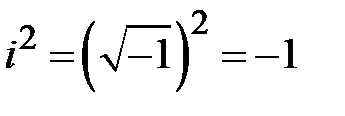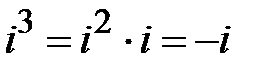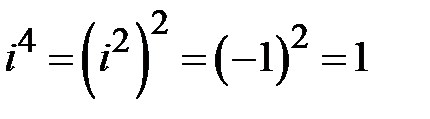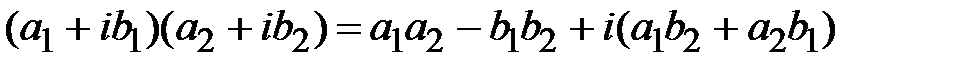. 3. Возведение в степень комплексного числа, 
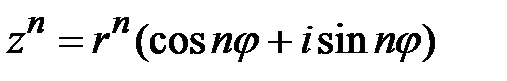. 4. Деление комплексных чисел. 
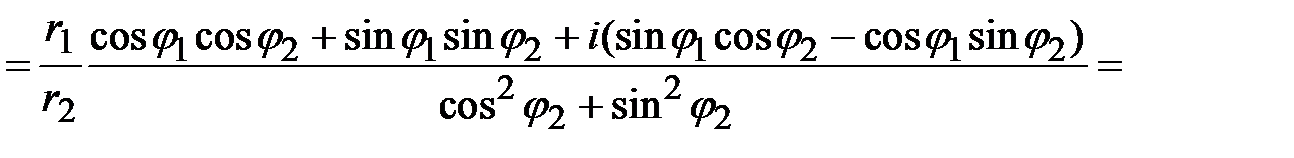5. Извлечение корня из комплексного числа.
|
|
|
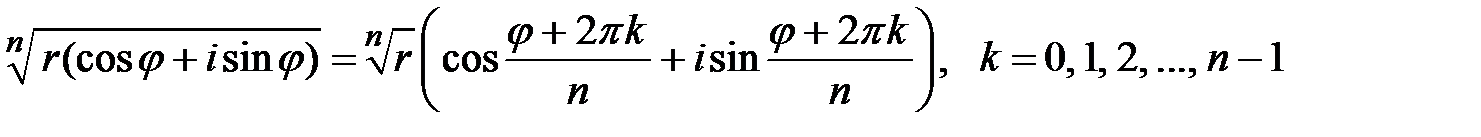. Формула Эйлера. 
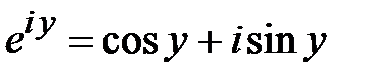. Комплексное число в показательной форме: 
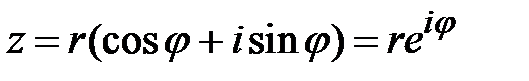, r – модуль комплексного числа, а j- его аргумент.
, 
.
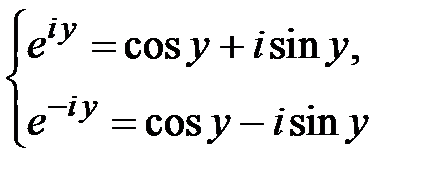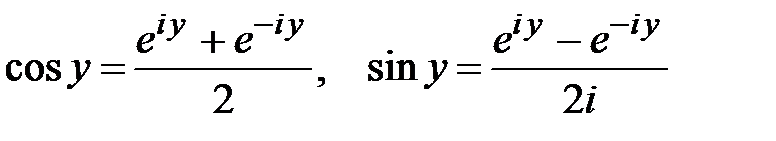3. Необходимые и достаточные условия разложения функции в степенной ряд. Ряды Тейлора и Маклорена. Функция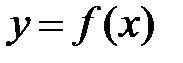 
разлагается в степенной ряд 
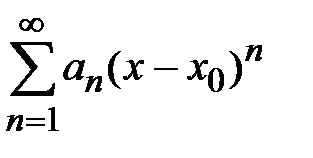в области G, если он составлен для этой функции и сходится к ней.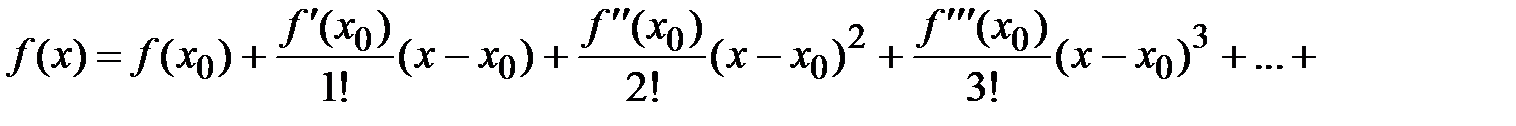 
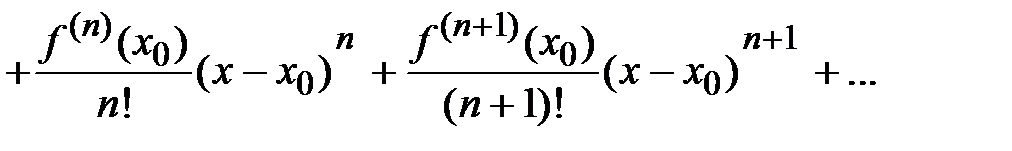- ряд Тейлора. Если 
: 
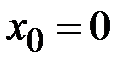- ряд Маклорена. Разложения функций по данным формулам справедливы только в области сходимости этих рядов. Т. Для того чтобы степенной ряд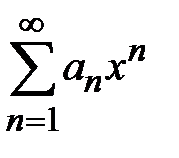 
сходился к функции 
, для которой он составлен, необходимо и достаточно, чтобы остаточный член ряда стремился к нулю при неограниченном увеличении его номера n, т. е.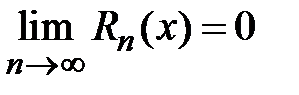 
. Док: Необходимость. 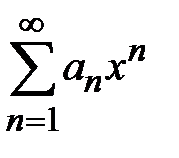сходится к , 
, 
, 
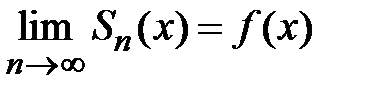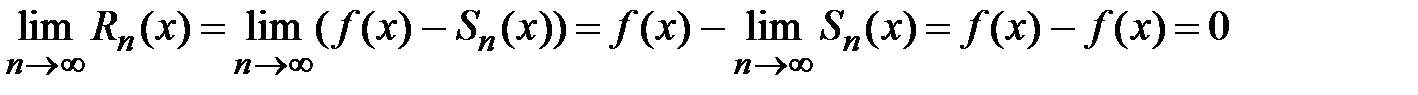. Достаточность. . 
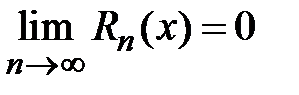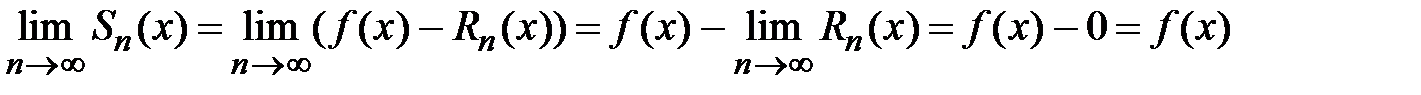, сходится.
|
|
|
Дата добавления: 2018-08-06; просмотров: 219; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!