Применение полного дифференциала функции нескольких переменных для приближенных вычислений
1. Вычисление значений функций и их приращений.Используем то, что полный дифференциал является главной линейной частью приращения функции (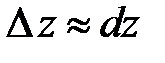 
). Пусть известно значение функции 
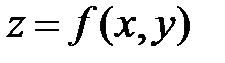в некоторой точке 
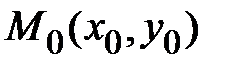и имеется точка 
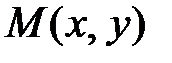, находящейся в некоторой достаточно малой окрестности точки 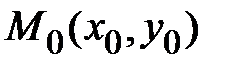. Можно найти приращение функции 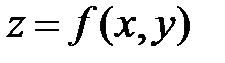по формуле 
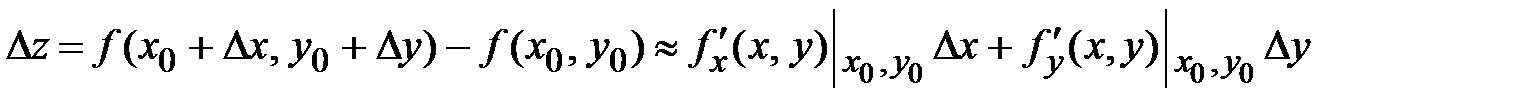.Можно найти также значение этой функции в точке 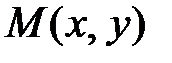по формуле
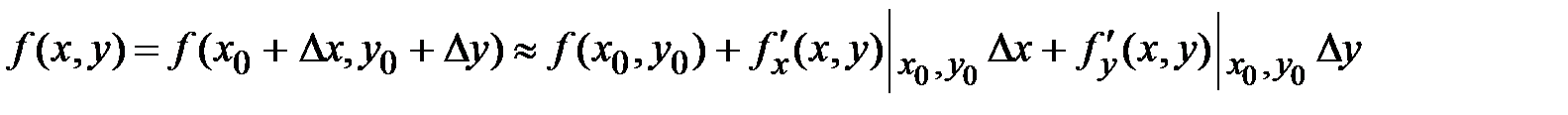.Здесь 
, 
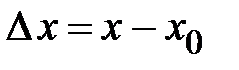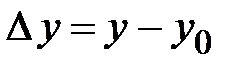- приращения независимых переменных,
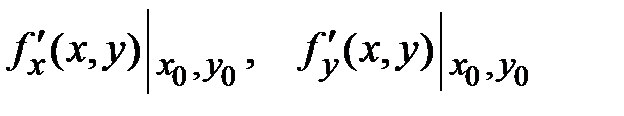- значения частных производных функции в точке .
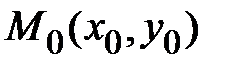Методы интегрирования определенных интегралов
При вычислении определенных интегралов используются те же методы, что и при нахождении неопределенных интегралов. Однако, имеются некоторые особенности.1. Замена переменной в определенном интеграле отличается от замены переменной в неопределенном интеграле тем, что в результате замены изменяются пределы интегрирования и нет необходимости выполнять обратную замену. Пусть функция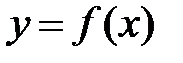 
непрерывна на отрезке 
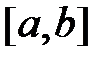, функция 
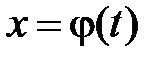имеет непрерывную производную на отрезке 
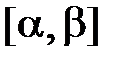. Тогда 
.
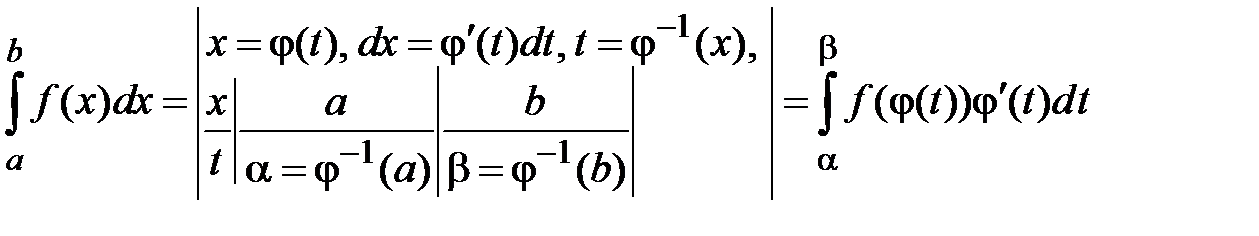Пример 5.2.Найти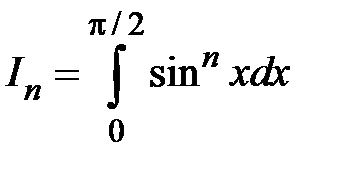 
, где 
.
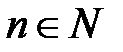Используем интегрирование по частям для нахождения рекуррентной формулы для вычисления интегралов вида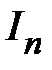 
при любом nÎN.
.
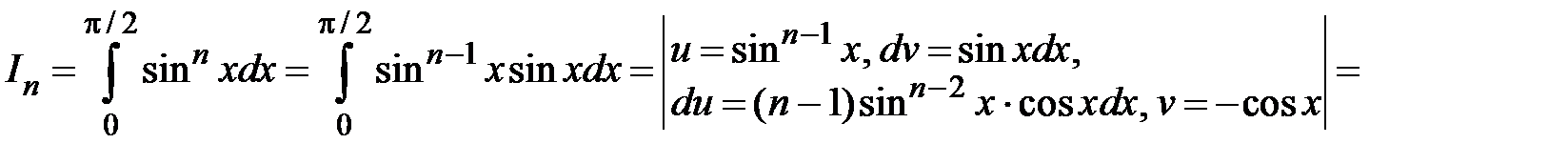
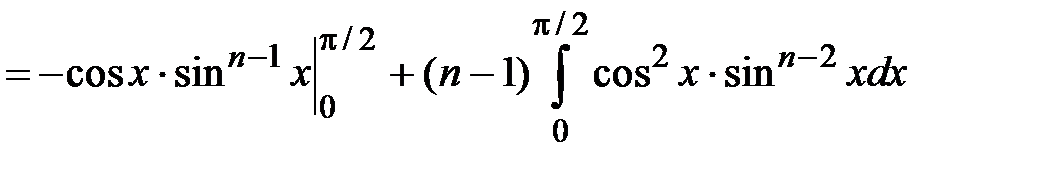Учтем, что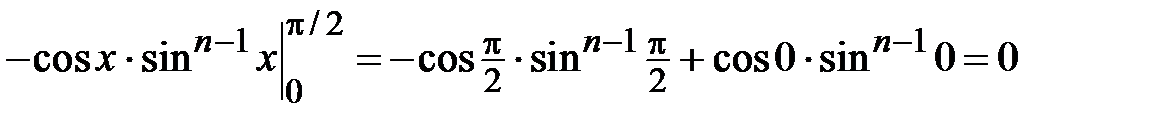 
, получим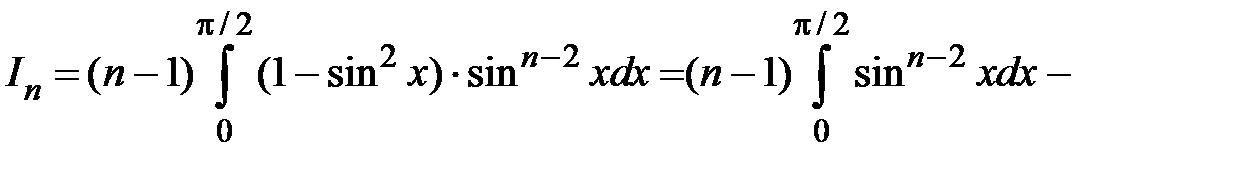 
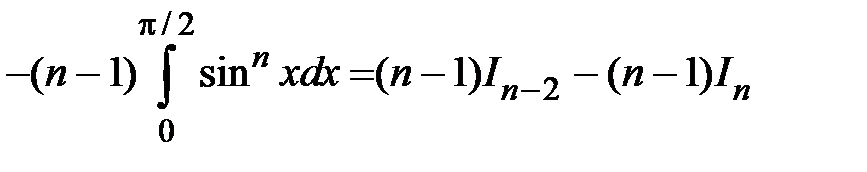.Получили уравнение относительно интеграла 
: 
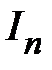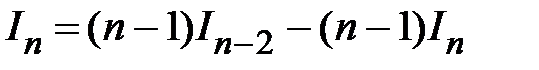. Отсюда получаем рекуррентную формулу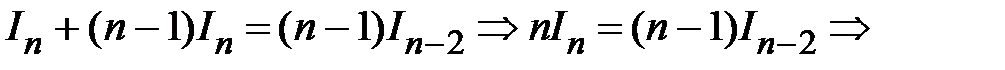 
.
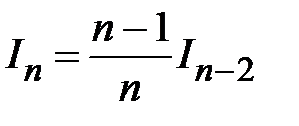Знакопеременные ряды. Теорема об абсолютной сходимости
|
|
|
Числового ряда
Теорема 8.8.Числовой ряд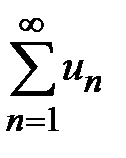 
сходится, если сходится ряд, составленный из абсолютных величин его членов 
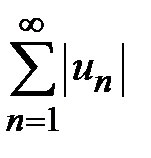.Д о к а з а т е л ь с т в о. Пусть ряд 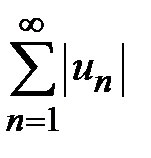сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд 
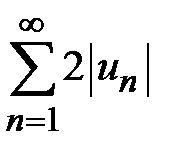. Так как 
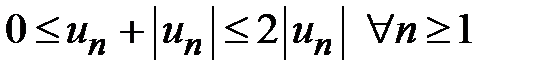, то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд 
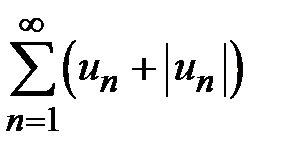. На основании свойства 2 сходящихся рядов сходится разность двух рядов 
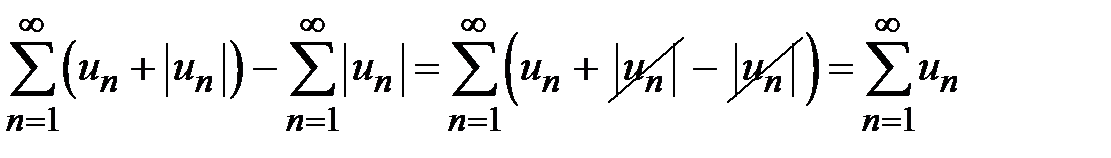, т. е. исходный ряд. Ряд называется абсолютно сходящимся, если он сходится и сходится ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Билет 15.
1. Метод наименьших квадратов.При решении экономических задач часто возникает необходимость представления опытных данных в аналитическом виде. Наиболее известным математическим методом для этих целей является метод наименьших квадратов.Пусть имеются опытные данные в виде таблицы
|    . . . . . . . 
|
|    . . . . . . . 
|
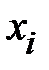
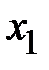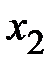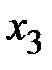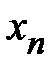
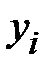
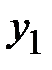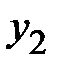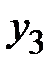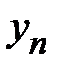
из двух строк, в первой строке которой находятся значения некоторой переменной, принимаемой за независимую, а во второй соответствующие значения другой переменной, принимаемой за функцию. Требуется найти аналитическую функциональную зависимость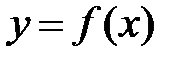 
. Наиболее просто найти аналитическую зависимость возможно с помощью интерполяционного многочлена Лагранжа, который в общем виде записывается следующим образом 
.
|
|
|
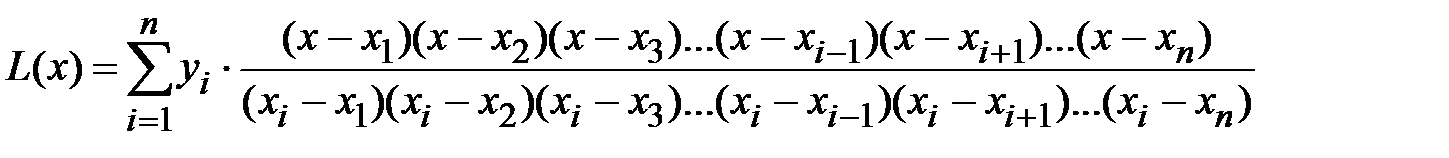График данной функции проходит совершенно точно через заданные точки (рис.)
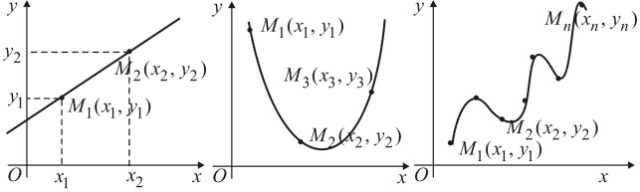
В случае, если имеются два точки 
, 
, то данная формула позволяет написать уравнение прямой, проходящей через эти точки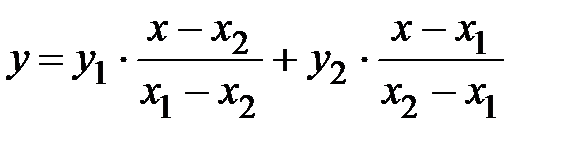 
. В случае, если имеются три точки , , 
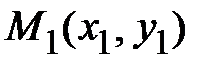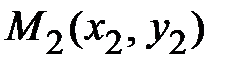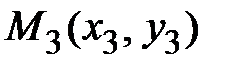, то данная формула позволяет написать уравнение параболы, проходящей через эти точки 
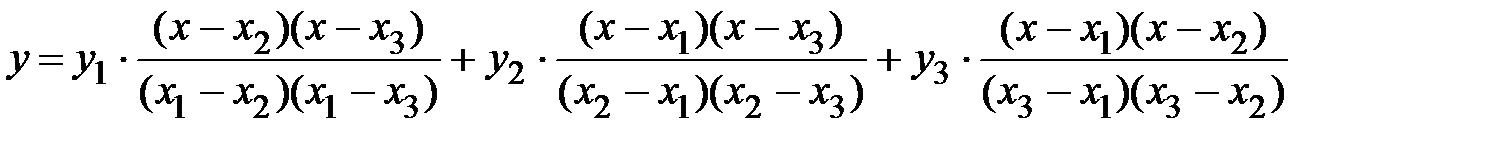. Если известно n точек, то можно написать уравнение линии, представляющей многочлен (n-1)-ой степени относительно х.
2. Дифференциальные уравнения с разделяющимися переменными. Данные уравнения являются наиболее простыми из дифференциальных уравнений. Однако решение многих типов дифференциальных уравнений сводится к решению дифференциальных уравнений с разделяющимися переменными. В общем случае данные уравнения можно записать в виде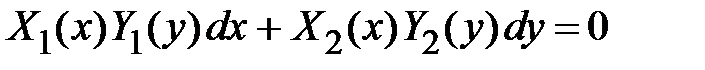 
или 
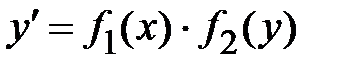, где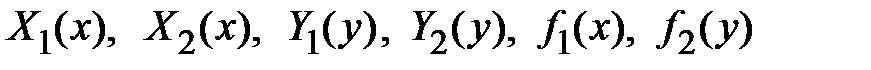 
- непрерывные функции. Для нахождения общего решения уравнения переменные x и y в уравнении с помощью алгебраических действий разделяют так, чтобы в каждом слагаемом уравнения содержалась только одна переменная и ее дифференциал, либо x и dx, либо y и dy. Дифференциалы dx и dy. должны быть всегда в числителях дробей. Разделяем переменные. Уравнение вида 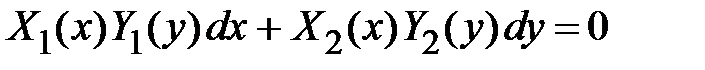делим на 
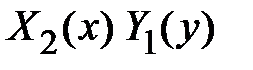, получаем 
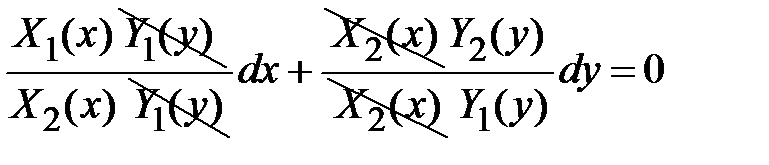Þ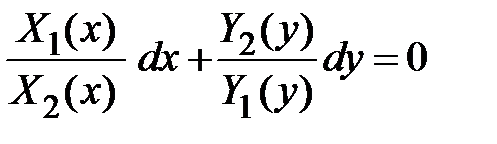 
. После того, как переменные разделены, решение уравнения сводится к интегрированию. Записываем 
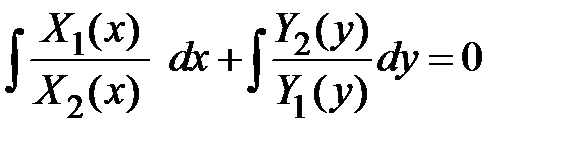.Таким образом, решение дифференциального уравнения сводится к нахождению интегралов. Если уравнение имеет вид 
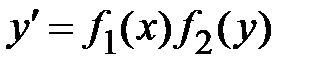, то переменные разделяем следующим образом 
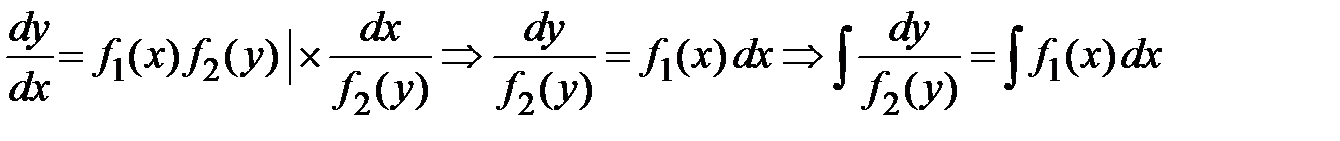. Если решение дифференциального уравнения сведено к нахождению интегралов, то считается, что оно в принципе решено. Поэтому часто говорят не решить, а проинтегрировать дифференциальное уравнение. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями).Функция 
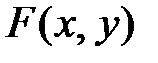называется однородной n-го измерения, если 
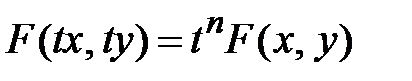, где t – параметр. Например, для функции 
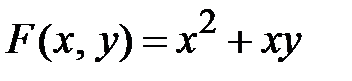находим 
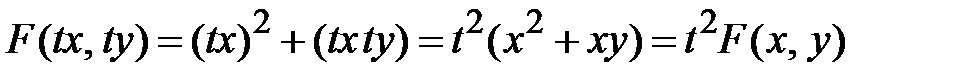. Следовательно, эта функция второго измерения (n = 2). Покажем, что частное двух однородных функци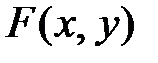й 
и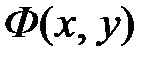 
одного и тоже измерения есть однородная функция нулевого измерения. Действительно, 
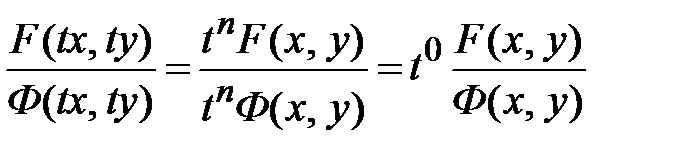. Однородными дифференциальными уравнениями называются уравнения вида 
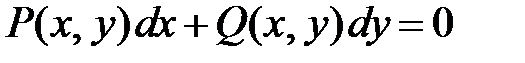, где 
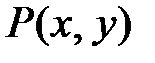и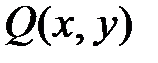 
- однородные функции одного измерения.
|
|
|
Данное уравнение можно привести к уравнению с разделяющимися переменными. Для этого преобразуем уравнение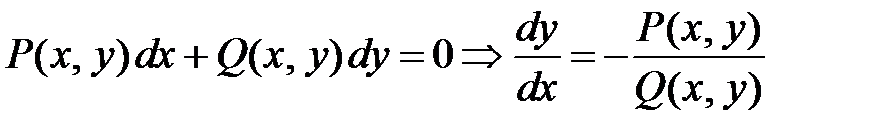 
. Обозначим 
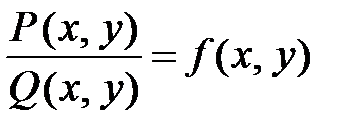. Тогда уравнение примет имеет вид 
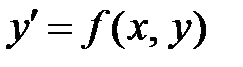, где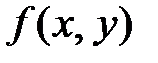 
- однородная функция нулевого измерения, т. е. 
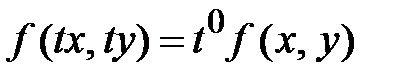. Если принять параметр 
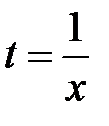, то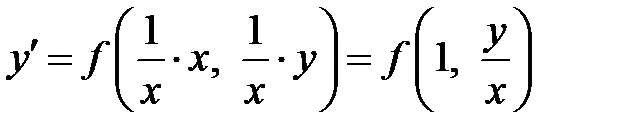 
. Уравнение 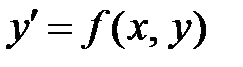сводится к уравнению с разделяющимися переменными с помощью подстановки 
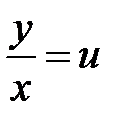или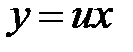 
, где u = u (x)- функция от x. Найдем производную 
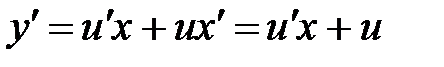и подставим ее в уравнение, получим 
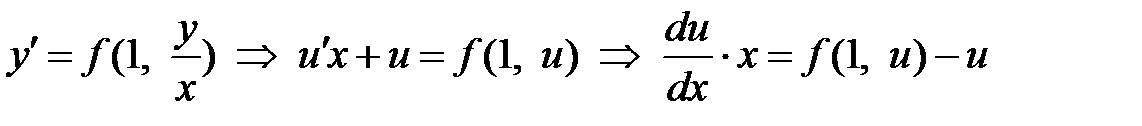. Разделим переменные и проинтегрируем
|
|
|
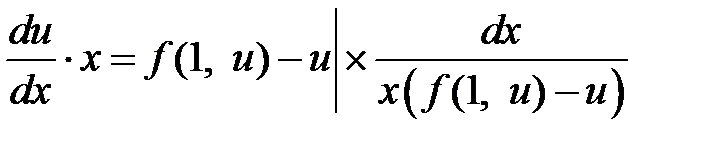Þ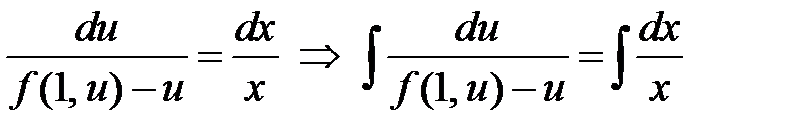 
. Решение уравнения сведено к нахождению интегралов. В результате интегрирования будет получен общий интеграл 
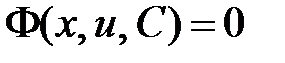. Для нахождения общего интеграла исходного дифференциального уравнения необходимо сделать обратную замену переменной 
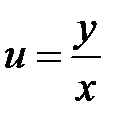, в результате которой общий интеграл будет иметь вид 
.
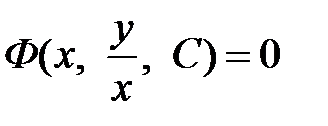3.Первый признак сравнения рядов.1. Если члены знакоположительного ряда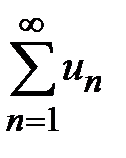 
не превосходят соответствующих членов сходящегося ряда 
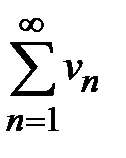, т. е. 
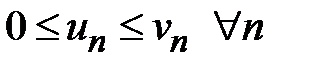, то он сходится. 2. Если члены знакоположительного ряда 
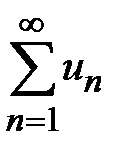не меньше соответствующих членов расходящегося ряда 
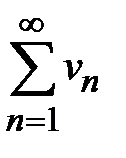, т. е. 
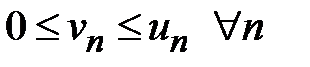, то он расходится. Д о к а з а т е л ь с т в о. Докажем первое утверждение теоремы. Пусть ряд 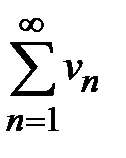сходится и его сумма равна 
.
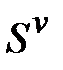Ряд 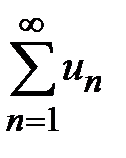знакоположительный, поэтому последовательность его n-ых частичных сумм 
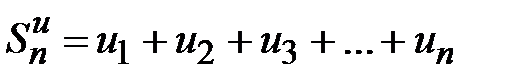монотонно возрастает при увеличении n. Члены ряда 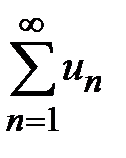не превосходят соответствующих членов ряда 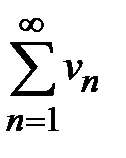, т. е. 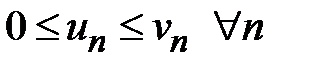. Ввиду этого частичные суммы рядов удовлетворяют неравенству 
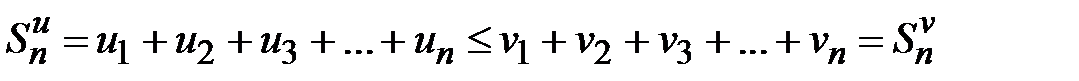.Кроме того, очевидно, что 
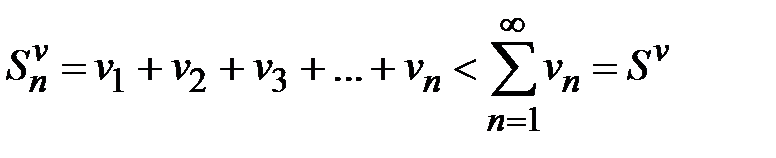. Следовательно, последовательность частичных сумм 
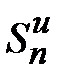монотонно возрастает и ограничена ( 
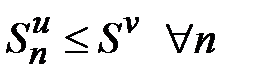). По теореме Вейерштрасса эта последовательность имеет предел 
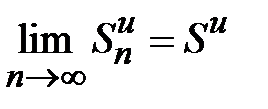. Ряд 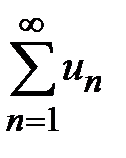сходится. Второе утверждение теоремы докажем от противного. Пусть известно, что ряд 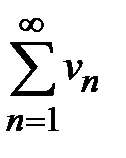расходится и 
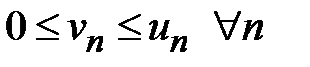. Предположим, что ряд 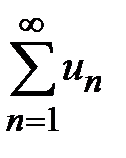сходится. Тогда по первому утверждению данной теоремы должен сходиться также ряд 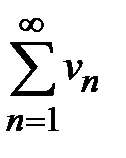. В этом и состоит противоречие.
Билет 16.
Дата добавления: 2018-08-06; просмотров: 478; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!