Производная функции по направлению
Пусть функция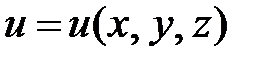 
непрерывная и дифференцируемая, вектор 
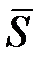задает направление. Пусть имеется точка 
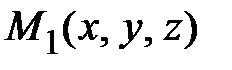и в направлении 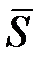от нее точка 
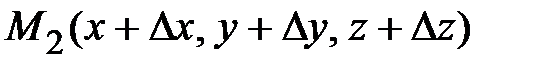рис. Вектор 
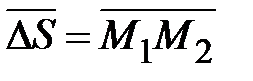имеет координаты 
, 
, 
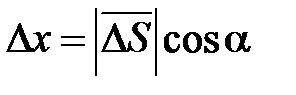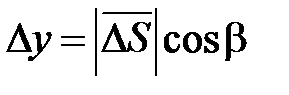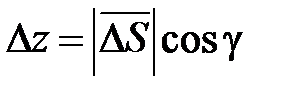, т. е. 
.
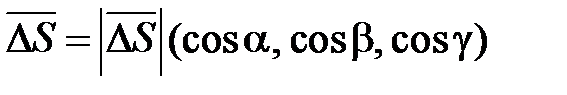Модуль вектора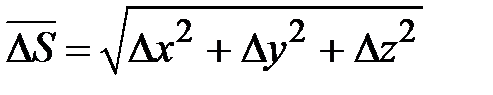 
, 
, 
, 
.
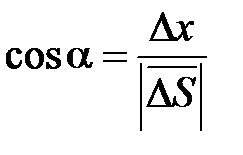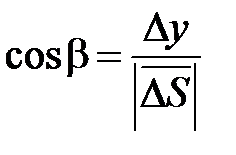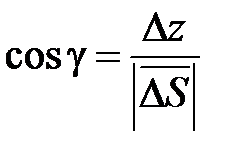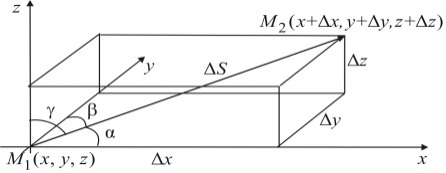Косинусы cosa, cosb, cosg называются направляющими косинусами вектора 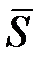. Если вектор 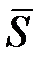единичный 
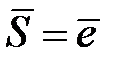, то 
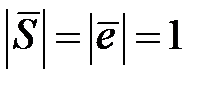и его координатами являются направляющие косинусы, т. е. 
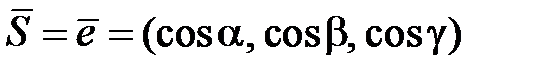. Производной функции 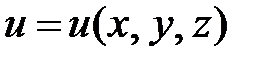по направлению вектора 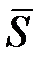в точке 
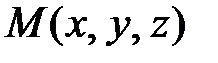называется предел отношения приращения функции в этом направлении к приращению длины (модуля) 
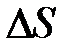вектора 
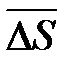, при 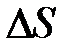стремящемся к нулю 
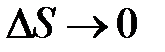, т. е. 
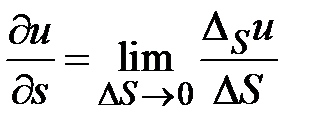. Находим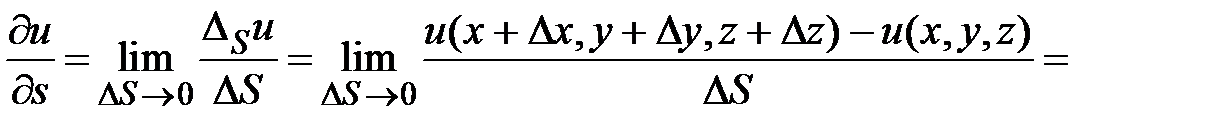 
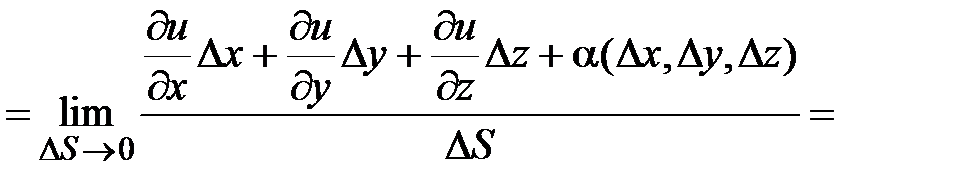
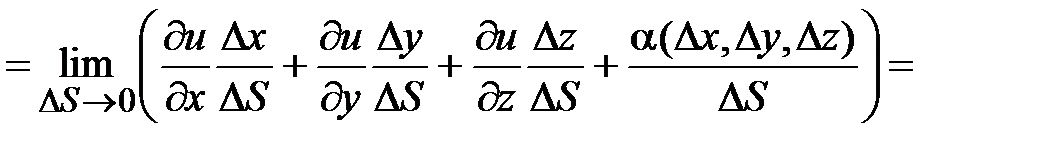
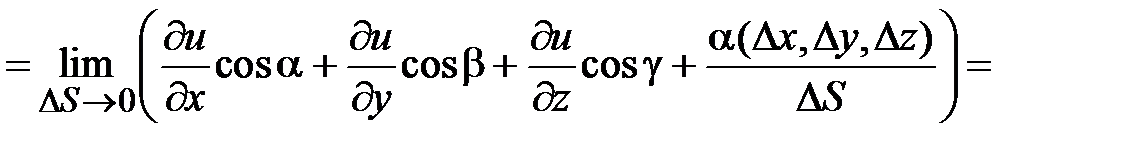
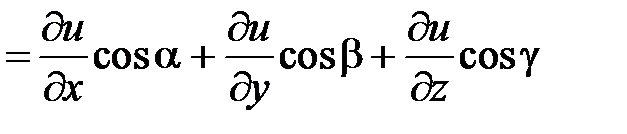. Таким образом, получена формула дифференцирования функции по направлению вектора 
.
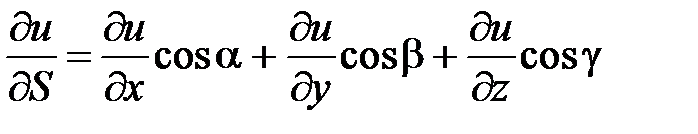Градиент функции, его свойства
Градиентом функции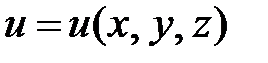 
называется вектор 
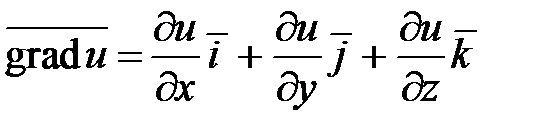, где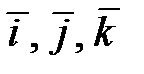 
- единичные векторы координатного базиса в прямоугольной декартовой системе координат. Кратко можно записать 
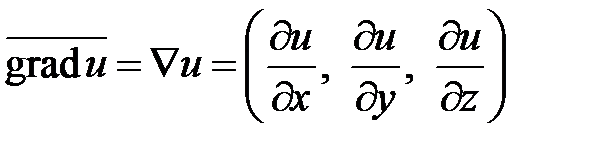. Здесь Ñ- знак набла. Теорема 3.5. Производная функции 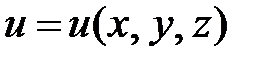по направлению вектора 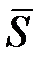равняется проекции градиента этой функции на это направление, т. е. 
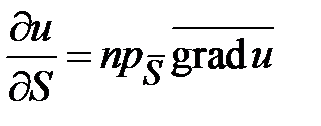. Известно, что проекция некоторого вектора 
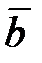на направление вектора 
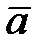равняется 
.
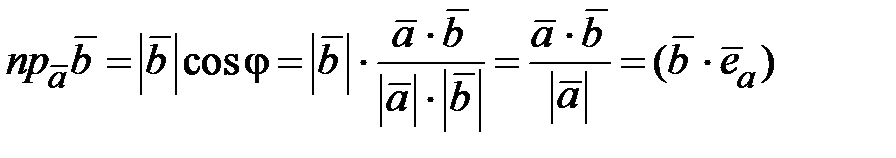Здесь j- угол между векторам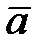и и ,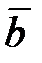 
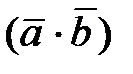- скалярное произведение векторов, 
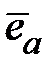- единичный вектор, совпадающий по направлению с вектором 
.
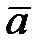Найдем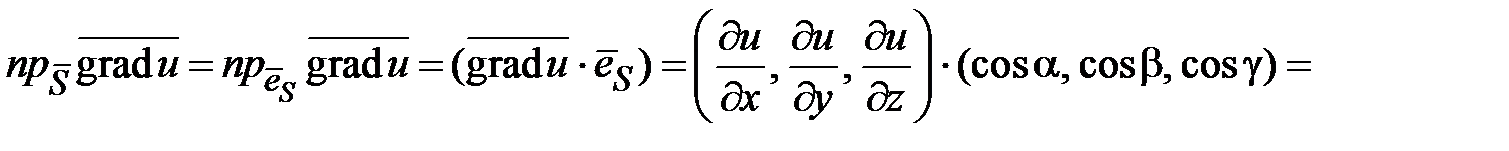 
.
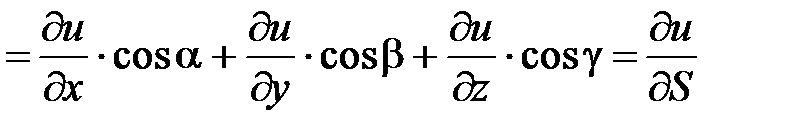
Свойство 1. Производная функции 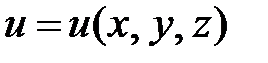по направлению вектора 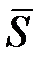достигает своего наибольшего значения, если направление вектора 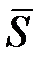совпадает с направлением градиента этой функции. Действительно, производную данной функции по направлению вектора 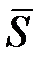можно записать следующим образом 
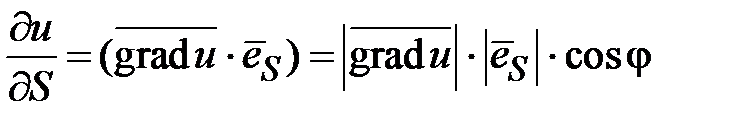, где j- угол между градиентом и вектором 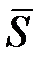. Если этот угол равен нулю j = 0 , то косинус этого угла и производная функции принимают наибольшие значения, cos0 = 1, 
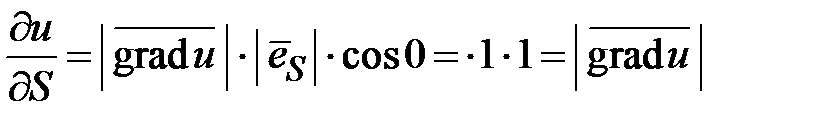. Свойство 2. Производная функции 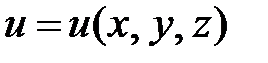по направлению вектора 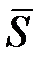равняется нулю, если направление вектора 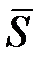перпендикулярно направлению градиента этой функции. Действительно, 
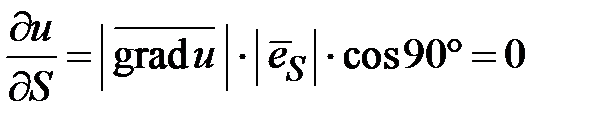. Данные свойства используются при решении задач оптимизации (нахождения наибольшего, наименьшего значений функций) с помощью численных методов. Градиент функции определяет направление наибольшего изменения функции. Направление перпендикулярное градиенту определяет направление, в котором функция не изменяется. Известно, что на поверхности уровня 
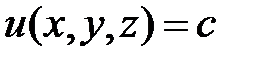функция 
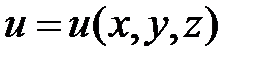не изменяется. Следовательно, градиент функции перпендикулярен поверхности уровня. Это обстоятельство можно использовать для написания уравнения касательной плоскости к поверхности 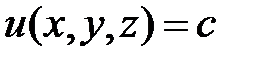. Пусть точка 
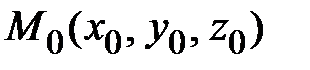принадлежит поверхности. Найдем градиент функции 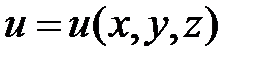в этой точке 
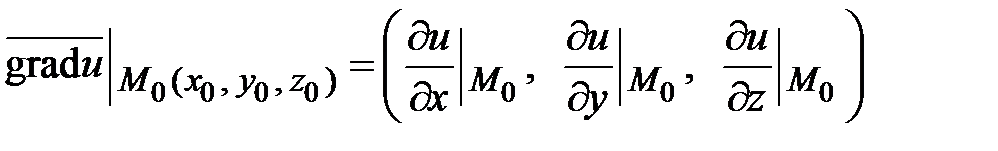и напишем уравнение плоскости, проходящей через точку 
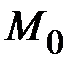перпендикулярно вектору 
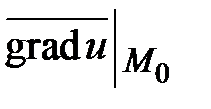. Получаем уравнение касательной плоскости 
.
|
|
|
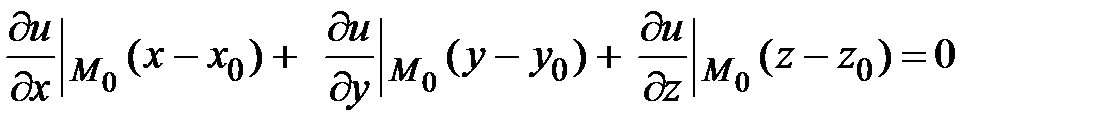2. Общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.Общее решение неоднородного уравнения, как было показано ранее (теорема 7.4), находится как сумма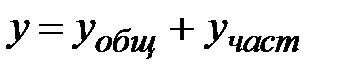 
общего решения 
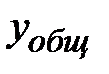однородного уравнения и частного решения 
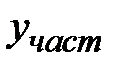неоднородного уравнения, т. е. 
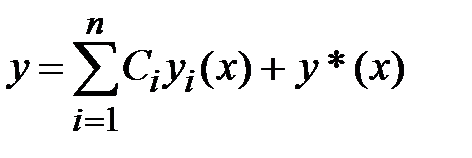, где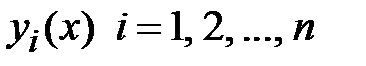 
- линейно независимые решения однородного уравнения;
|
|
|
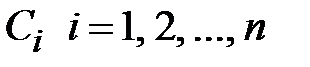-произвольные постоянные; 
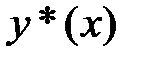- частное решение исходного неоднородного уравнения. В общем случае линейное однородное дифференциальное уравнение n-го порядка имеет вид 
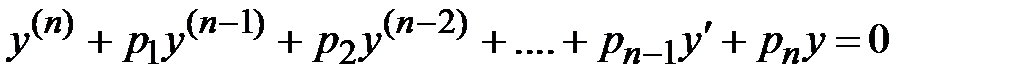, где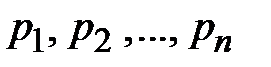 
- постоянные величины. Частные решения однородного уравнения ищут в виде 
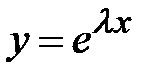. Производные этой функции равны 
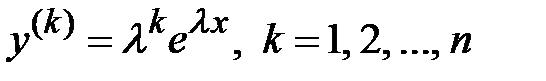. Подставляем функцию 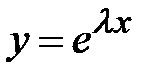и ее производные в однородное уравнение 
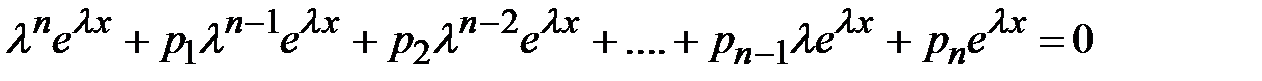. Делим это уравнение на 
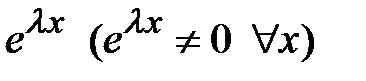, получаем уравнение 
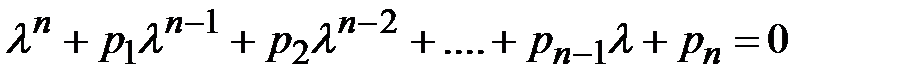. Данное уравнение называется характеристическим. Характеристическое уравнение является алгебраическим уравнением n-ой степени относительно l. Любое алгебраическое уравнение n-ой степени имеет в комплексной плоскости n корней. Рассмотрим все возможные случаи решения однородного дифференциального уравнения в зависимости от вида корней его характеристического уравнения. Случай 1. Все корни характеристического уравнения 
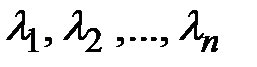вещественные различные. В этом случае дифференциальное уравнение имеет n линейно независимых частных решений 
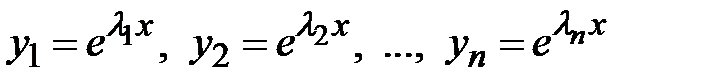. Общее решение однородного уравнения имеет вид 
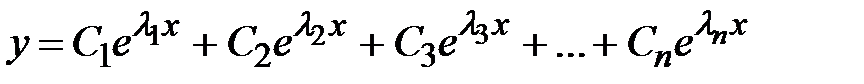или 
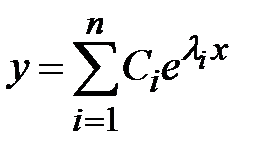, где 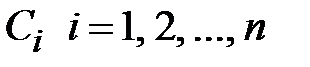- произвольные постоянные.Случай 2. Характеристическое уравнение имеет пару комплексно-сопряженных корней 
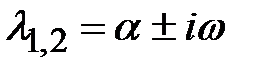, где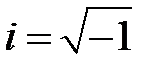 
. Тогда этим корням соответствует два линейно независимых комплексно-сопряженных решения 
, 
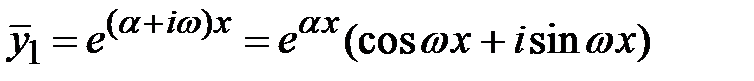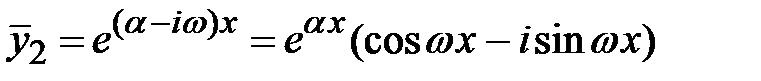. Из этих решений составляют два линейно независимых действительных решения 
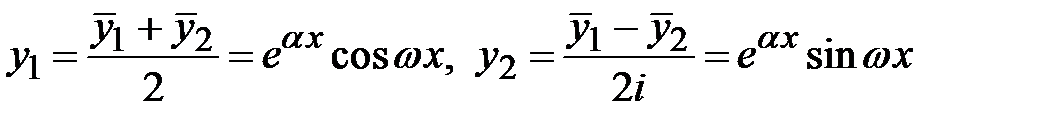. Общее решение однородного дифференциального уравнения имеет вид 
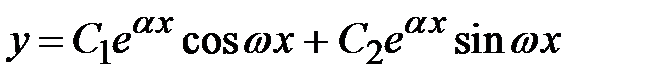или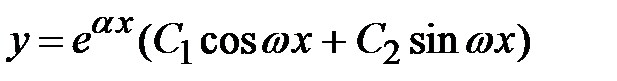 
. Случай 3. Характеристическое уравнение имеет действительный корень l кратности k. Тогда ему соответствуетk линейно независимых частных решения однородного уравнения, которые имеют вид 
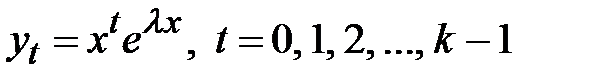. Общее решение однородного дифференциального уравнения имеет вид 
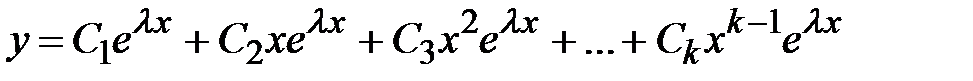. Случай 4. Характеристическое уравнение имеет пару комплексно-сопряженных корней 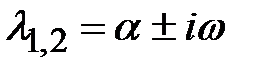кратности k. Тогда этим корням соответствует 2k линейно независимых частных решений однородного уравнения, которые имеют вид 
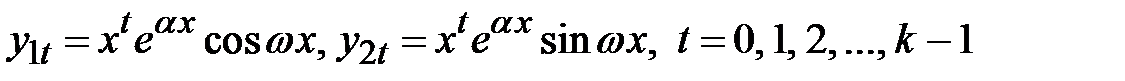. Общее решение однородного дифференциального уравнения имеет вид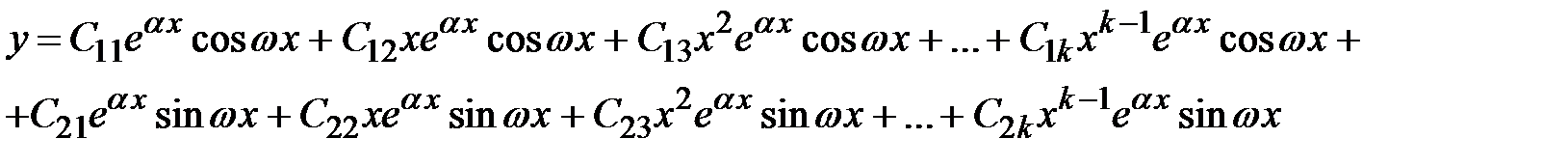 
|
|
|
Или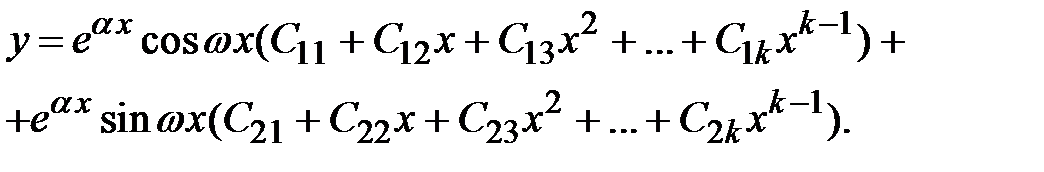 
3. Интегральный признак Коши.Если члены знакоположительного ряда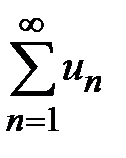 
, являющиеся значениями функции целочисленного аргумента 
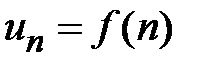, монотонно убывают и стремятся к нулю 
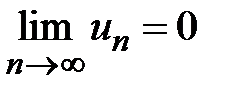, то: 1) если 
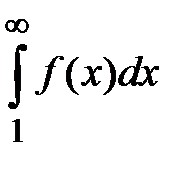сходится, то и ряд 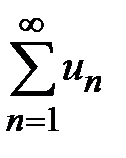сходится; 2) если 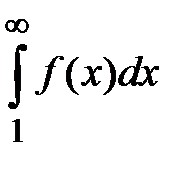расходится, то и ряд 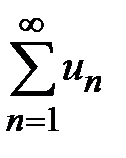расходится. Д о к о з а т е л ь с т в о. В прямоугольной декартовой системе координат 
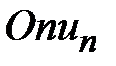непрерывная кривая 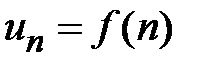проходит через точки 
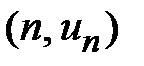и ограничивает сверху криволинейную трапецию ABCD (рис. 86). Площадь этой криволинейной трапеции равняется 
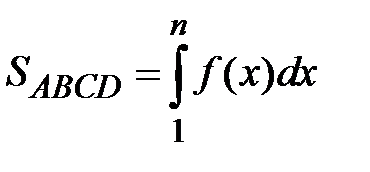. Построим две ступенчатые фигуры с угловыми точками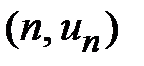 
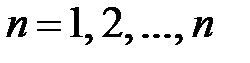. Эти ступенчатые фигуры состоят из прямоугольников, основания которых равняются единице, а высоты значениям 
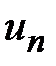. Найдем площади этих фигур. 
, 
,
|
|
|
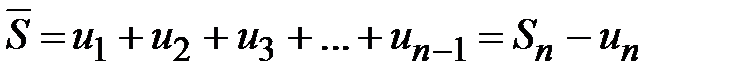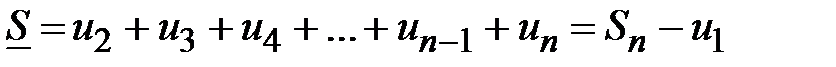где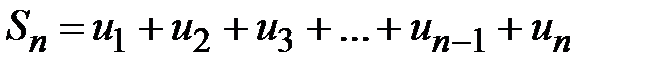 
-n-я частичная сумма ряда. Площади этих ступенчатых фигур ограничивают площадь криволинейной трапеции ABCD снизу и сверху 
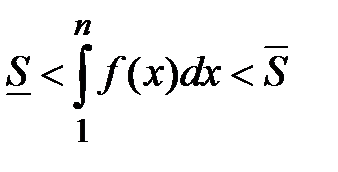Û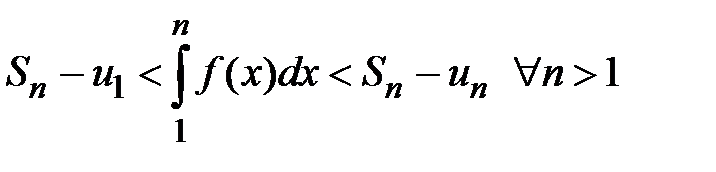 
.
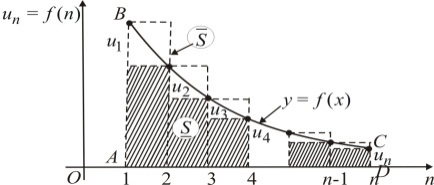Рассмотрим левую часть этого неравенства 
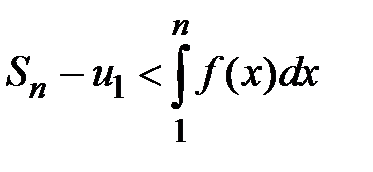Û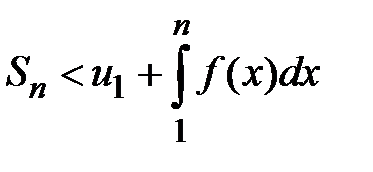 
.
При неограниченном возрастании числа n членов ряда частичные суммы ряда монотонно возрастают, так как ряд знакоположительный. При этом интеграл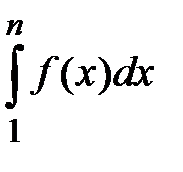 
также возрастает и ограничен величиной интеграла 
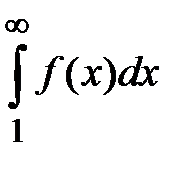. Поэтому 
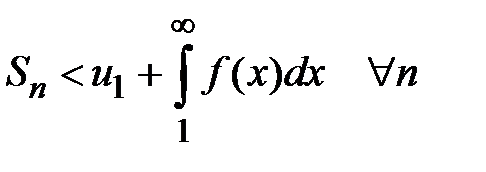, т. е. последовательность частичных сумм ограничена. По теореме Вейерштрасса существует предел 
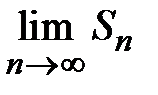. Следовательно, ряд сходится. Рассмотрим правую часть неравенства 
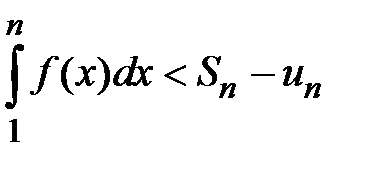Û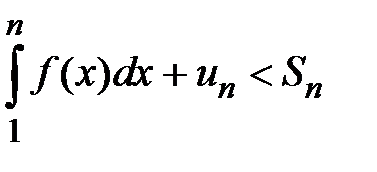 
. По условию теоремы 
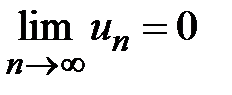. Если 
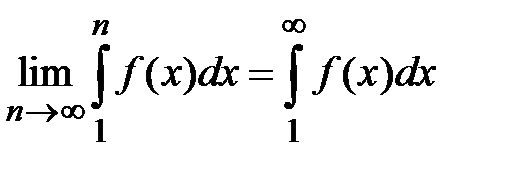неограниченно возрастает, то и предел частичных сумм 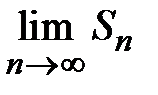неограниченно возрастает и, следовательно, ряд расходится. Таким образом, интегральный признак Коши в принципе позволяет для любого ряда решить вопрос о его сходимости. Трудность в его применении заключается в нахождении несобственных интегралов. Возможности в их нахождении ограниченные.
Билет 17.
1.Теорема Лагранжао конечном приращении функции. Если функция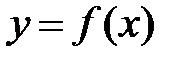 
непрерывна на отрезке 
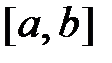и дифференцируемая в каждой его внутренней точке, то на интервале (a, b) найдется такая точка х = с, что 
.
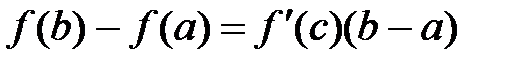Дата добавления: 2018-08-06; просмотров: 226; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!