Регрессионный метод и анализ ковариаций ANCOVA
Изучение зависимости случайной величины от ряда неслучайных и случайных величин приводят к моделям регрессии и регрессионному анализу на базе выборочных данных. Здесь соответствующий математический инструментарий в отличии от дисперсионного анализа не ставит своей целью установление причинной связи. Хотя, важно отметить, что гипотеза о причинной связи привносится из других теорий и дает возможность содержательно объяснить изучаемые явления.
Для одномерной (парной или множественной) регрессии одна случайная величина (зависимая переменная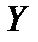 
) зависит от ряда неслучайных факторов, которые представлены независимыми переменными 
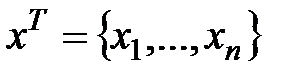и от набора случайных величин 
:
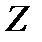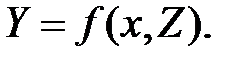
Примером регрессионной зависимости может служить зависимость между урожайностью определенной сельскохозяйственной культуры и влияющими на нее природными и экономическими факторами. Здесь из внестатистических соображений известно, что дожди влияют на урожай, а не наоборот. Следовательно, необходимо изучать зависимость урожайности от дождей и других природно-экономических факторов.
Исходным пунктом приложений регрессионного анализа является ситуация, которую можно описать следующим образом:
1. Объект исследования, как и прежде, представляется наблюдаемыми величинами (признаками)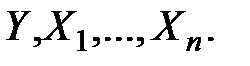 
2. Между ними предполагается наличие объективной связи. На основе процедур анализа ковариаций (ANCOVA) может быть установлено, что связь между наблюдаемой величиной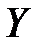 
и наблюдаемыми величинами 
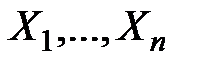действительно имеет место.
|
|
|
3. В простейшем случае, очевидно, не особенно рассчитывая на высокую степень адекватности, предполагается, что в принципе эту связь между зависимой величиной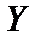 
и независимыми переменными 
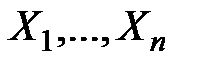можно представить функцией.
Очевидно, что, если такая функциональная зависимость в принципе действительно существует в природе, то ее точное аналитическое выражение узнать невозможно, а наблюдаемые эмпирические значения ее параметров можно только аппроксимировать. Тогда, по объективным причинам наблюдаемые данные в любом случае будут отклоняться от этой функции.
Для простоты рассуждений будем рассматривать простейшую зависимость в виде линейной функции. Отклонения включаются в модель, причем предполагается, что линейная функциональная связь между наблюдаемыми величинами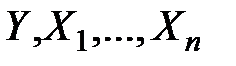 
дополняется аддитивной случайной переменной 
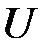, которая описывает эти случайные отклонения.
Таким образом, линейное уравнение функциональных связей, называемое регрессионным уравнением, имеет следующий вид
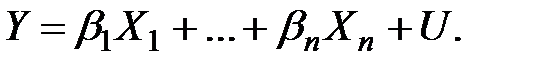(1.12)
Значения наблюдаемых величин при оценке параметров модели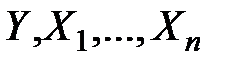 
считаются заведомо известными, т.е. по каждой из этих наблюдаемых величин имеется ряд данных (временной или пространственный). Значение случайной переменной 
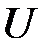и истинное значение каждого из параметров 
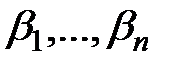в каждом конкретном случае неизвестны.
|
|
|
Основная цель регрессионного анализа –теоретически обоснованный и статистически надежный точечный и интервальный прогнозы зависимой переменной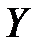 
. Для этого необходимо определить оценки отдельных регрессионных коэффициентов 
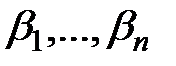относящихся к наблюдаемым переменным 
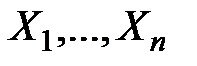и другие статистические характеристики.
Классическая процедура одношагового метода наименьших квадратов (1МНК).Имеющиеся ряды наблюдений по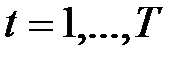 
позволяют для каждого из таких наблюдений получить соотношение
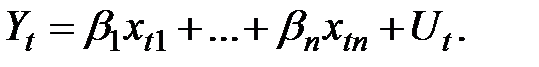(1.13)
Случайность возмущений 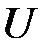делает регрессионную функцию стохастической.
Ряды данных (наблюдений) длиной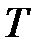 
для переменной 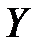и каждой из переменных 
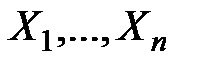необходимы для того, чтобы получить статистические оценки параметров модели. Количество рядов равно 
в каждойиз 
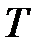точек наблюдения: 
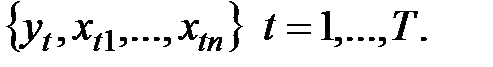Подставляя наблюдения 
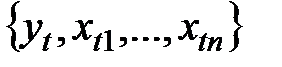для каждого 
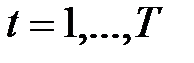получим систему соотношений
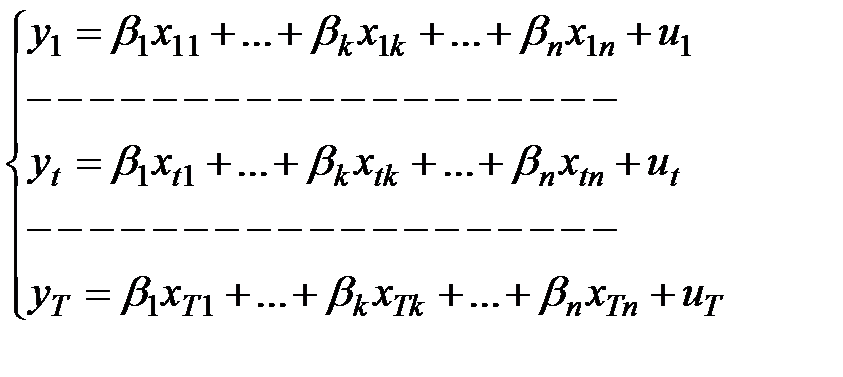. (1.14)
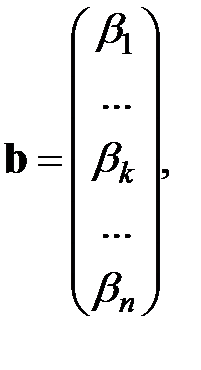
Далее введем обозначения:
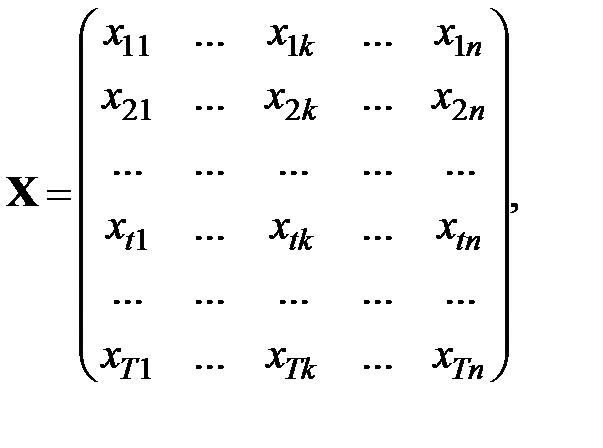
мерный вектор 
мерная матрица
,
мерныйвектор 
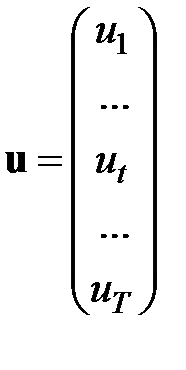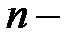мерныйвектор
|
|
|
и (1.14) можно записать в векторномвиде: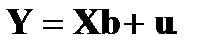 
Матрица 
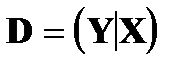называется матрицей исходных данных. Ее элементы «шкалируются» относительно фиксированных значений одного из фактор-признаков (например, первого).
Далее к обеим частям соотношения (1.12)применим оператор математического ожидания и получим:
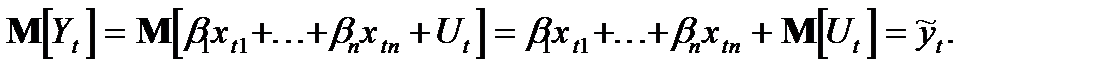
Величину, которую можно прогнозировать с помощью регрессионного уравнения.
При оценке параметров регрессионной функции применяется принцип минимума суммы квадратов ошибок (отклонений).
Алгоритм вычислений.
1. Формирование целевой функции. Вычисляются:
Ошибка или отклонение: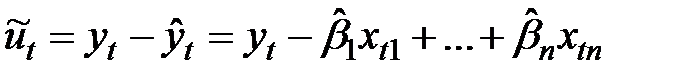 
;
Квадрат ошибки: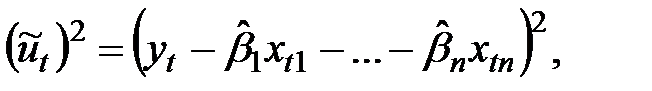 
Здесь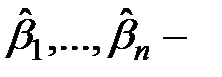 
значения параметров, получаемые в результате оценок.
Сумма квадратов ошибок:
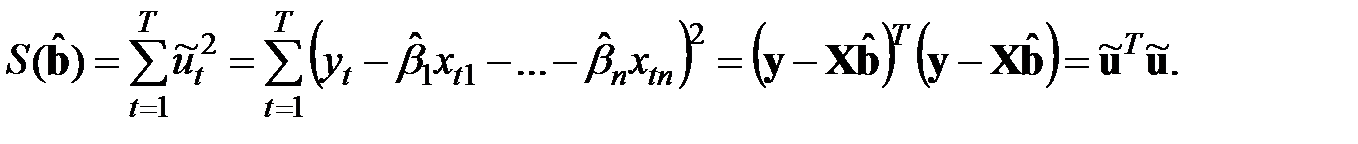
Это и есть целевая функция. Представим ее в виде:
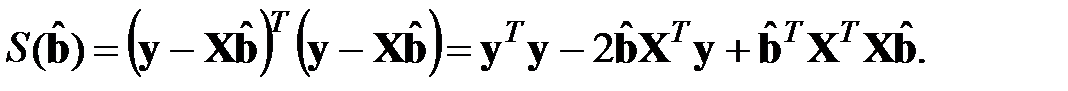
Далее, следуя необходимому условию экстремума функции многих переменных, вычислим частную производную целевой функции и приравняем ее нулю.
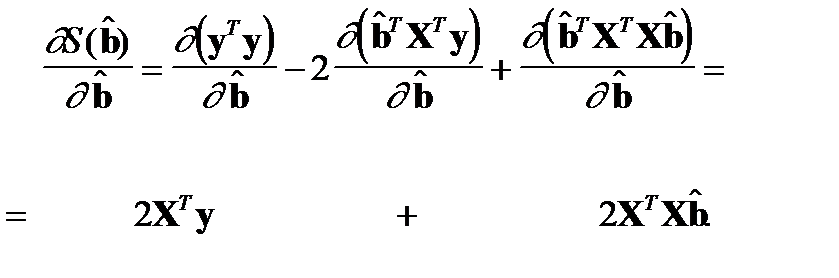
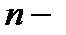мерный вектор 
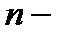мерный вектор
Необходимый признак:
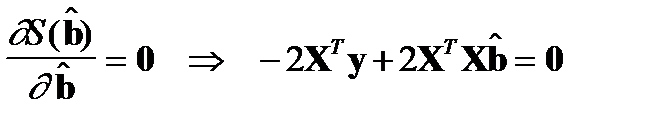
или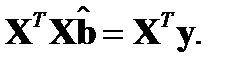 
В матричном виде:
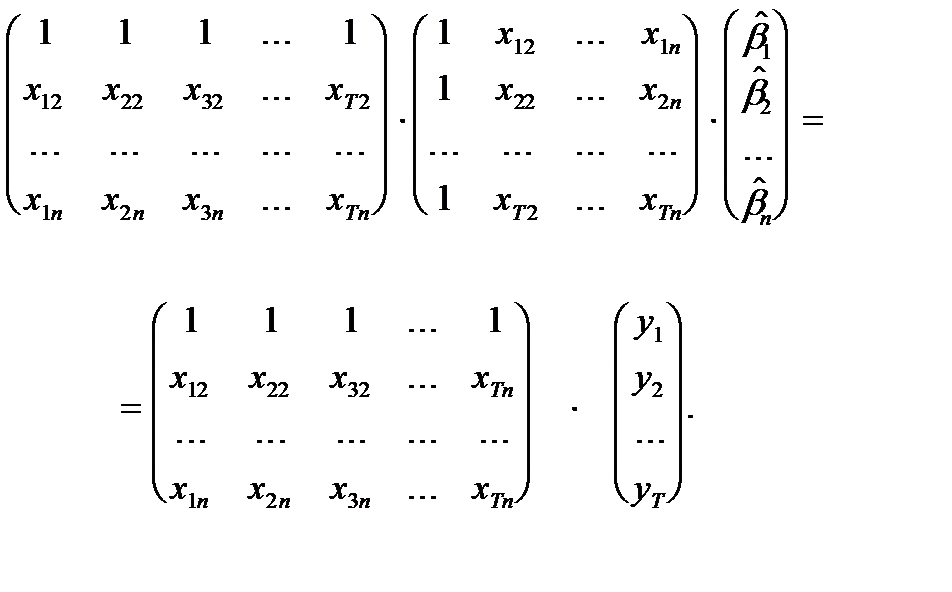
Здесь неизвестным (искомым) является вектор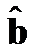 
. В векторной записи имеем:
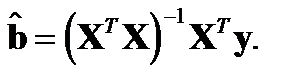
Подставляя найденные значения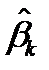 
в оцениваемое регрессионное уравнение, получим так называемую эмпирическую регрессионную функцию:
|
|
|
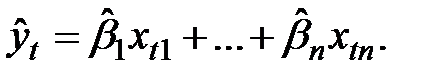(1.15)
С учетом того, что эмпирическая функция регрессии линейная, то дифференцирование ее по каждому из признаков (по переменным 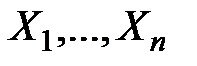) получим соответствующий эмпирический регрессионный коэффициент 
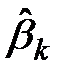в выражении (1.15). Таким образом, изменение этого 
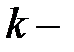го слагаемого на единицу, при прочих равных условияхвызовет изменение оцениваемой величины 
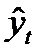на величину равную 
.
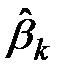В качестве иллюстрации рассмотрим пример, где одношаговый метод наименьших квадратов в экспресс-режиме дает возможность получить результат в виде (1.12).
Пример 1.2.Проведена оценка процессоров 10-ти рабочих станций локальной сети, построенной на базе машин приблизительно одного типа, но разных производителей (что предполагает некоторые отклонения параметров работы машин от базовой модели). Для тестирования работы процессоров использована смесь типа ICOMP 2.0 в основу, которой положены два основных теста:
1. 125.turb3D – тест моделирования турбулентности в кубическом объеме (прикладное ПО);
2. NortonSI32 –инженерная программа типа AutoCaD.
Вместе со смесью был применен вспомогательный тест для нормирования времени обработки данных SPECint_base95. Оценка процессоров производилась по взвешенному времени выполнения смеси, нормированному по эффективности базового процессора, в соответствии с формулой
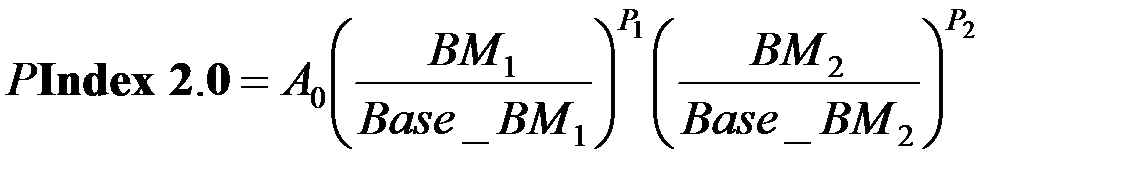, (1.15)
где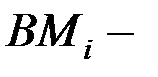 
время выполнения 
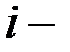го теста;
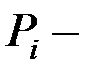вес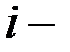 
го теста;
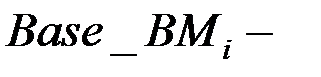эффективность базового процессора на 
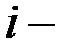м тесте.
Если выражение (1.15) логарифмировать, то получим:
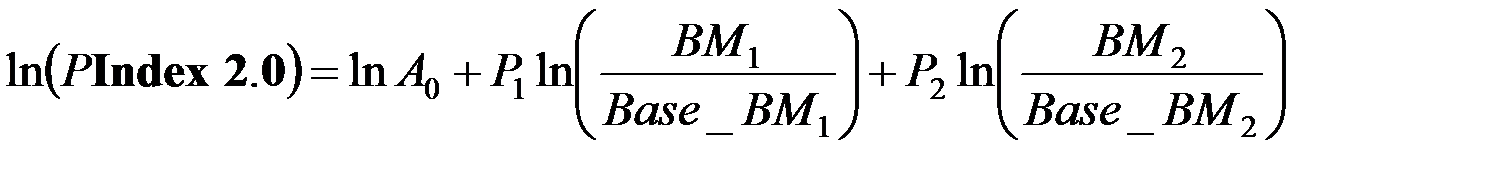
и после переобозначения переменных:
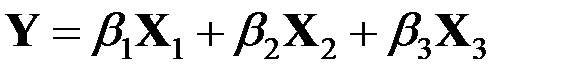. (1.16)
Здесь:
;
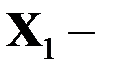базовое время обработки теста SPECint_base95 
;
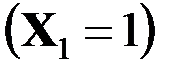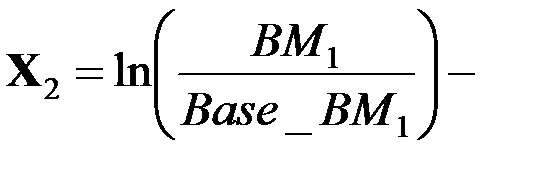логарифм времени обработки первого теста, 
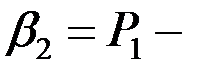регрессионный коэффициент, получаемый в оценках (вес теста);
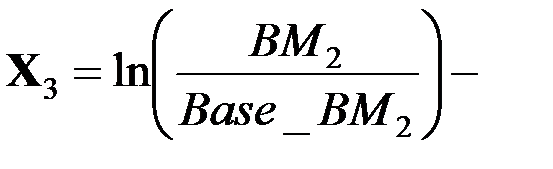логарифм времени обработки второго теста, 
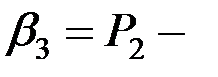регрессионный коэффициент, получаемый в оценках (вес теста);
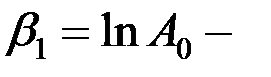регрессионный коэффициент – вес теста обработки арифметических операций в целых числах (базовый тест).
По данным измерений, приведенным в таблице, построить регрессионную (эмпирическую) функцию, оценить коэффициенты регрессии и проверить модель на адекватность (вычислить ковариационную матрицу, коэффициенты парной корреляции, коэффициент детерминации).
В таблице 1.3 приведены результаты в масштабе единиц общего выделенного признака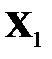 
:
Таблица 1.3 – Результаты замеров в масштабе единиц первого признака
| № п/п |  =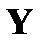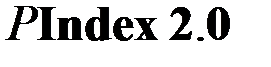 
|  = 
|  = 
|
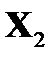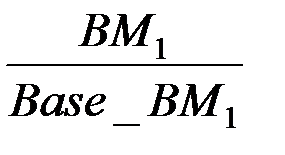
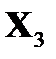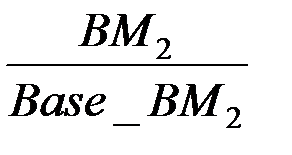
| 1 | 2 | 3 | 4 |
| 1 | 3,5 | 45,0 | 60,0 |
| 2 | 6,0 | 55,0 | 36,0 |
| 3 | 5,0 | 50,0 | 36,0 |
| 4 | 3,5 | 40,0 | 55,0 |
| 5 | 1,5 | 20,0 | 90,0 |
| 6 | 2,5 | 25,0 | 75,0 |
| 7 | 2.0 | 20,0 | 80,0 |
| 8 | 3,0 | 30,0 | 70,0 |
Очевидно, будем иметь для указанных данных в соответствии с алгоритмом:
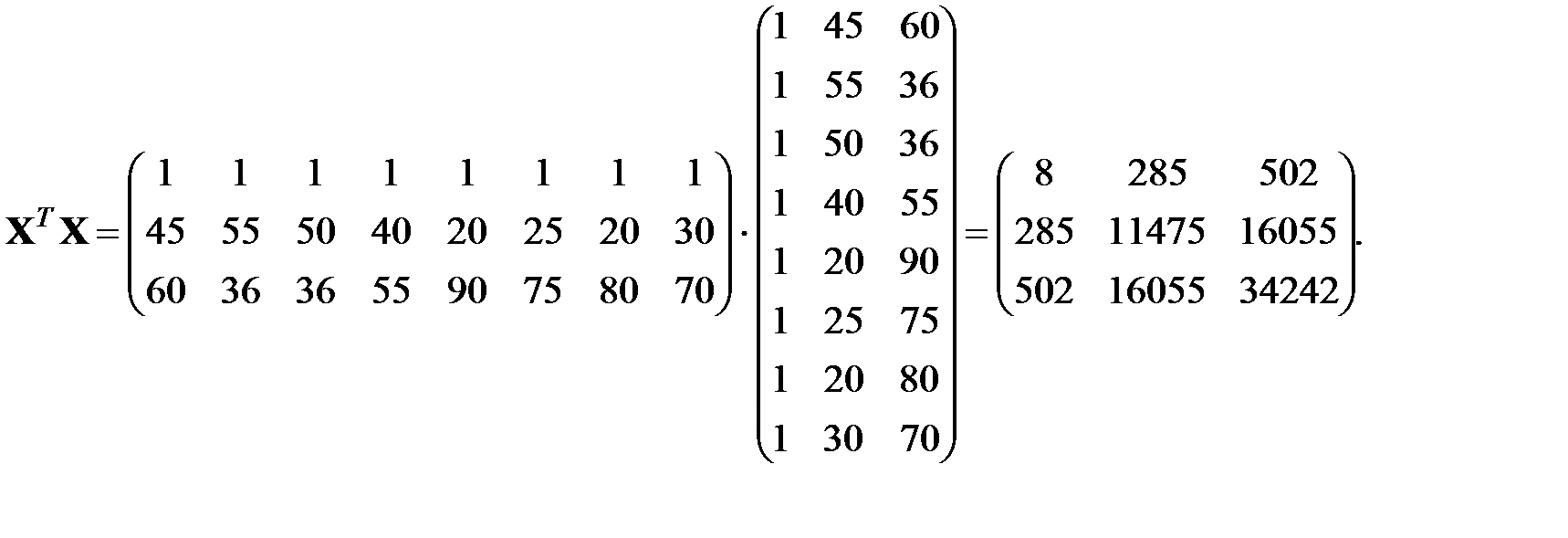
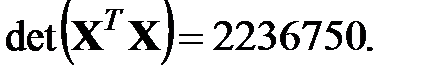
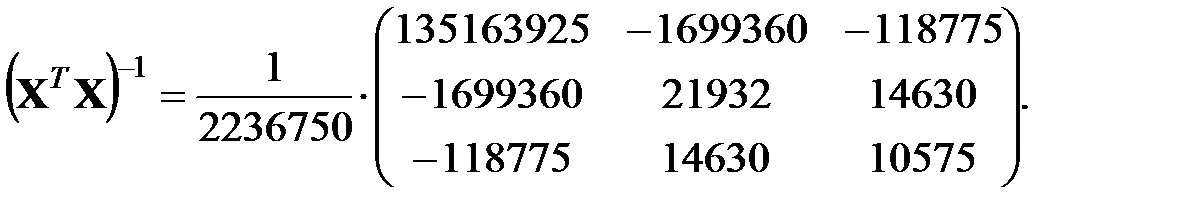
Вектор правой части системы нормальных уравнений Гаусса определяется следующим образом (в матричной форме):
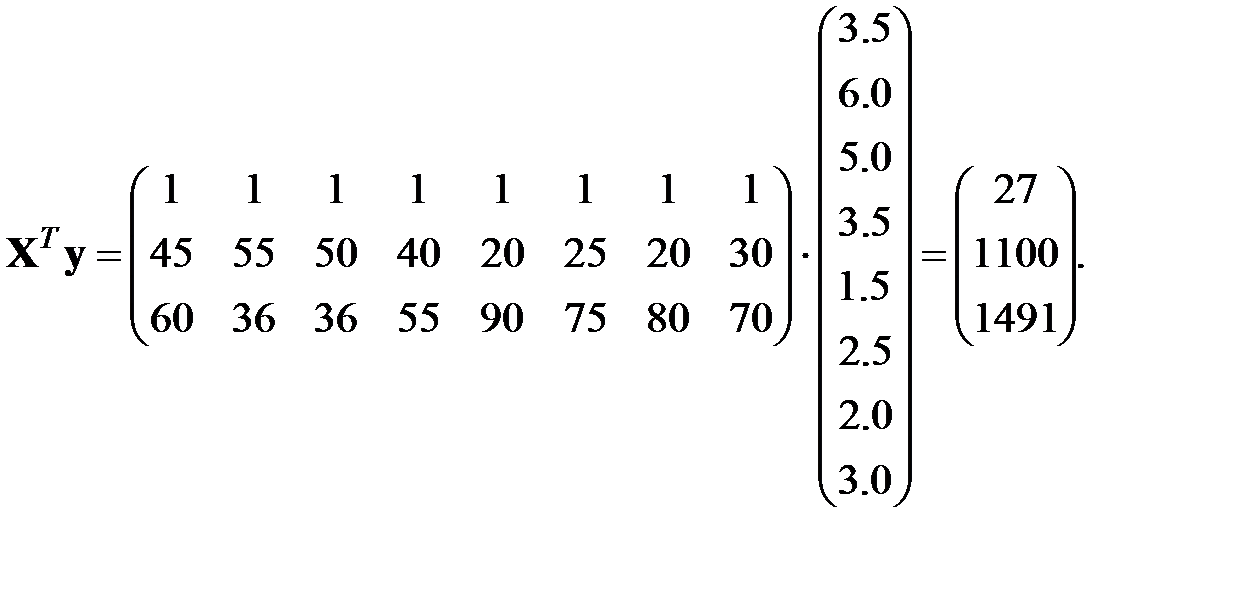
Численные значения компонентов вектора регрессионных коэффициентов, оцененные методом наименьших квадратов:
Сама эмпирическая двухфакторная регрессиябудет иметь вид:
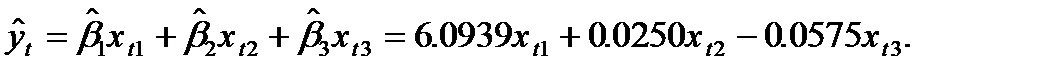
Она приводит к следующим прогнозным (расчетным) значениям регрессанда:
Далее рассчитываем компоненты вектораотклонений
и математическое ожидание вектора ошибок:
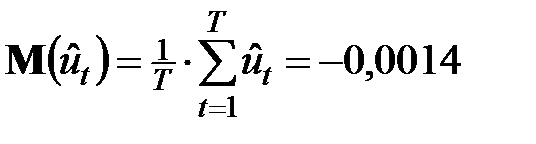
Близость его значения к нулю свидетельствует о том, что расчеты выполнены верно. Как уже было указано, оценки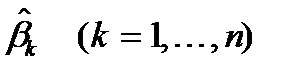 
носят случайный характер, однако, при этом не исключается, что среди них имеется объективная связь. На этом этапе исследований собственно и включается ядро процедуры метода ANCOVA.
По определению, характеристикой взаимосвязи двух случайных величин является их ковариация. Известно, чтоковариацией случайных величин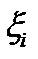 
и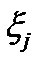 
называется число 
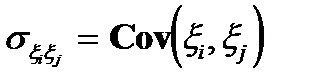равное математическому ожиданию произведения отклонений случайных величин 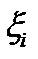и 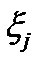от своих математических ожиданий: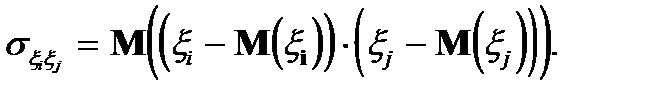 
Согласно этому определению ковариации, для совокупной характеристики оценок 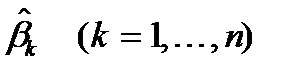, дисперсии 
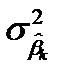и ковариации 
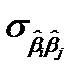, запишем в виде так называемой ковариационной матрицы:
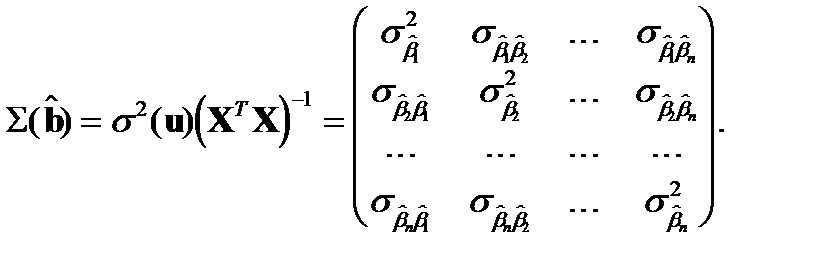
Ковариационная матрица по эмпирическим данным может быть получена Она неизвестна и может быть лишь оценена.
Оцененная матрица: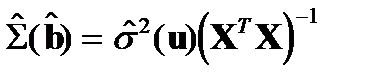 
, где 
Возвращаясь к примеру, укажем, что
и рассчитаем величину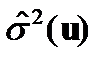 
следующим образом:
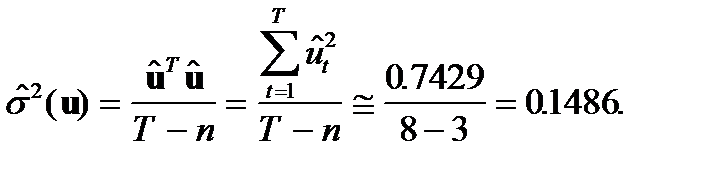
Тогда:
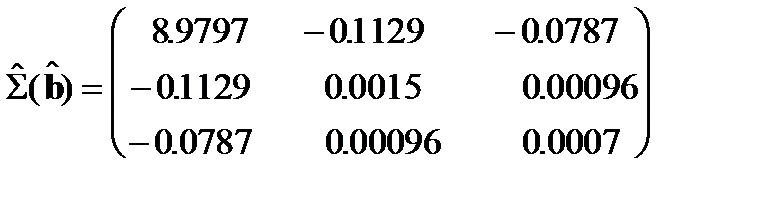
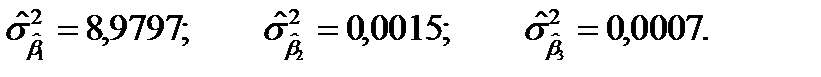
Об уровне связи между оцененными параметрами можно говорить более конкретно, если рассчитать коэффициенты парной корреляции
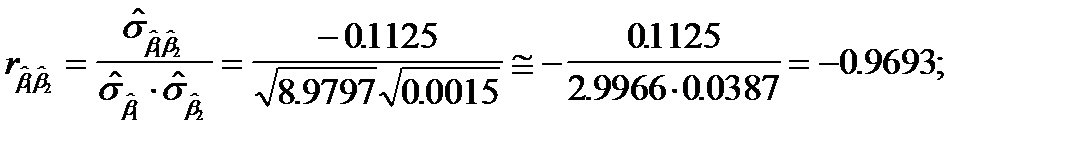
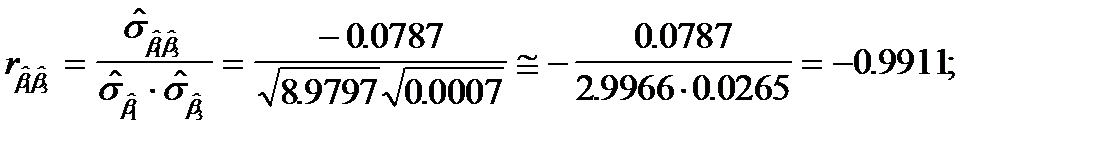
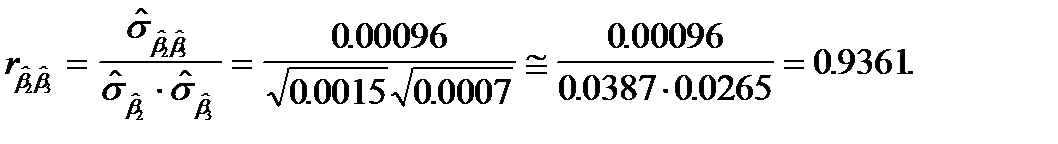
Их значения по абсолютной величине близки к единице. Это свидетельствует о том, что между параметрами существует достаточно тесная связь.
Важно заметить, что более существенная роль ковариационному анализу отводится при исследованиях авторегрессионных процессов.
Известно, чтоавтокорреляция возмущений означает, что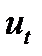 
в регрессионном уравнении для периода 
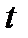зависит от возмущений более ранних периодов в том же уравнении. Для простейшего случая, когдаимеет место авторегрессионный процесс первого порядкаимеем определение.
Определение: Возмущение 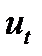подчиняется авторегрессионному процессу первого порядка, если выполняются следующие условия:
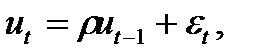где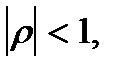 
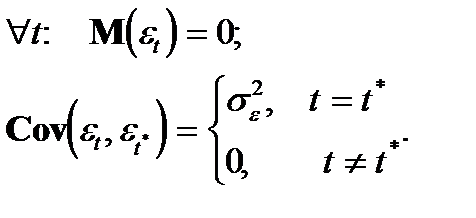(1.17)
Здесь ковариационная матрица, которая имеет следующий вид:
( 
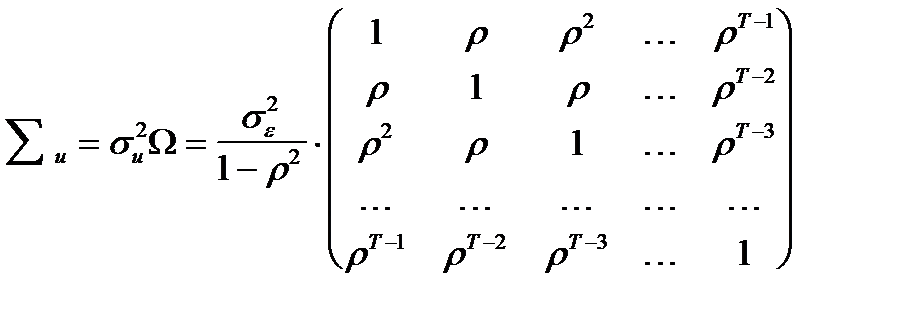
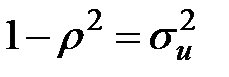), непосредственно используется для очистки модели от авторегресси при использовании процедуры метода Эйткена.
Дата добавления: 2018-06-27; просмотров: 833; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!