ОПИСАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ ЭМПИРИЧЕСКИХ ДАННЫХ: ANCOVA И
РЕГРЕССИОННЫЙ МЕТОД
Дисперсионный анализ
Суть метода заключается в исследовании влияния одной или нескольких качественных переменных (признаков или, как принято говорить, – факторов-признаков) на одну зависимую (количественную) переменную (отклик). В основе такого исследования лежит гипотеза, что одни переменные могут рассматриваться как причины (независимые переменные):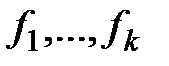 
, а другие как следствия (зависимые переменные). В эксперименте независимыми переменными исследователь может варьировать и, соответственно, иметь разные уровни отклика.
Отсюда и основная цель – определение уровня значимости различий между значениями средних на основе сравнения дисперсий. Здесь общая дисперсия делится на несколько источников, а далее дисперсия, вызванная различиями между группами данных, сравнивается с дисперсией, которая опосредована внутригрупповой изменчивостью.
Основная гипотеза, если она верна, заключается в том, что оценка дисперсии, связанной с внутригрупповой изменчивостью, близка в определенном смысле к оценке межгрупповой дисперсии. Таким образом, общая дисперсия разбивается на компоненты, которые опосредованы влиянием вполне определенных факторов на исследуемый признак. Далее эти компоненты сравниваются друг с другом, определяется, какова доля общей вариативности результирующего признака обусловлена влиянием независимых фактор-признаков. Здесь используется известныйF-критерий Фишера.
|
|
|
Входными данными для проведения F-тестирования (собственно это основа дисперсионного анализа данных) являются данные исследования нескольких (трех и более) выборок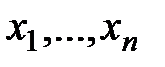 
, не обязательно равных по объему и, среди которых не учитывается присутствие объективных связей.
Важно отметить, что дисперсионный анализ относится к параметрическим методам, что обуславливает его применение лишь в тех случаях, когда точно известно, что закон распределения генеральной совокупности является нормальным. Кроме того, дисперсионный анализ применяется в том случае, если зависимая переменная измерена в шкалах отношений, интервалов или порядков. При этом сами регулярные переменные могут иметь нечисловую природу (шкала наименований).
В классической постановке задачи, решаемые методом дисперсионного анализа выглядят следующим образом. Пусть производится анализ влияния на случайную величину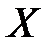 
фактора 
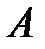, который исследуется на 
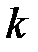уровнях: 
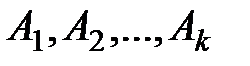. На каждом уровне 
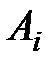произведено 
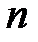наблюдений: 
, 
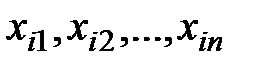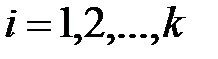случайной величины 
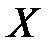. Таким образом, на всех 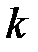уровнях фактора 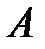в общей сложности произведено 
наблюдений.
Далее, расположим все данные экспериментов в таблицу (см. табл. 1.1):
|
|
|
Таблица 1.1 – Данные экспериментов
| Номер наблюдения | Уровни фактора | |||||
| 
| … | 
| … | 
| |
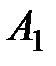
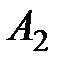
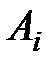
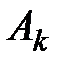
| 1 |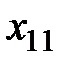 
| 
| … | 
| … | 
|
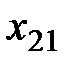
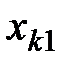
| 2 |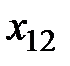 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
| 
| 
| … | 
| … | 
|
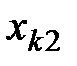
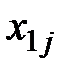
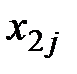
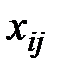
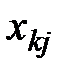
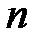
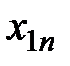
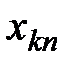
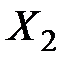
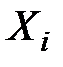
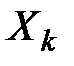
В табл. 1.1 обозначено: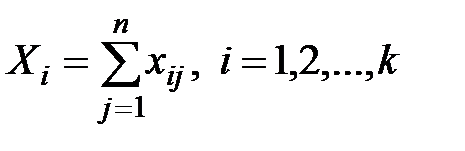 
.
Будем рассматривать оценки различных дисперсий. Для оценки дисперсии изменения данных на уровне 
(по строкам), получим
. (1.1)
Согласно предпосылкам дисперсионного анализа, должно выполняться равенство:
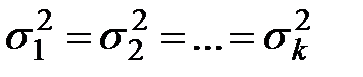. (1.2)
При выполнении (1.2) находим оценку дисперсии 
рассеяние случайной величины 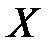вне зависимости от воздействий фактора :
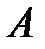. (1.3)
Оценка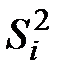 
имеет 
степень свободы, а оценка 
, соответственно 
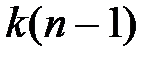степень. Оценка 
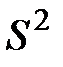выборочной дисперсии 
с использованием всех наблюдений равна:
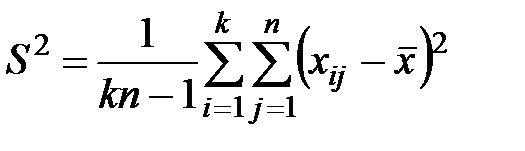. (1.4)
Здесь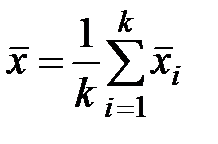 
, а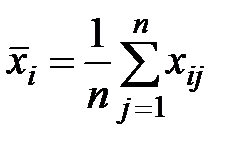 
.
Тогда
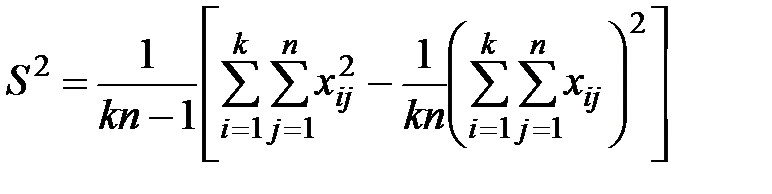. (1.5)
Введем в рассмотрение оценку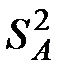 
дисперсии 
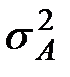, которая характеризует вариации математических ожиданий 
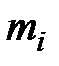под воздействием фактора .
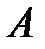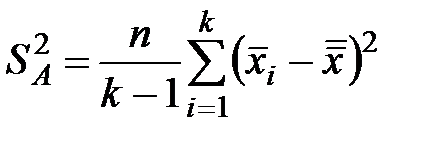. (1.6)
Заметим, что оценка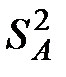 
имеет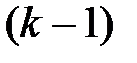 
степень свободы.
Исследование влияния фактора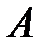 
на вариацию математических ожиданий 
, 
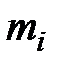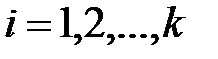сводится к процедуре сравнения дисперси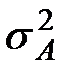й 
и 
. Их оценки соответственно 
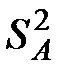и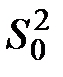 
. Считается, что фактор 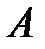значительно влияет на изменения математических ожиданий 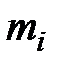, если значимо отношение 
. Оно значимо, если с достоверной вероятностью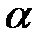 
:
|
|
|
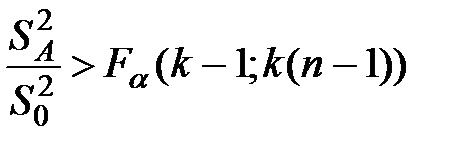. (1.7)
Здесь 
квантиль F-распределения Фишера с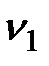 
и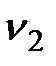 
степенями свободы. Значения 
квантиля можно найти по таблицам стандартных распределений.
Противный случай: влияние фактора 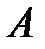незначимо, т.е. (1.7) не выполняется, а имеет место соотношение: 
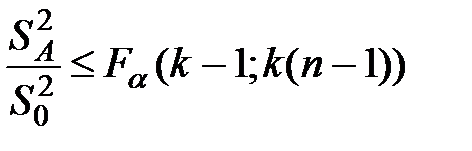, то для оценки дисперсии может быть применена более точная оценка 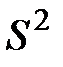с 
с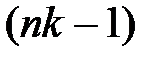тепенями свободы, против 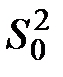с с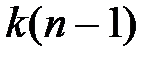тепенями свободы.
Алгоритм вычислений.
1. Вычисляются последовательно суммы
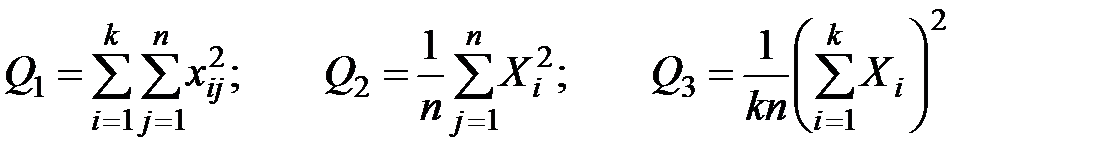. (1.8)
2. Вычисляются
. (1.9)
3. Сравниваются 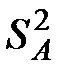и 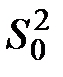. При этом устанавливается уровень значимости фактора 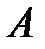. Если:
,
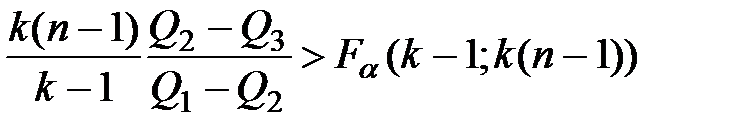то влияние фактора 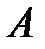считается значимым. В противном случае всю выборку можно считать однородной с общей дисперсией 
.
Замечание. Если на различных уровнях фактора 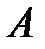производится разное число наблюдений (экспериментов), то формулы дисперсионного анализа примут вид:
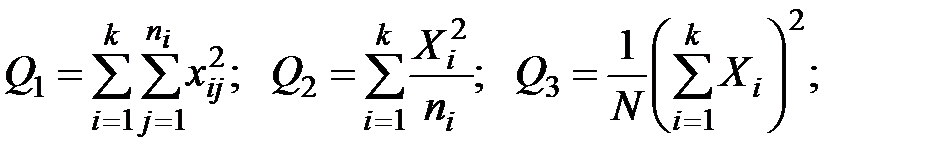(1.10)
|
|
|
. (1.11)
Здесь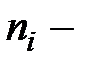 
количество наблюдений на уровне 
, 
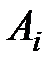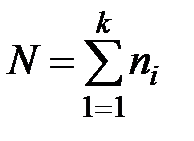. Отношение сравнивается с величиной квантиля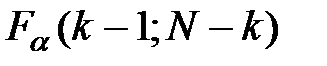 
.
В качестве иллюстрации выше сказанного, приведем пример.
Пример 1.1.Проведем дисперсионный анализ отвлеченных данных, представленных в таблице (см. табл. 1.2).
Таблица 1.2 – Исходные данных экспериментов
|
| Уровни фактора | ||||
| 
| 
| 
| 
| |
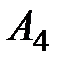
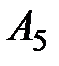
| 1 | 3,2 | 2,6 | 2,9 | 3,6 | 3,0 |
| 2 | 3,1 | 3,1 | 2,6 | 3,4 | 3,4 |
| 3 | 3,1 | 2,7 | 3,0 | 3,2 | 3,2 |
| 4 | 2,8 | 2,9 | 3,1 | 3,3 | 3,5 |
| 5 | 3,3 | 2,7 | 3,0 | 3,5 | 2,9 |
| 6 | 3,0 | 2,8 | 2,8 | 3,3 | 3,1 |
| S | 18,5 | 16,8 | 17,4 | 20,3 | 19,1 |
1. 
2. 
3. 
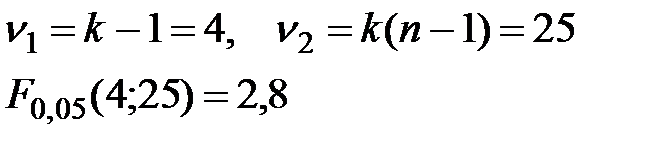
Так как 
влияние фактора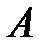 
на поведение наблюдаемой случайной величины признается значимым.
Дата добавления: 2018-06-27; просмотров: 328; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!