Зв'язок між декартовими та полярними координатами
Пару полярних координат r та φ можна перевести в Декартові координати x та y шляхом застосування тригонометричних фукнцій синуса та косинуса:
x = r cosφ
y = r sin φ,
в той час як дві Декартові координати x та y можуть бути переведені в полярну координату r:
r2 = y2 + x2 (за теоремою Піфагора).
Для визначення кутової координати φ, слід взяти до уваги два такі міркування:
· Для r = 0, φ може бути довільним дійсним числом.
· Для r ≠ 0, аби отримати унікальне значення φ, слід обмежитись інтервалом в 2π. Зазвичай, обирають інтервал [0, 2π) або (−π, π].
Для обчислення φ в інтервалі [0, 2π), можна скористатись такими рівняннями (arctg позначає обернену функцію до тангенсу):
Тривимірне розширення
Полярна система координат поширюється в третій вимір двома системами: циліндричною та сферичною, обидві містять двовимірну полярну систему координат як підмножину. По суті, циліндрична система розширює полярну додаванням ще однієї координати відстані, а сферична — ще однієї кутової координати.
Циліндричні координати
Точка P накреслена в циліндричній системі координат.
Циліндрична система координат, грубо кажучи, розширює пласку полярну систему додаванням третьої лінійної координати, що має назву висоти і дорівнює висоті точки над нульовою площиною подібно до того, як Декартова система розширюється на випадок 3-х вимірів. Третя координата зазвичай позначається як z, утворюючи трійку координат (ρ, φ, z).
|
|
|
Трійку циліндричних координат можна перевести в Декартову систему такими перетвореннями:
x = ρ cosφ
y = ρ sinφ
z = z .
Сферичні координати
Точка накреслена в сферичній системі координат.
Також полярні координати можна розширити на випадок трьох вимірів шляхом додавання кутової координати θ, що дорівнює куту повертання від вертикальної вісі z (називається зенітом або широтою, значення знаходяться в інтервалі від 0 до 180°). Тобто, сферичні координати, це трійка (r, θ, φ), де r — відстань від центру координат, φ — кут від осі x (як і в пласких полярних координатах), θ — широта. Сферична система координат подібна до географічної системи координат для визначення місця на поверхні Землі, де початок координат збігається з центром Землі, широта δ є доповненням θ і дорівнює δ = 90° − θ, а довгота l обчислюється за формулою l = φ − 180°.
Трійку сферичних координат можна перевести в декартову систему такими перетвореннями:
Перехід до інших систем координат
Від сферичних до Декартових:
Від Декартових до сферичних:
(тут, звісно, потрібне уточнення для значень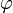 
поза першим квадрантом; те ж саме для всіх формул з арктангенсом тут і нижче; однак, заміна на відповідну формулу з арккосинусом знімає це питання по відношення до координати θ).
|
|
|
Модуль якобіана перетворення від декартових до сферичних координат:
| J | = r2sin θ.
Дата добавления: 2018-06-27; просмотров: 3247; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!