Гидромониторные струи и их воздействие на разрушаемую долотом породу.
17.1. Экспериментальные исследования промывочных узлов
гидромониторных долот и затопленных струй
17.1.1. Экспериментальная установка и методика исследований
Наиболее полные исследования струй и испытания гидромониторных насадок проведены под руководством А.К. Козодоя на опытной установке института ВолгоградНИПИнефть, схема которой показана на рис. 17.1. В корпусе 1 смонтирована подвижная часть - центральная труба 2 со штурвалом 3, на нижнем конце которой с помощью накидной гайки крепится насадка 5. В днище корпуса 6 помещена соосно с насадкой 5 трубка Пито 7. Пространство между насадкой и трубкой Пито образует рабочую камеру-тупик. В выкидной линии 8 установлен штуцер 9 для создания заданного планом эксперимента противодавления в рабочей камере. Подводящий канал к насадке образуется патрубком 10. Давление измерялось образцовыми манометрами 4.
В качестве рабочего агента использовались вода или водные растворы полимеров, например, КМЦ, с добавкой иногда ПАВ. Жидкость, не обладающая абразивными свойствами, подавалась в установку многоступенчатым центробежным насосом с приводом от синхронного электродвигателя мощностью 350 кВт, способным развивать давление до 6,5 МПа при расходе до 50 дм3/с. После стенда жидкость попадала в мерную емкость (при замерах расхода объемным способом) и в сливную емкость, откуда возвращалась в приемные емкости другим, низконапорным, центробежным насосом.
|
|
|
Промывочные системы долот и скоростные поля отраженных от забоя потоков исследовались на другой, аналогичной по схеме потока жидкости установке, имеющей увеличенный по внутреннему диаметру корпус, достаточный для размещения долота диаметром 215,9 мм. Обе установки были унифицированы по размерам входного и выходного патрубков, что упрощало замену установок и подсоединение измерительных систем.
Конструкции опытных установок позволяли испытывать любые модельные (изготовленные из стали) или натурные (минералокерамические) насадки при скоростях истечения, как правило, не менее 70...80 м/с, что обеспечивало испытание струй, насадок и промывочных узлов долот в условиях развитой турбулентной автомодельности (при Re > 8*105).
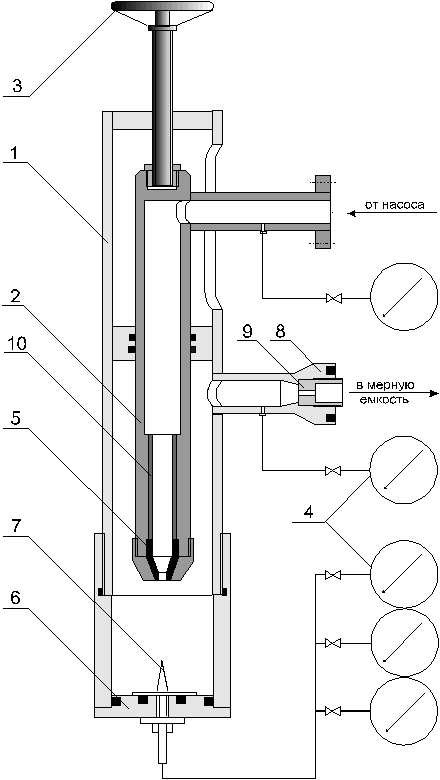
Рис. 17.1. Схема стенда для испытания насадок и исследования
затопленных гидромониторных струй.
То обстоятельство, что насос мог развивать давление до 6,5 МПа практически при любых расходах (вплоть до 50 дм3/с), давало возможность (при сохранении турбулентной автомодельности) использования части этого давления для моделирования забойных условий истечения струй, для обеспечения бескавитационного истечения струй из насадок в стендовых условиях. Достигалось это созданием противодавления с помощью штуцера 9, установленного в быстросъемном соединении выкидной линии 8.
|
|
|
17.1.2. Исследование гидравлических сопротивлений промывочных узлов гидромониторных долот
Преобразование перепада давления на долоте pд в кинетическую энергию гидромониторных струй, оцениваемую величиной начального гидродинамического давления струй po в наиболее узком сечении проточной части насадок, сопровождается потерями на входе в промывочное отверстие долота (в подводящем канале) и в сменной гидромониторной насадке. Именно по этой причине отношение po/pд всегда меньше 1. Уменьшение этих потерь и точный их расчет являются непременными условиями рационального использования забойной гидравлической энергии и определения оптимальных режимов промывки скважины.
Для оснащения гидромониторных долот применяются так называемые “короткие” насадки, протяженность проточной части которых, как правило, меньше наружного диаметра насадки.
Одним из параметров, используемых для оценки гидродинамического совершенства промывочной системы гидромониторного долота, является коэффициент расхода промывочного узла μд, физический смысл которого ясен из формулы для определения перепада давления на долоте:
|
|
|
 ,
,
где fд – суммарная площадь сечения отверстий насадок,
ρ – плотность буровой промывочной жидкости,
Q – расход промывочной жидкости.
Квадрат μд является величиной, близкой по смыслу к к.п.д. превращения перепада давления рд (потенциальной энергии) в гидродинамическое давление струи ро (кинетическую энергию) в предположении, что энергия струи используется в дальнейшем полностью, а не теряется на интенсивное перемешивание жидкости и ее нагревание на забое (что, строго говоря, и происходит). По этой причине μд всегда меньше 1. Чем μд больше и ближе к 1, тем меньше потери давления в промывочном узле долота.
В любом гидромониторном долоте общие потери давления, как уже выше отмечалось, распределены на два последовательно расположенного местного сопротивления: в подводящем канале и в самой гидромониторной насадке соответственно с коэффициентами расхода μп и μн.
Стендовыми испытаниями были решены задачи:
- экспериментальное определение величин коэффициентов расхода упомянутых выше элементов промывочного узла долот при наличии противодавления и при его отсутствии;
|
|
|
- оценка влияния условий истечения (притиводавления и стесненности струи) и конструктивных особенностей проточной части коротких насадок на величину их коэффициентов расхода;
Цели испытаний:
- повышение точности расчетов перепада давления на долоте и начальных гидродинамических давлений струй;
- обоснование требований к конструктивному оформлению высокосовершенных в гидравлическом отношении промывочных узлов долот и определение возможностей минимизации габаритных размеров насадок без ущерба для их качества.
Прежде, чем приступить к изложению и анализу результатов стендовых испытаний, проанализируем распределение потерь давления для случая применения в долоте равноразмерных насадок, когда скорости истечения струй vo из разных насадок одинаковы и перепад давления на долоте pд равен перепаду давления pпк в любом из промывочных каналов. Перепад давления на долоте в этом случае будет равен:
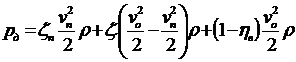 , (17.1)
, (17.1)
где vп и vo - соответственно скорость потока в подводящем канале и максимальная скорость в наиболее узком сечении насадки;
zп и zн - коэффициенты “местных” сопротивлений подводящего канала и насадки;
hв - коэффициент восстановления давления (коэффициент обратного превращения в насадке части скоростного напора v2o r / 2 в давление);
r - плотность бурового раствора.
После замены vп =vo fo / fп (из условия постоянства расхода жидкости через канал) получим выражение:
 , (17.2)
, (17.2)
где fo и fп - площади сечения отверстий насадки и подводящего канала.
С другой стороны -
 , (17.3)
, (17.3)
где mд - коэффициент расхода промывочной системы долота.
В результате получаем
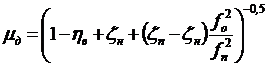 . (4.2.4)
. (4.2.4)
В общем случае промывочный узел долота состоит из двух участков: участка сужения потока (включая сужение при входе в подводящий канал), на котором и происходит основное превращение потенциальной энергии в кинетическую, и выходного участка, чаще всего цилиндрического, расположенного после самого узкого сечения, который призван выравнить профиль скоростей струи на выходе из насадки.
Третья и четвертая слагаемые в скобках формулы (17.4) выражают потери давления на первом участке и потому всегда больше нуля. Что касается hв, то этот коэффициент зависит от наличия и формы второго участка, и он заведомо равен нулю в двух случаях: когда нет второго участка (цилиндрического спрыска) или когда нет за насадкой давления. Поэтому в оговоренных случаях mд заведомо должен быть меньше 1. Для того, чтобы коэффициент расхода mд стал больше 1, необходимо выполнение условия:
 , (17.5)
, (17.5)
что возможно, в свою очередь, при одновременном соблюдении двух условий: наличия за насадкой абсолютного давления, равного или превышающего величину “возвращаемого” давления, и наличия в насадке условий для полного или частичного превращения скоростного напора в давление (например, наличие раструба - диффузора - после наиболее узкого сечения и цилиндрического участка). Итак, если струя из насадки истекает в среду с “достаточным” противодавлением и если при этом выходное сечение насадки больше самого узкого сечения в ней, а потери давления в промывочном канале в целом меньше “восстановленного” давления, то mд вполне может стать больше 1. В общем случае, следовательно, если коэффициент расхода определяется по самому узкому сечению в промывочном канале, mд может быть как меньше, так и больше 1.
Объектами испытаний были:
“Цилиндрические” насадки с “острым” (без фаски или закругления) входом в цилиндрический канал (рис. 17.1а, б ). Внутри группы насадки отличались относительной длиной насадки: отношением длины цилиндрического отверстия lц кдиаметру отверстия do .
Конические насадки без плавного сопряжения конической поверхности с цилиндрической (рис. 17.2а, б). Внутри группы насадки отличались углом конуса j, наличием (или отсутствием) цилиндрического участка на входе и длиной цилиндрического участка на выходе (цилиндрического спрыска) lц. Необходимость в устройстве цилиндрического участка на входе возникала, когда задавались большими j и относительно малыми lц , а длина насадки при этом оставалась неизменной.
Конические насадки, имеющие плавное сопряжение поверхностей с разными радиусами скругления (рис. 17.2а, б), которые так же, как и насадки второй группы имели разные j и lц .
Насадки с криволинейным профилем, заканчивающимся цилиндрическим спрыском: эллиптическая, радиальная и бирадиальная (коноидальная). Они показаны на рис. 17.3а, б, в.
Насадка с “профилем естественного износа”, воспроизводящая профиль, который формируется через определенное время при прокачке через стальную цилиндрическую насадку абразивной жидкости, например, глинистого раствора, содержащего песок (рис. 17.3г).
Насадки минералокерамические удлиненные.
Гидромониторное долото, оснащенное либо специально изготовленными стальными насадками, либо стандартными минералокерамическими.
Насадки третьей, четвертой и пятой групп можно отнести к одному классу “плавных” насадок, у которых профиль сужения составлен из поверхностей, плавно сопрягающихся между собой, в том числе с цилиндрическим спрыском.
Все насадки первых четырех групп изготовлялись из стали и имели одинаковую длину - 20 мм. В редких случаях, когда запланированный профиль не “вписывался” в длину 20 мм, например, при j = 140 , насадка имела длину, превышающую 20 мм.
Насадка с “профилем естественного износа” отличалась от всех остальных тем, что была самой короткой, имела длину, равную 11 мм.
Всего испытано 46 различных вариантов насадок, отличающихся или типом профиля (конический без сопряжения поверхностей канала, конический с сопряжением, эллиптический и т.п.), или длиной цилиндрического участка, или углом конуса на участке сужения. Описания этих насадок даны в Приложении. Кроме того, испытаны четыре варианта промывочного узла гидромониторных долот, в том числе долота без насадок.
Во всех опытах критерий Re на срезе насадки был не менее 0,7* 106 и чаще всего находился в пределах 0,9×106 ... 1,1×106 , что дает право относить результаты к области турбулентной автомодельности.
Технические характеристики описанной в подразделе 17.1 опытной установки позволяли проводить испытания насадок и исследование струй в условиях, воспроизводящих натурные как по размерам насадок, так и величинам перепада давления на долоте и в среде истечения. В этой ситуации установление влияния абсолютного давления среды в тупике, в который истекает сформированная насадкой струя, на коэффициент расхода насадки mн или промывочного узла долот mд является важнейшей с практической точки зрения задачей.

Рис. 17.1. Насадки цилиндрические с остроугольным входом:
а- короткая (диафрагма);
б - длинная (длина больше диаметра отверстия).

Рис. 17.2. Конические насадки без плавного сопряжения
конического и цилиндрического поверхностей:
а - без цилиндрического входа;
б - с цилиндрическим входом.
Первые же испытания цилиндрических и конических насадок показали, что существует критическое значение отношения абсолютного давления среды pа.пд к начальному гидродинамическому давлению струи po в выходном сечении насадки pпд*кр = pа.пд / pо , при превышении которого коэффициент расхода насадки mн остается постоянным. В интервале 0 < pп*д < pп*д.кр коэффициент mн увеличивается от mн.а до некоторого “стандартного” значения mн.ст . Стендовые испытания показали, что для конических насадок без сопряжения конической и цилиндрической поверхностей (в дальнейшем для краткости: “коническая насадка без скругления”) pп*д.кр = 0,4, а для цилиндрических - 0,85. Исходя из этого все последующие исследования с целью определения стандартных значений mн.ст для различных насадок, имеющих сужающийся канал (не цилиндрических), проведены при pп*д > 0,5 (чаще всего при pп*д > 0,7) , что заведомо больше pп*д.кр для любых возможных вариантов насадок с сужающимся профилем.
 Тот факт, что у конических насадок без скругления mн зависит от давления в среде истечения, означает, что если бы такие насадки применялись до некоторой глубины, то mн был бы переменной величиной, зависящей от глубины бурения. Предположим, что планируемый перепад давления pд равен 10 МПа. Тогда pпд.кр = 0,4pд = 4 МПа, что приблизительно соответствует глубинам 360...380 м (в зависимости от плотности жидкости и потерь давления в заколонном пространстве). Следует однако оговориться, что описанный эффект, как будет показано дальше, минимален у насадок с плавным профилем и потому нет практической необходимости вносить поправку величины mн с учетом глубины бурения.
Тот факт, что у конических насадок без скругления mн зависит от давления в среде истечения, означает, что если бы такие насадки применялись до некоторой глубины, то mн был бы переменной величиной, зависящей от глубины бурения. Предположим, что планируемый перепад давления pд равен 10 МПа. Тогда pпд.кр = 0,4pд = 4 МПа, что приблизительно соответствует глубинам 360...380 м (в зависимости от плотности жидкости и потерь давления в заколонном пространстве). Следует однако оговориться, что описанный эффект, как будет показано дальше, минимален у насадок с плавным профилем и потому нет практической необходимости вносить поправку величины mн с учетом глубины бурения.
Особенностью испытательного стенда было то, что давление на входе в стенд практически не зависело от величины противодавления (в связи с малыми расходами жидкости через стенд по сравнению с номинальной подачей центробежного насоса). В этих условиях увеличение противодавления всегда сопровождалось уменьшением перепада давления на насадке. В процессе исследования влияния противодавления на mн цилиндрических и конических насадок без скругления был обнаружен интересный факт: расход жидкости через насадку оставался постоянным, если соблюдалось условие 0 < pп*д < pп*д.кр . Иначе говоря, расход не изменялся (насадка становилась идеальным регулятором постоянства расхода, либо регулятором постоянства давления перед насадкой, если Q = const), несмотря на увеличение противодавления. Это означало, что происходящее при увеличении противодавления возрастание mн “восстанавливало” пропускную способность насадки ровно настолько, что расход Q оставался неизменным.
Параллельно с испытанием насадок в условиях наличия достаточного противодавления проводились испытания при минимальных давлениях в тупике, куда истекала струя, величины которых предопределялись гидравлическими сопротивлениями в отводном трубопроводе без штуцера (рис. 17.1). Избыточное давление в тупике (зависимости от расхода жидкости) колебалось в пределах 0,06... 0,19 МПа, а относительное абсолютное противодавление pп*д = 0,035...0,04. Строго говоря, такой вариант истечения нельзя назвать истечением в среду с атмосферным давлением, хотя (для краткости и ввиду малости pп*д) он будет называться испытанием “без противодавления”.
Экспериментальные исследования влияния относительной длины lц/dн цилиндрической насадки (рис. 17.1) на mн показали, что, если истечение через насадку происходит в условиях наличия достаточного противодавления (pп*д > pп*д.кр), то при 0 < lц / dн < 0,25 коэффициент расхода не зависит от lц/dн и всегда равен 0,62. Такие насадки обычно называют диафрагмами (рис. 17.1а) или отверстиями в тонкой стенке. В диапазоне 0,25 < lц / dн < 1,5 коэффициент mн цилиндрической насадки постепенно по криволинейному закону возрастает до предельного значения 0,82, и дальнейшее увеличение длины до 2...2,5 (получаем насадку, показанную на рис. 17.1б) не влияет на mн.
Исследования цилиндрических насадок представляют скорее методический, чем практический интерес в связи с тем, что в современных долотах они почти не применяются. Поэтому ниже излагаются результаты исследований только насадок с сужающимся каналом - “профилированных“.
Несколько замечаний по оценке точности результатов испытаний.
Расход жидкости измерялся объемным способом. Мерная емкость тарировалась весовым способом при известной температуре воды. Предельная систематическая ошибка измерения веса порции воды при тарировке - не более 0,05 %. В процессе опытов наблюдался интенсивный нагрев циркулирующей через стенд воды, поэтому постоянно, после каждого опыта, измерялась температура воды и вводилась поправка на изменение ее плотности.
Анализ показал, что предельная систематическая погрешность, обусловленная классом точности образцовых манометров, совершенством методов и приборов для измерения объема, отрезка времени и диаметра отверстий насадок, составляет не более 1 %. При этом имеется в виду тот маловероятный случай, когда знаки погрешностей всех приборов и методов измерения совпадают. Путем повторных прокачек (N=10) было установлено, что случайная ошибка определения mн существенно меньше предельной систематической. Следовательно, с весьма высокой вероятностью, близкой к 1, можно утверждать, что величины mн найдены с ошибкой не более 1 %.
В табл. 17.1 дана сводка результатов испытания насадок с различным профилем проточной части. Каждая величина mн является средней результатов не менее четырех испытаний. Обращает на себя внимание то, что в “стандартных” условиях истечения несовершенные конические насадки без скругления ничем не уступают совершенным плавным насадкам.
Таблица 17.1
Сводная таблица коэффициентов расхода коротких насадок,
используемых при бурении скважин шарошечными долотами
| Тип насадки или краткое описание профиля канала (проточной части) | Угол конуса, град(для конических. насадок) | Длина цилиндриче ского участка, м | Радиус сопряжения цилиндра с конусом, мм | Диаметр отверстия, мм | Коэффициент расхода при ис-течении в среду: | Количество испытаний | |
| без про- тиводав-ления* | с проти водавлением** | ||||||
| Эллиптическая | 15 | 10,26 10,31 | 0,974 | 1,022 | 4 ´ 4 | ||
| Радиальная | 7 | 10,26 10,31 | 0,971 | 1,031 | 2 ´ 5 | ||
| Бирадиаль-ная (конои-дальная) | 3 | 10,26 10,31 | 0,956 | 1,017 | 3 ´ 6 | ||
| Профиль естественного износа | 2,5 | 10,26 10,31 | 0,916 | 1,002 | 3 ´ 4 | ||
| Коническая | 14 | 6 | 0 | 10,26 10,31 | 0,957 | 0,997 | 4 ´ 3 |
| Коническая | 37 | 6...8,5 | 0 | 10,26 10,31 | 0,874 | 1,024 | 4 ´ 6 |
| Коническая | 75 | 4,5 | 0 | 10,26 10,31 | 0,782 | 0,957 | 2 ´ 2 |
| Коническая | 75 | 4,5 | 3...4 | 10,26 10,31 | 0,926 | 0,993 | 4 ´ 6 |
| Удлиненная керамичес-кая | 10,64 10,7 | 0,98 | 1,008 | 3 ´ 4 | |||
| Короткая керамическая | 9,9 | 0,976 | 1,006 | 2 ´ 2 | |||
*) относительное противодавление среды не более 0,04;
**) относительное противодавление среды не менее 0,62
В начале данного раздела было показано, что mн может быть больше 1, если присутствует противодавление и величина восстановленного давления (части кинетической энергии потока) больше потерь давления в насадке на этапе разгона потока. Факты совпадения величин mн с известными из литературы в условиях истечения в среду без противодавления, а также отсутствие влияния противодавления при отсутствии цилиндрического спрыска и многократная проверка полученных результатов, свидетельствуют о том, что превышение mн единицы в условиях достаточного противодавления не является результатом ошибки опытного определения искомой величины.
Этот факт объясняется тем, что в условиях истечения в тупик создаются условия для частичного превращения скоростного напора струи в давление. Не исключено, что этому явлению способствует стесненность пространства для струи и наличие возвратного потока. Отсутствие влияния противодавления при lц = 0 объяснятся неравномерностью распределения скорости по сечению внутри насадки и ее сжатием за пределами насадки. Цилиндрический участок выравнивает скорость потока по сечению, что подготавливает условия для проявления эффекта указанного частичного превращения кинетической энергии струи в давление среды. При истечении струи в спутный поток или в тупик больших размеров (относительно диаметра отверстия насадки) такого эффекта может не быть. Он может не проявиться и в реальном долоте вследствие больших относительных размеров пространства и отсутствием соизмеримых с расходом струи возвратных потоков, как это имело место в экспериментальной установке с единичной насадкой.
Специальные испытания реальных долот полностью подтвердили сказанное: ни в одном из опытов коэффициент расхода промывочной системы долота в целом не оказался больше 1.
Основываясь на опытных данных и учитывая то обстоятельство, что давления в скважине, начиная с глубин 350...500 м, заведомо превышают критические, при применении в гидромониторных долотах насадок с плавным профилем (бирадиальных, радиальных), имеющих цилиндрический участок длиной (0,5...1,0), для практических расчетов можно рекомендовать mн =0,990...0,985.
Результаты испытания насадки с “профилем естественного износа” дают веские основания для рекомендации уменьшить длину ныне применяемой стандартной насадки с бирадиальным профилем на 3...4 мм, что даст существенную экономию твердосплавного материала.
Знание точных значений mн является важнейшим условием более точного определения коэффициента расхода промывочной системы долота mд , а через него - pд по формуле
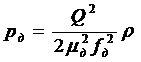 .
.
Коэффициент расхода отдельно взятого промывочного канала mпк зависит от mп , mн и соотношения диаметров dн и dп. Впервые на это указал А.К. Козодой, предложивший формулу, которую можно преобразовать к виду:
 , (17.6)
, (17.6)
где b* = dн/dп - коэффициент раскрытия насадки (по А.К. Козодою).
Для определения mп были поставлены специальные опыты с серийным долотом без насадок, которые показали, что mп = 0,7. Однако надо учитывать, что наличие насадки делает входной участок подобным цилиндрической насадке, поэтому логично принимать mп = 0,82.
Если заменить mн и mп на их экспериментально найденные значения (соответственно 0,985 и 0,82), то получим формулу:
 . (17.7)
. (17.7)
При промывке с применением равноразмерных насадок mд = mпк.
Коэффициент расхода промывочной системы долота mд (для краткости в дальнейшем: “коэффициент расхода долота”) при использовании разноразмерных насадок определяется по формуле, полученной из условия постоянства перепада давления на долоте:
 , (17.8)
, (17.8)
где z - число используемых насадок,
i - порядковый номер насадки.
Расход жидкости через насадку Qi и скорость истечения vи.i вычисляются по формулам:
 , (17.9)
, (17.9)
 . (17.10)
. (17.10)
При разноразмерных насадках mпк будет меньше там, где больше dн.i. Следовательно, при dп = const скорость истечения будет меньше там, где больше диаметр насадки.
Использование насадок большего диаметра (при dп = const), как это следует из формулы (17.7), означает увеличение потребного перепада давления на долоте для обеспечения запланированной скорости истечения. В “идеале” для создания струи, например, с гидродинамичесим давлением в 10 МПа достаточно иметь 10/mн2 = 10/ 0,9852 = 10,31 МПа исходной потенциальной энергии давления, но для того, чтобы приблизиться к этому “идеалу” необходимо, чтобы коэффициент раскрытия b* былне более 0,25.
17.1.3. Исследование распространения затопленных струй
и их динамического воздействия на забой скважины.
Прежде чем приступить к изложению результатов экспериментального исследования струй, истекающих из модельных и реальных насадок долот, рассмотрим вопросы методики расчета параметров затопленных струй и обработки опытных данных.
А.К. Козодой доказал, что зависимость гидродинамического давления струи по ее оси pос от относительного расстояния m текущего ее сечения до насадки, измеренного в диаметрах отверстия насадки, обеспечивает достаточно полную количественную характеристику струи, поскольку все другие ее характеристики (форма внешней границы струи, распределение скорости потока в сечении и гидродинамического давления) однозначно зависят от функции pос(m).
А.К. Козодой предложил упрощенную модель распространения затопленной струи, которая сводится к тому, что граница струи представляет собой коническую поверхность, в том числе и в пределах начального участка. Совместив эту схему с известным положением о постоянстве количества движения по сечениям струи, он получил широко используемые формулы для определения диаметра струи d и гидродинамического давления по ее оси pос (рис. 17.4):
 , (17.11)
, (17.11)
m = lс / do ,
pо = lpo , (17.12)
 , (17.13)
, (17.13)
 , (17.14)
, (17.14)
mo = lo / dн ,
где d - текущий диаметр струи;
l - относительная величина осевого гидродинамического давления струи (сокращенно в дальнейшем изложении: “относительное осевое давление струи”);
vo - средняя начальная скорость струи на выходе из насадки;
lo, lс - соответственно расстояния до начального и текущего (на основном участке) сечений струи;
a - коэффициент расширения струи;
mo - относительная длина ядра струи;
m - безразмерное (относительное) расстояние от насадки;
r - плотность жидкости.
Параметр mo оказался очень удобным для оценки гидродинамического совершенства насадок с точки зрения влияния конструкции насадок на свойства струи. Вместе с тем предложенная А.К. Козодоем расчетная схема, основанная на постоянстве коэффициента a по длине струи, при истечении струи в тупик дает существенные расхождения с опытом (в сторону завышения), причем именно на тех расстояниях, которые типичны для практики бурения (более 8...10 диаметров насадки). При m > 13...15 ошибка может быть кратной.
 П.Ф. Осипов предложил [3] несколько “модернизировать“ предложенную А.К. Козодоем расчетную схему, заменив, по существу, постоянный коэффициент a на функцию, зависящую от параметров m и mo:
П.Ф. Осипов предложил [3] несколько “модернизировать“ предложенную А.К. Козодоем расчетную схему, заменив, по существу, постоянный коэффициент a на функцию, зависящую от параметров m и mo:
a = ao +b(m - mo), (17.15),
где ao - угловой коэффициент в переходном сечении, в котором d=dпх, а m=mo;
b - показатель отклонения границы струи от прямолинейной.
Тогда формулу (17.11) можно заменить зависимостью:
d = do{1+ [ao +b(m - mo)]m}. (17.16)
Коэффициент b в дальнейшем будем называть “показателем интенсивности массообмена” или “показателем массообмена” на основном участке струи. Чем больше b, тем интенсивнее расширяется струя, тем интенсивнее проходит массообмен со средой, тем больше отличается образующая границы струи на основном участке от прямой, а струя - от конуса. С другой стороны, константа ao больше характеризует влияние условий формирования струи внутри насадки на ее распространение вне ее.
Важнейшим в практическом отношении показателем является коэффициент l - относительное осевое давление струи.
Из условия постоянства количества движения в любом сечении основного участка затопленной струи следует известное соотношение l = (dп/d)2 . Тогда формула для l (17.14) примет вид:
 . (17.17)
. (17.17)
Коэффициент ao непосредственно характеризует расширение струи на начальном участке, а на параметры струи на основном участке влияет лишь косвенно (через диаметр струи в переходном сечении, где a = ao ).
А.К. Козодой экспериментально доказал, что amo = 1,34. Следовательно, в переходном сечении, где a = ao; amo = aomo = 1,34 и ao = 1,34/mo. Тогда получаем новую формулу для l :
 . (17.18)
. (17.18)
Экспериментально установлено, что при истечении струй из насадок с плавным профилем (независимо от вариантов оформления профиля проточной части) mo = 6, а b = 0, 01. Тогда формула (17.18) преобразуется к виду:
 . (17.19)
. (17.19)
На срезе насадки (в выходном сечении при lc=0) расход струи равен Qo – подаче насосов. По мере удаления от насадки расход струи увеличивается за счёт присоединённой массы жидкости извне (рис. 17.4). Такое возможно только в том случае, если основная масса жидкости находится в постоянной циркуляции, многократно попадая в струю и выходя из неё после удара о забой. Поэтому представляется вполне естественным, когда выбуренная порода вновь и вновь попадает в струю и “загоняется” в зону разрушения забоя долотом, подвергаясь дополнительному измельчению. Установленно, что текущий расход равен:
Q = Qo {1+[ ao +b(m - mo) m]} (17.20)
Эта формула заслуживает специального анализа. Выражение в фигурных скобках, как показывают расчёты, существенно больше единицы. Длина струи lc у долот диаметром 215,9 мм – около 150 мм. Предположим, что dо=12 мм. Тогда m=150/12=12,5, а величина в фигурных скобках 1 + [0,223+0,01(12,5-6)]12,5 = 4,6. Это означает, что перед встречей с забоем расход струи более чем в 4 раза превышает начальный расход Qо. Итак, на уровне насадки равен Qо, а на забое - 4,6Qо.
Кинетическая энергия (усреднённая по сечению) струи вычисляется по формуле:
Е=Ео /{1+[ao +b(m - mo) m]} (17. 21)
До сих пор мы говорили, в основном, об изменении гидродинамических параметров по оси струи. Но скорость в струе и, как следствие, гидродинамическое давление различны на разных расстояниях y от оси (рис. 17.4). Эксперименты показали, что изменение скорости vy от текущего радиуса y можно удовлетворительно писать уравнением:
 (17.22)
(17.22)
а гидродинамическое давление:
 (17.22)
(17.22)
На рис. 17.4 показана эпюра рy. На границе струи vу и pу принимаются равными нулю (что равноценно признанию, что продольная составляющая скорости на границе равна нулю, но при этом поперечная составляющая больше нуля, так как имеется приток жидкости извне как результат инжекции). В центре струи (на оси) vo=vос, pу=pос.
17.2. Фильтрационные потоки в разрушаемой породе,
возникающие при воздействии на нее подвижной
гидромониторной струи.
Впервые фильтрацию жидкости под воздействием подвижной (перемещающейся) струи исследовали П.Ф. Осипов и В.И. Зелепукин.
При отсутствии вращения долота фильтрация жидкости в “пятне поражения” забоя гидромониторной струей осуществляется под действием дифференциального давления pдиф (репрессии) и ударного давления струи pуд, величина которого зависит от характеристики “волны” давления. В пределах пятна жидкость фильтруется только в сторону породы (прямая фильтрация), а в кольцевой зоне, непосредственно примыкающей к пятну поражения снаружи, образуются, как показал Ю.И. Коваленко, фильтрационные потоки, направленные в сторону скважины. Такие потоки можно назвать “обратными”. Последние способствуют отрыву частиц породы от забоя или, при благоприятных условиях, даже его разрушению.
Вращение гидромониторного долота вносит существенные изменения в картину фильтрационных потоков на забое скважины. Вызванные действиями струй волны давления (рис. 17.5), двигаясь вдоль забоя по окружности, приводят к тому, что на любой площадке забоя, оказавшейся в зоне их действия (в кольцевой полосе поражения), действующее на забой давление pзаб становится величиной переменной во времени и меняется от pс до pс + pуд , а затем снова уменьшается до pс. Воздействие носит импульсный характер с паузами между импульсами (количество импульсов за один оборот равно числу установленных в долоте насадок), причем продолжительность пауз, как правило, больше продолжительности воздействия.

Рис. 17.5. Изменение избыточного (над пластовым) давления на окружности, описываемой на забое скважины центрами гидромониторных струй, в зависимости от угла поворота долота (в долях от полного оборота): n =60 мин-1, dн = 10 мм, lc = 150 мм.
Из полосы воздействия выберем узкую полосу, центр которой расположен на линии, описываемой точкой пересечения оси струи с забоем скважины на радиусе Rc,где ударное давление pуд равно гидродинамическому давлению в центре струи. Упростим задачу предположив, что струя создает не осесимметричную, а симметричную относительно вертикальной плоскости волну давления. Ширину волны (вдоль радиуса скважины) примем равной диаметру струи, что позволит (в первом приближении) пренебречь влиянием крайних участков “полосы поражения” (на радиусах Rc+d/2 и Rc-d/2) на результаты расчетов на радиусе Rc. В итоге задача из трехмерной (с переменными вдоль радиуса параметрами волны давления) в плоскую, и процесс фильтации вязкой жидкости в породу может быть описан известным уравнением плоско-параллельной фильтрации упругой жидкости в упругой среде, называемым уравнением пьезопроводности:
 , (17.22)
, (17.22)
где p - давление в массиве породы на некотором расстоянии x от забоя,
k = kп/mbу - коэффициент пьезопроводности,
kп - проницаемость породы,
m - динамическая вязкость жидкости,
bу = bжmп + bп - коэффициент упругоемкости породы,
mп - пористость породы,
bж , bп - коэффициенты сжимаемости (коэффициенты объемной упругости) соответственно жидкости и породы.
Предположим, что бурение породы осуществляется со скоростью, когда на забое не успевает сформироваться градиентный слой, и давление на всем полупространстве массива породы равно пластовому. Допустим, что, не прерывая вращения долота, прекращена подача инструмента, прервано углубление скважины. Этот момент примем за начало отсчета времени (t = 0). Условимся, что при t = 0 “точка наблюдения”, расположенная на окружности с радиусом Rc, находится под шарошкой долота и действующее на нее давление равно pзаб = pc = pпл + pдиф , как показано на рис 17.5.
На основе изложенного можно определиться с начальными и граничными условиями для решения уравнения (17.22):
p(x,t) = pпл при t =0; (17.23)
p(x,t) = pзаб (t) при x = 0 и t >0, (17.24)
p(x,t) = pпл при x = ¥ , t ³ 0. (17.25)
Скорость фильтрации определяем согласно закону Дарси:
 . (17.26)
. (17.26)
Эпюра ударных гидродинамических давлений на забой в сечении основного участка струи описывается зависимостью
 , (17.27)
, (17.27)
где y - расстояние от оси струи (если ось x совпадает с осью струи);
r - радиус струи в избранном сечении;
bc - коэффициент, управляющий интенсивностью изменения давления при
0 < y < r; выше было показано, что bc для затопленной струи, истекающей в тупик равно 3,5.
pос - гидродинамическое давление на оси струи, величина которого зависит от расхода жидкости, диаметра насадок, расстояния до забоя и др.
На рис. 17.5 показан график изменения ударного давления в зависимости от угла поворота долота.
За время, в течение которого центр (вершина) 1-й волны давления оказывается над точкой наблюдения, долото сделает 1/ 6 оборота, а центр струи пройдет путь 2pRc(1/6) . В общем случае, через некоторое время t , когда центр струи пройдет расстояние 2pRc(nt)на забое будет давление pзаб = pпл + pдиф + pуд.t . Величина последнего слагаемого определяется текущей координатой y, равной:
y = 2pRc(nt) - 2pRc(1/6) = 2pRc(nt - 1/6).
В зависимости от t (при выбранном n) величина y может быть и отрицательной (фаза нагнетания) и положительной (фаза падения давления).
Еще через 1/3 оборота, при nt = 0,5, над изучаемой площадкой окажется вершина второй волны и т. д. Вычисление параметров волны давления в окрестностях вершины волны осуществляется по тому же алгоритму.
Из сказанного можно заключить, что граничное условие (17.24) может быть записано в виде
pзаб = rgl + pуд , (17.28)
 , (17.29)
, (17.29)
где pос - гидродинамическое давление струина расстоянии от насадки, соответствущем забою;
n - скорость вращения долота, с-1;
r - радиус струи;
r - плотность жидкости;
l - глубина скважины;
N - порядковый номер очередной волны давления.
Формула (17.29) предназначена для определения параметров волны давления, и предполагает, что ее применению предшествует идентификация номера очередной волны давления, ее стороны (передней или тыльной) и определение границ между действиями струй (пауз), когда pуд =0.
При численном решении уравнения (17.22) на ПЭВМ функция (17.29) задается в табулированном виде для любой продолжительности и любого заданного шага по времени, продиктованного желаемой точностью расчета.
Правомерность применения вязкой жидкости (в численном эксперименте - воды) в качестве фильтрующейся жидкости и уравнения (17.22) при указанных начальных и граничных условиях основывается на следующем:
1) проницаемость образующейся на забое в процессе бурения глинистой корки несоизмеримо велика по сравнению с проницаемостью породы в связи с тем, что забой постоянно обновляется и происходит удаление корки вместе с породой и смыв ее отраженной от забоя струей; иначе говоря, влиянием корки на процесс фильтрации можно пренебречь;
2) пластовая жидкость и фильтрат бурового раствора в основном представлены водными растворами солей, вязкости которых можно принимать практически равными и рассматривать их как одну жидкость;
3) физико-химическим взаимодействием жидкости с горной породой в процессе фильтрации можно пренебречь.
П.Ф. Осиповым, В.И. Зелепукиным и Ю.Л. Логачевым для решения уравнения (17.22) разработана специальная компьютерная программа, в которой использованы известные методы численного решения уравнений параболического типа. Программа предоставляет пользователю возможность:
- получать графики изменения давления и скорости фильтрации в массиве породы на расстоянии до 0,25 м;
- проследить за изменением параметров фильтрации для любого интервала времени с любой частотой фиксации промежуточных “кадров”;
- задавать любые параметры струи (как симметричные, так и асимметричные) и скорости вращения долота.
С использованием программы проведены численные эксперименты с целью установления или уточнения влияния различных факторов на фильтрацию жидкости в породе.
Расчеты показали, что под воздействием струи в массиве породы, прилегающем непосредственно к забою, изменяется не только давление, но и скорость, и направление фильтрации. С технологической точки зрения интерес представляют скорости и градиенты давления на расстоянии не более 10-15 мм от плоскости забоя, поскольку именно такие размеры имеет зона предразрушения, где формируется система трещин при работе шарошечного долота. Анализ показал, что критерием оценки фильтрационной картины в любой момент времени должна быть скорость фильтрации через поверхность забоя vф. Влияние же того или иного фактора промывки на процесс очистки или разрушение забоя следует оценивать на основе зависимости vф от поворота долота j = nt.
На рис. 17.6 показан пример зависимости vф(j), начиная с момента начала воздействия 3-й струи (j = 0,78), до “прихода” четвертой. Для удобства направление фильтрации в сторону породы принято за отрицательное (вниз), а в сторону скважины - за положительное (вверх). Видно, что после прохождения центра струи (тыльная сторона волны давления) происходит резкое, почти ударное, изменение направления фильтрации на положительное, возникает обратная фильтрация, которая продолжается, затухая относительно медленно, даже после “ухода” струи. К моменту “прихода” в точку наблюдения движущейся следом за струей шарошки (j = 1) фильтрация снова становится отрицательной, правда, при уменьшенном значении призабойной репрессии (скорость фильтрации явно меньше скорости фоновой фильтрации в промежутке между импульсами). На рис. 17.6, кроме того, приведен график изменения толщины депрессионного слоя. В данном конкретном случае максимальная толщина этого слоя достигает 16 мм, причем в момент, когда vф максимально, она не превышает 10 мм.
На рис. 17.7 показан пример промежуточного “кадра” фильтрации, соответствующего моменту достижения максимума скорости обратной (положительной) фильтрации.
Из примера расчета (рис. 17.7) можно заключить, что зависимость vф(j) дает возможность получить четкое представление о фильтрационных процессах, происходящих на забое скважины под влиянием подвижных гидромониторных струй.
График на рис. 17.7 получен при перепаде давления pд = 11,4 МПа, диаметре насадок dнас = 10,2 мм, плотности бурового раствора 1150 кг/м3 , при pдиф =3,2 МПа и расстоянии от насадки до забоя lс = 120 мм. Коэффициент пьезопроводности k = 0,01 м2/с. Эти перечисленные условия примерно соответствуют случаю бурения на глубине 3000 м при индексе пластового давления не более 1,05, что типично, например, для многих площадей Урало-Поволжья и Республики Коми.
Вызываемая струей фильтрация на забое, как будет показано в дальнейшем, хорошо объясняет особенности и противоречия в результатах применения гидромониторных долот, в частности, парадоксальную обратную зависимость между приростом механической скорости от струйной промывки и стойкостью долот. С точки зрения поиска путей более эффективного применения шарошечных гидромониторных долот необходимо определить основные факторы, влияние которых имеет практическое значение, и дать количественную оценку их влиянию.
В следующих подразделах приведены результаты исследования влияния технологических (перепада давления на долоте, скорости его вращения, дифференциального давления), технических (приближения насадок к забою, применения насадок, формирующих асимметричные струи, или специальных средств для создания кавитации) на интенсивность и продолжительность фильтрации.

Рис. 17.6. Изменение скорости и направления фильтрации жидкости через плоскость забоя при вращении долота ( Pдол=11,4 МПа; dнас=10,2 мм; L=3000 м; n = 1 с-1; Q = 22 л/с ):
1 - скорость фильтрации;
2 - толщина депрессионного слоя
Дата добавления: 2018-06-27; просмотров: 921; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
