Совмещение гидравлических характеристик скважины и насосов.
На рис. 12.4. показаны гидравлические характеристики скважины (линии 1,2,3) и насосных агрегатов (одного насоса – линия 4; двух насосов – линия 5).
Линия "р – Q" (линия 3) пересекает гидравлические характеристики насосных агрегатов, представленных, например, пятью вариантами диаметров втулок, в точках М и N . Это означает, что подачи Q1н и Q2нявляются для скважины пpeдeльнo доcтижими. Проще говоря, имея данные насосные агрегаты, через данную конкретную скважину невозможно прокачивать жидкость с расходом, превышающим соответственно Q1н и Q2н .Следовательно, реальная область регулирования подачи находится левее указанных расходов.
12.4. Решение задачи совмещения гидравлических
характеристик скважины и насосов с учетом
технических и технологических ограничений
Кроме точек М и N , ограничивающих расход Q справа, существует ряд технических и технологических ограничений:
1. Общее ограничение на давление на буровой рдоп. На рис. 12.4 это соответствует расходу Qдоп . Это ограничение может "сработать" только при двух насосах.
- Минимально технологически необходимый расход Qmin .
Величина Qmin определяется необходимостью очистки ствола и забоя скважины или другими технологическими факторами. Этот расход ограничивает слева реальную область регулирования (выбора) расхода Q .
- Допустимые потери давления в заколонном пространстве.
Причины, побуждающие к такому ограничению, весьма серьезны. Это и предупреждение загрязнения продуктивного пласта, сохранение буримости (уменьшение дифференциального давления), предупреждение поглощения бурового раствора.
|
|
|

Рис. 12.4. Совмещение гидравлических характеристик насосов
и скважины.
Предположим, что допустимые потери давления равны рк.доп. Тогда предельно допустимым расходом является Qк.доп . Точка R находится правее всех характерных точек M и N. Это означает, что рк.доп фактически снимает всякое ограничение на Q, поскольку величина рк.доп задано чрезмерно большой.
Предположим теперь, что ограничение на потери в кольцевом пространстве уменьшено до величины р’к.доп . Тогда получится, что расход необходимо ограничивать величиной Q’к.доп . В итоге придется смириться с тем, что при учете всех трех вышеперечисленных ограничений доступная область регулирования (выбора) сузится до интервала от Qmin до Q'к.доп .
Вопросы рационального использования гидравлической мощности насосов.
Предположим, что сочетание гидравлических характеристик скважины и насосов отражается полностью на рис. 12.4. Предположим, что привод электрический (жесткий), а возможность регулирования ограничена пятью диаметрами цилиндровых втулок насосов (варианты I - V с подачами от Q1 до Q5 ).
|
|
|
Если все ограничения на выбор Q предопределены величинами Qmin и Q’к.доп, то получается, что нет никакого смысла использовать второй насос, поскольку любой расход в указанных пределах может быть обеспечен только при работе одного насоса, причем выбор ограничен только одним вариантом - втулками II с расходом Q2 . Если бы привод был дизельным, то, вероятно, тот же расход Q2 мог бы быть обеспечен втулками III в сочетании с уменьшением числа ходов насоса.
Итак, при электроприводе выбор останавливаем на единственно возможном варианте Q2. Насос мог бы создать давление р2, но здесь вспомним, что на буровой действует общее ограничение давления до величины рдоп< р2. При расходе Q2 на насосе будет давление, соответствующее точке "а" (таково рн при Q2 по гидравлической характеристике скважины). Но ра < рдоп. Имеет место, следовательно, явное недоиспользование мощности и давления. При роторном бурении следует уменьшить сечение отверстий гидромониторных насадок так, чтобы перепад давления на долоте был равен отрезку "ав":
рд =рдоп – рп.
При турбинном бурении следует заменить турбобур на забойный двигатель, обеспечивающий увеличение перепада давления. Например, добавить одну или две новые секции турбобура.
|
|
|
Предположим, что ограничение р’к.доп снято и есть возможность увеличить Q. Реально в этом случае применение варианта втулок III (расход Q3 при предельном давлении р3), потому что следующий вариант IV находится в недоступной области, правее точки М. Тогда резерв давления для долота (или турбобура) будет равен отрезку с’-III, а недоиспользованная часть давления – отрезку а’ – III. Иначе говоря, вместо ограничения рдоп здесь следует использовать р3.
Обращаем внимание на следующее обстоятельство. Если заменить насадки (с целью увеличения давления) или добавить секции турбобура, то линия 3 будет другой, а вот линия 2 останется на прежнем месте. Изменения коснутся только линии 3, потому что увеличатся перепады на долоте или турбобуре (отрезки са или с'а') при сохранении, повторяем, потерь давления (линии 2). При Q =Q2 новая линия 3 непременно должна пройти через точку "в", а при Q=Q3 – через точку III.
13. Расчет параметров промывки скважины и режима работы
буровых насосов.
13.1. Упрощенная методика пересчета параметров промывки
при изменении подачи насосов.
Вязкопластичные жидкости.
|
|
|
Вспомним, что существуют точные методы расчета потерь давления при структурном движении в трубном и в заколонном пространствах. Для трубы точным методом является уравнение Букингэма или предложенный Гродде метод решения этого уравнения. Формула Бингама по сравнению с упомянутыми методами расчета является приближенной, менее точной (как результат "отбрасывания" третьего члена в уравнение Букингэма). Если обозначить в (5.2):
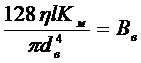 ,
,
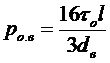 ,
,
то уравнение Бингама для трубного пространства будет иметь вид:
рв =ро.в+Вв Q. (13.1)
Аналогично для заколонного пространства:
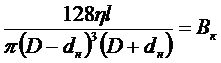 ,
,
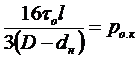 .
.
Тогда
рк =Ро.к +ВкQ . (13.2)
Величины ро.к , ро.к ,Вв ,Вк не зависят от Q , поэтому, если их знать, то пересчет рв или рк на новое значение Q не представляет никаких трудностей.
В практике расчетов возникает часто ситуация, когда известна, например, величина рв1, соответствующая некоторому известному Q1, причем Q1 < Qкр. Чтобы получить для пересчета давлений уравнение типа (13.1), необходимо рассчитать величину ро.в. Тогда Вв найдется по формуле:
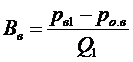 . (13.3)
. (13.3)
Аналогично для кольцевого пространства:
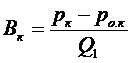 . (13.4)
. (13.4)
Для долота, турбобура и манифольда потери (или перепады) давления определяются по единообразной формуле:
р =АrQ2, (13.5)
и пересчет давлений для этих элементов не сопровождается новыми погрешностями, превышающими погрешность формул. Сложнее обстоит дело с турбулентным режимом течения в доквадратичной (переходной) области, когда в формуле Дарси-Вейcбаха l зависит от Q . Для ускорения пересчета рв или рк, на новое значение приходится принимать допущение (предположение): если рв1 или рк2 при Q = Q1 найдены "строгим" путем, с учетом влияния Q на l , иначе говоря, с использованием формулы (6.9), то условно считается (принимается), что в окрестностях рв1 или рк2 существует квадратичная (параболическая) зависимость рв или рк от Q . Разумеется, такое допущение будет искажать результат пересчета с плюсовой ошибкой (завышать), когда Q2 > Q1, и занижать, когда Q2<Q1. Ошибка будет тем меньше, чем ближе Q к Q1 . И напротив, ошибка рв2 или рк2 будет возрастать, когда Q "удаляется" от Q1.
Обобщим изложенное. Проследим за изменением вида зависимости рн =f(Q) по мере увеличения Q от малых значений до больших, соответствующих квадратичной области. Если в скважине только трубы и расход таков, что везде структурный режим, то
рн=ро +(Вв+Вк)Q . (13.6)
Если учесть потери давления в манифольде, турбобуре и долоте, то
рн=ро.в+ро.к+(Bв+Bк)Q+(Aобв+Атрб+Ад)rQ2 . (13.7)
Если приступить теперь к увеличению Q , то в одном из элементов циркуляционной системы (скорее всего в трубах) наступит турбулентный режим, что приведет к тому, что уравнение (13.7) видоизменится:
рн= ро.к+ВкQ +(Aобв+Атрб+Ад+Ав)rQ2 . (13.8)
Если и в заколонном пространстве исчезнет структурный режим, то наступит ситуация:
рн= (Aобв+Атрб+Ад+Ав+Ак)rQ2 , (13.9)
что равноценно формуле (13.5).
В этом уравнении источником погрешности являются Ав и Ак, потому что в переходной области турбулентного течения они не могут считаться постоянными, поскольку:
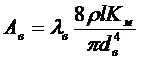 , (13.10)
, (13.10)
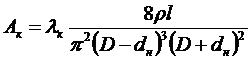 , (13.11)
, (13.11)
где lв и lк являются функциями Re* и Sen.
На практике часто возникает ситуация, когда нужно определить А для составления уравнений типа (13.5). Для этого необходимо определить "строгими" методами р, заведомо зная, что при выбранном Qрасч режим движения турбулентный, а затем найти искомое значение А:
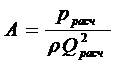 . (13.12)
. (13.12)
В практике расчетов часто приходится определять Q, при котором давление на насосах, например, когда оно равно некоторому наперед заданному значению (обратная задача). Предположим, что рн ограничивается величиной рдоп. Если потери давления описываются уравнением (13.6), то искомый расход Q равен:
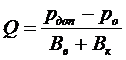 . (13.13)
. (13.13)
Если функция рн =f(Q) описывается уравнением (13.5), то
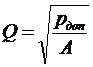 . (13.14)
. (13.14)
Таким образом, при "чисто" структурном или "чисто" турбулентном режимах движения определение искомого Q выполняется достаточно просто.
Сложнее обстоит дело, когда зависимости рн =f(Q) описываются уравнениями (13.7) или (13.8), когда приходится, строго говоря, искать корень полного квадратного уравнения. В таких случаях обычно прибегают к следующему допущению. Обычно сравнивают потери (или перепады) давления, относящиеся к турбулентному режиму движения, с суммой потерь давления на тех участках, где режим движения был структурным. Допущение заключается в том, что пренебрегается одной из этих сравниваемых величин. Если, например, "структурные" потери давления окажутся меньше "турбулентных", то все потери (перепады) условно относятся к турбулентным, а зависимость рн =f(Q) относят к виду (13.5). В противном случае – к виду (13.2).
Псевдопластичная жидкость.
Строгие методики расчетов потерь давления описаны в разделах 7 и 8.
Если в одном из элементов в трубах имеет место ламинарный режим движения, то потери давления удобнее рассчитывать по формуле:
р =SвQn , (13.15)
где
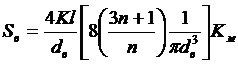 . (13.16)
. (13.16)
Если решать обратную задачу, то искомый расход определяют по формуле:
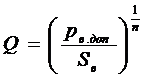 . (13.17)
. (13.17)
Аналогичным образом решается задача и для затрубного пространства.
При турбулентном течении расчетную формулу можно представить в виде:
р =ТQ1,8 , (13.18)
где
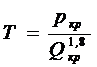 . (13.19)
. (13.19)
Обратная задача решается по формуле:
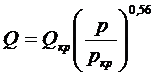 . (13.20)
. (13.20)
Дата добавления: 2018-06-27; просмотров: 628; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
