Постановка задачи. Вывод уравнения скорости спутного потока.

Попытки строго теоретического решения задачи выглядят не очень убедительными, прежде всего, по причине неустойчивости во времени эпюры скоростей, о чем говорилось выше. С другой стороны, не вызывает у практиков вдохновения громоздкость решений, требующих применения вспомогательных таблиц и т.п. и потому трудно реализуемые даже на ЭВМ.

В практике расчетов гидродинамического давления p_гд или допустимых скоростей u_доп спуска (подъема) колонн предпочтение (и вполне заслуженное) отдается методике, предложенной впервые Ормсби [3] и базирующейся на использовании принципа суперпозиции и понятия эквивалентной скорости. Принимается, что суммарный эффект влияния Q_ск и Q_вт “эквивалентен” потерям давления при промывке скважины с эквивалентной скоростью v_экв , определяемой по формуле:

v_экв = u_т K_ск + u_т d_н²/(D² – d_н²).                            (14.3)

Перейдем к эквивалентному расходу:

Q_экв = v_экв p (D² - d_н²)/ 4;                                       (14.4)

Q_экв = u_т K_ск p (D² - d_н²)/ 4 + u_тpd_н²/4.                     (14.5)

Первое слагаемое в уравнении - это отражение влияния Q_ск на p_гд, а второе – численно равно Q_вт.

Чтобы найти p_гд для заданной скорости движения u_т в случае движения одноразмерной колонны, достаточно расход Q_экв  считать расходом промывки Q через заданную колонну в той же скважине и, пользуясь известными методиками и формулами для промывки, найти потери давления в затрубном пространстве. Эти потери и будут численно равны искомому гидродинамическому давлению при спуске колонны (с положительным знаком) или при ее подъеме (с обратным знаком).

В методике, основанной на понятии эквивалентной скорости, основным моментом является вопрос определения коэффициента K_ск. По физическому смыслу K_ск - это отношение расхода Q_ск к некоторому условному расходу Q_пол=u_т f_кп, исходя из предположения, что весь объем жидкости в заколонном пространстве с сечением f_к движется вместе с колонной с одной и той же скоростью u_т:

K_ск = Q_ск / Q_пол.                                              (14.6)

Как видим, Q_экв равен сумме Q_ск  и Q_вт , хотя эти расходы противоположны по направлению. Такой подход не может считаться теоретически строгим, но он с лихвой возмещается простотой и вполне удовлетворительной сходимостью с опытом. Кроме того, геометрические размеры скважины отличаются большой неопределенностью, что делает бессмысленным применение “сверхстрогих” методик расчета.

Для привычных сочетаний диаметров скважины и бурильных труб при бурении основного ствола в литературе [2, 3] рекомендуется принимать K_ск = 0,45...0,50, причем большие значения соответствуют малым зазорам между трубами и скважиной.

Учитывая, что в практике бурения соотношение диаметров труб d_н и скважины D колеблется в широких пределах, в особенности при бурении под промежуточные колонны, попытаемся получить выражения для K_ск=f(d_н,D), что позволит существенно повысить точность расчетов гидродинамических давлений и допустимых скоростей движения колонн труб.

Бурильные колонны, как правило, разноразмерны по наружному диаметру труб d_н.

Рис. 14.4. Спуск в скважину двухразмерной колонны.

На рис. 14.4 показан случай спуска “закрытой” колонны с диаметрами секций труб d₁и d₂. Из формулы (14.5) следует, что для каждой секции будут свои значения Q_ск и Q_вт. Следовательно, в отличие от промывки скважины, когда для любой секции Q=const, расчет р_гд ведется при различных значениях Q_ск, Q_вт и  Q_экв . Из сказанного также следует, что получение зависимости K_ск=f(d, D) является актуальной задачей.

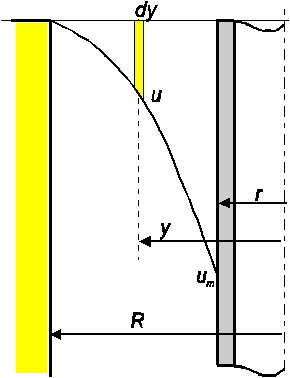
Вначале установим зависимость напряжений в жидкости t  от радиуса r (рис. 14.5). Для поддержания равномерного движения колонны к ней нужно приложить некоторое усилие G (частичная разгрузка веса). Оно должно быть равно силе сопротивления на поверхности колонны труб длиной l. Если на стенке труб касательные напряжения обозначить через t_r, то

G = 2p rlt_r .

Из условия динамического равновесия следует (рис. 14.5), что

G = 2p ylt.

Тогда

2p rlt_r = 2p ylt,

t = rt_r /y .                                                    (14.7)

Как видим, зависимость t(y) имеет гиперболический характер. (Кстати, напомним, что подобная зависимость для трубы линейна).

При y = R t = t_r.

Тогда

t_R =t_r r /R .                                                         (14.8)

Для любой жидкости очевидна реологическая функция:

du/dy = -j(t);

du = -j(t) dy.                                  (14.9)

Из соотношения (14.7) после дифференцирования:

dy = - t_r r(dt/t²).

Подставив в (14.9), получим:

.

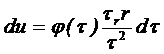После интегрирования в пределах от u до 0 и от t до t_R имеем:

.                  (14.10)

Это уравнение для спутного потока справедливо для любых жидкостей с известной реологической функцией j(t). Оно не учитывает влияния вытесняемого потока на эпюру скоростей.

14.2.2. Расчет коэффициента К_ск для случая, когда в скважине вязкая жидкость.

Найдем конкретное выражение для скорости жидкости в кольцевом пространстве для вязкой жидкости с реологическим уравнением

j(t)=t /m,                                             (14.11)

которую подставим в (14.10):

.  (14.12)

Интегрирование дает результат:

.   (14.13)

Из (14.8) следует, что t_R/t = y/R и t_R/t_r = r/R . Учитывая, что на стенке трубы u = u_т , а на стенке скважины u = 0, получаем зависимость u(y):

. (14.14)

Чтобы найти Q_ск , нужно просуммировать расходы dQ_ск элементарных струек толщиной dy на   радиусе y  при скорости струй (рис. 14.6) u:

dQ_ск = 2py ^.dy^.u.

После интегрирования этого выражения в пределах от r до R и подстановки результата в (14.6) получаем:

 

Рис. 14.6. Эпюра скоростей спутного потока.

.

Аппроксимация этой зависимости степенной функцией дает результат:

K_ск=0,5a^0,38 ,                                          (14.15)

где a= r/R=d_н/D.

Формула (14.15) получена в предположении, что течение вязкой жидкости ламинарное. Однако она вполне применима и при турбулентном режиме течения.

14.2.3. Расчет коэффициента К_ск для случая, когда в скважине вязкопластичная (бингамовская) жидкость.

Картина движения вязкопластичной жидкости будет существенно отличаться от описанной для вязкой жидкости.

Предположим, что при скорости u_т1 (рис. 14.7) в кольцевом пространстве, заполненном ВПЖ, сформировалась эпюра t_R1 - t_r1. И если при этом динамическое напряжение жидкости равно t_o, то становится очевидным, что при y > r_o жидкость останется без движения (поскольку t будет меньше t_o), образовав “структурную” оболочку из неподвижного бурового раствора на стенке скважины.

На рис. 14.7 показаны три эпюры напряжений, соответствующие разным скоростям движения колонны (u_т1 <u_т2 < u_т3). При скорости u_т2 напряжения на стенке скважины равны t_o, что соответствует случаю, когда r = r_o.

Воспользуемся уравнением (14.10), подставив в него реологическую функцию

j(t)=(t –t_o)/h .        (14.16)

Интегрирование полученного выражения в пределах от t до t_o (до поверхности “структурной” стенки, где скорость равна нулю) дает результат:

.  (14.17)

На поверхности трубы u=u_т, а t  = t_r . Следовательно,

 

Рис. 14.7. Образование “структурной” оболочки на стенке скважины.

. (14.18)

Нетрудно показать, воспользовавшись формулой (14.7), что t_o/t_r=r/r_o, а t_o/t =y/r_o . Тогда уравнения (14.17) и (14.18) примут соответственно вид:

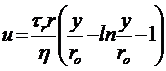,                                    (14.19)

 

.                                  (14.20)

Разделив (14.19) на (14.20), получаем:

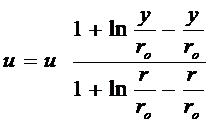.                           (14.21)

Это уравнение справедливо для интервала изменения y:

r_o ³ y ³ r.

В “структурной” оболочке (y ³ r_о) скорость u=0.

Расход спутного потока найдем тем же методом суммирования расходов элементарных кольцевых потоков dQ_ск , как и для вязких жидкостей:

.

Интегрирование после подстановки u по (14.21) дает результат:

Q_ск = y[(r_o³- r³)/3 - r² ln(r_o /r)/ 2 - (r_o² - r²)/4] ,                 (14.22)

где

.

Чтобы найти искомую величину K_ск, обратимся к формуле (14.6). В результате получим:

 .              (14.23)

Для того чтобы воспользоваться этой формулой, нужно прежде определить величину r_o. Такую возможность предоставляет уравнение (14.18). Если задаться u_т, то величину t_r можно найти численным методом, а затем вычислить r_o по формуле:

r_o=t_rr/t_o.                                                       (14.24)

В общем случае расчетный внутренний радиус “структурной” оболочки r_o может оказаться как меньше, так и больше R. Описанная выше методика, формулы (14.18), (14.21), (14.22) и (14.23), справедливы только для этого случая, когда r_o<R.

На рис. 14.8 приведен сравнительный пример распределения скоростей увлекаемого трубами потока в заколонном пространстве при использовании различных жидкостей при одной и той же скорости движения колонны труб. Видно, что количество жидкости, вовлекаемой трубами в движение существенно меньше, когда в скважине вязкопластичная жидкость.

С увеличением скорости движения колонны или с уменьшением t_o толщина неподвижной жидкостной оболочки уменьшается. Оболочка исчезает при r_o>R. Этот случай требует специального рассмотрения.

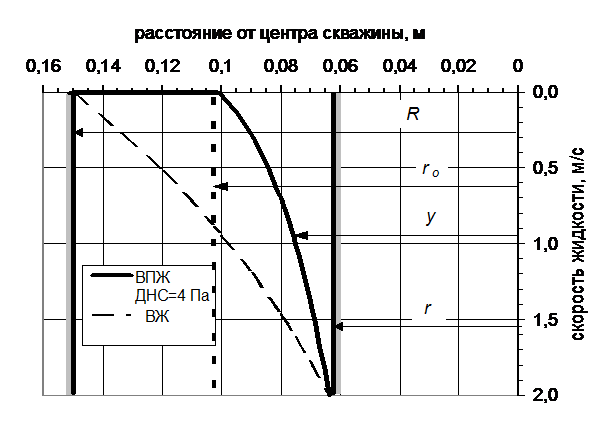
Рис. 14.8. Эпюры скоростей увлекаемого трубой потока вязкопластичной и вязкой жидкостей в заколонном пространстве при спуске бурильной колонны в скважину диаметром 300 мм со скоростью 2 м/с.

 

Если уравнение (14.10) с учетом реологической функции (14.16) проинтегрировать в пределах от t_r  до t_R , то получим:

- уравнение для определения скорости спутного потока:

 ;                      (14.25)

- уравнение для определения напряжения на стенке трубы при заданной скорости движения (после замены отношений напряжений на отношение радиусов):

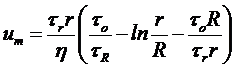;                        (14.26)

- уравнение для определения скорости потока на любом расстоянии y от оси скважины при заданной скорости движения колонны u_т:

 ;                          (14.27)

- искомую формулу для определения К_ск :

, (14.28)

где

A₁=t_oR/(t_rr); A₂=t_o/(t_rr); .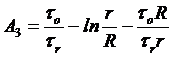

Рис. 14.9. Изменение коэффициента К_ск в зависимости от динамического напряжения сдвига бурового раствора: диаметр долота – 216 мм, диаметр труб - 127 мм, структурная вязкость буровых растворов - 0,02 Па_*с.

 

Величина t_r , как ранее отмечалось, определяется численным методом из уравнения (14.26).

 На рис. 14.9 приведен пример зависимости К_ск от t_o  для некоторого конкретного соотношения диаметров скважины и трубы.

Расчеты показали, что:

- при t_o ® 0 К_ск приближается к значению, равному К_ск для вязких жидкостей, рассчитанному по формуле (14.25);

- при малых t_o (ориентировочно до 3 Па), когда на стенке скважины не формируется “структурная” оболочка, расчет ведется для случая, когда R<r_o ;

- при t_o >3 Па имеет место существенное уменьшения спутного (увлекаемого трубами) потока и величины К_ск ;

- применение буровых растворов, обладающих структурной прочностью, сопровождается значительным, подчас кратным, уменьшением Q_ск , что обеспечивает уменьшение величины Q_экв .

14.2.4. Расчет коэффициента К_ск для случая, когда в скважине псевдопластичная (степенная) жидкость.

В последние годы, в связи с широким применением полимер-глинистых растворов с малым содержанием твердой фазы, все большее применение находят псевдопластичные жидкости, тяготеющие к степенным реологическим моделям с реологической функцией

j(t)=(t /K)^1/n .                                                (14.29)

Если подставить эту функцию, как в предыдущих случаях с вязкопластичными жидкостями, в уравнение (14.10) и затем проинтегрировать последнее в пределах от t до t_R , то, с учетом соотношения t_R=t_rr/R, получим:

,                   (14.30)

где

a = 1/n - 2.

На стенке трубы u = u_т , а t = t_r . После несложных преобразований имеем:

.                    (14.31)

В отличие от предыдущих случаев в данном уравнении t_r можно выразить в явном виде:

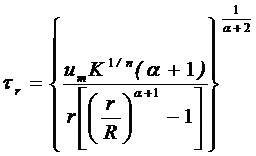.                        (14.32)

Заменяя в (14.30) отношения напряжений на отношения радиусов, приходим к результату:

.         (14.33)

 Чтобы найти Q_ск , нужно просуммировать расходы dQ_ск элементарных струек толщиной dy на радиусе y  при скорости струй u:

dQ_ск = 2py ^.dy^.u.                                           (14.34)

Подставив (14.33) в это уравнение и интегрируя в пределах от r до R, после некоторых преобразований получаем:

,                    (14.35)

где 

, , B₃=r^a+1, b=a+1.

Искомую величину коэффициента K_ск вычислим по формуле:

.                                 (14.36)

Анализ показал, что эпюра скоростей, а, следовательно, и величина К_ск, не зависят от индекса консистентности К, и зависят только от показателя реологического поведения жидкости n. Установлено также, что K_ск не зависит от скорости движения колонны.

На рис. 14.10 показаны зависимости u(y) при различных значениях n. Видно, что эпюра скоростей видоизменяется не столь сильно, как при вязкопластичных жидкостях с явно выраженной прочностью структуры. 

Рис. 14.11 иллюстрирует зависимость К_ск(n) для тех же расчетных условий, причем n=0,99 имитирует вязкую жидкость. Из анализа приведенной зависимости можно заключить, что влияние n на К_ск весьма существенно, и им пренебрегать не допустимо.

Итак, мы рассмотрели три случая, отличающиеся реологическими моделями жидкостей, которыми заполнена скважина. Установили, что при вязкой жидкости эпюра скоростей в заколонном пространстве(и, как следствие, величина К_ск,) зависят только от соотношения диаметров скважины и труб. 

Наиболее сложным является вариант применения вязкопластичной (бингамовской) жидкости, состоящий из двух подвариантов в зависимости от соотношения r_o и R, когда вначале нужно определить r_o, чтобы идентифицировать конкретный подвариант решения, затем вычислить t_r на стенке трубы и, наконец, определить искомую величину К_ск . Установили также, что при использовании степенной жидкости К_ск зависит от реологических параметров, но только от показателя реологического поведения n.

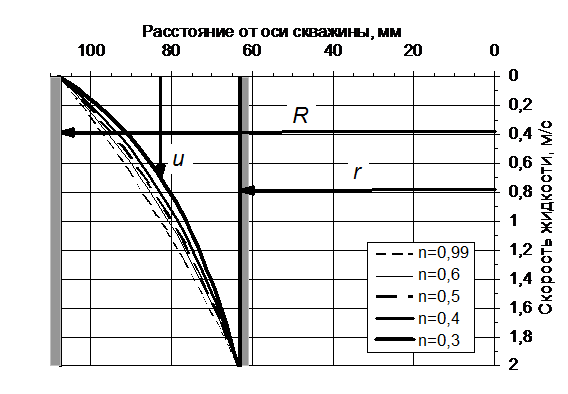
Рис. 14.10. Распределение скоростей жидкости в заколонном пространстве при степенной жидкости: диаметр скважины 215,9 мм,

диаметр труб - 127 мм.

 

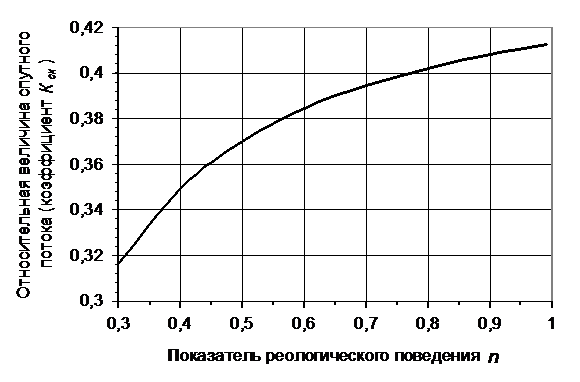
Рис. 14.11. Зависимость коэффициента К_ск от показателя реологического поведения n: условия расчета те же, что на рис. 14.10.

14.3. Методика расчета допустимой скорости спуска (подъема) "закрытой" колонны в скважине.

Данная задача является обратной по отношению к описанным выше и предполагает введение технологических ограничений на величину либо гидродинамического давления, либо общего давления на “слабый” пласт р_сл (с добавлением гидростатического).

Решение этой задачи сводится к определению такой скорости спуска u_т.доп колонны, при которой выполняется равенство

р_сл=ρgL_сл+р_гд.

Задача является типично компьютерной, поскольку требуется организация итерационного цикла по опредедлению искомого р_гд  путем изменения u_т .

Задача определения р_гд, р_гд.доп, u_т и u_т.доп существенно осложняется тем, что не известен расход жидкости, устремляющийся, например, при спуске колонны, в трубы. Решение задачи приведено в разделе 15.

 

Часть III. Проектирование и оптимизация гидравлических
 программ буровых процессов

15. Расчет гидродинамических давлений при равномерном
движении “открытых” трубных колонн в скважине.

В разделе 14 изложена (с обоснованием) методика расчета гидродинамического давления, возникающего при движении “закрытой” колонны, когда жидкость не может ни поступать внутрь труб при их спуске, ни вытекать из труб при подъеме. Нет нужды доказывать, что “открытые” колонны труб (если долотные отверстия не забиты или в колонне нет обратного клапана, а также, например, нет пластоиспытателя) создают меньшие по величине гидродинамические давления. Трубное пространство, куда при спуске устремляется (под действием возникающего давления) часть вытесняемой жидкости, является как бы каналом “утечки” давления.

 15.1. Методика расчета гидродинамического давления
при равномерном движении “открытой” колонны труб.

Представим себе двухразмерную бурильную колонну (рис. 15.1), составленную из УБТ диаметром d₁ и бурильных труб диаметром d₂ в скважине диаметром D. Пусть колонна заканчивается долотом с заданной площадью сечения промывочных каналов (на рис. 15.1 промывочный узел представлен условно одним отверстием).

При равномерном движении вниз в колонну устремляется жидкость с некоторым установившимся расходом Q_в, являющимся частью расхода вытеснения Q_вт:

или

.

Иначе говоря, если часть потока “уходит” с расходом Q_в в трубы, то ровно на столько убывает расход вытеснения как за УБТ, так и за бурильными трубами. А поскольку эквивалентный расход Q_экв состоит из Q_вт и Q_ск (см. часть II, раздел 14), то и Q_экв уменьшается на каждом участке на Q_в. Итак, для “открытой” колонны эквивалентный расход равен Q_экв за трубой диаметром d_i равен Q_экв для “закрытой” колонны за вычетом Q_в:

Q_экв.i= Q_cк.i + Q_вт.i - Q_в

или более конкретно (с заменой d_i на d_нi):

.             (15.1)

Если бы было известно заранее Q_в, то не было бы никаких проблем с определением Q_экв и, следовательно, р_гд. Значит, нужно еще одно уравнение или условие, обеспечивающее определение Q_в.

Расход Q_в поддерживается давлением р_в, а оно неизбежно равно р_гд в заколонном пространстве:

р_в=р_гд.                    (15.2)

Следовательно, расход Q_в должен быть точно таким, чтобы выполнялось условие (15.2).

Величина р_в численно равна потерям давления при движении жидкости по трубам снизу вверх (как при “обратной” промывке).

Чтобы найти Q_в для конкретного случая спуска, нужно, предварительно задавшись u_т1, выбрать первое ориентировочное значение Q_в1. Вычислить потери в трубах р_в (по изложенным в разделах 4…11 методикам) и прибавить к ним перепад на долоте:

,         (15.3)

где μ_сп=0,85 (резкое сужение при входе жидкости в насадки снизу).

Приняв Q_в=Q_в1, по формуле (15.1) вычислим Q_эквi и, пользуясь изложенной ранее методикой (см. раздел 14, часть II), находим р_гд1. Если теперь выяснится, что р_гд1>р_в1, то нужно повторить расчет р_в и р_гд при увеличенном на некоторую величину расходе Q_в2. Если же неравенство будет противоположное, то Q_в нужно уменьшать. И продолжать пересчитывать до тех пор, пока не выполнится условие (15.2). В связи с тем, что в процессе изменения Q_в от малых до больших значений вполне возможен переход от структурного (ламинарного) режима к турбулентному, расчет р_гд сведется к вычислительной процедуре с использованием разных формул в зависимости от соотношения Q_в и Q_кр на различных участках (секциях) трубного пространства. Такие расчеты правильнее всего поручать ЭВМ. Более того, задача определения р_гд при движении “открытой” колонны, предполагает организацию итерационного цикла для предварительного определения Q_в, что является типично “компьютерной” задачей.

 15.2. Расчет допустимой скорости движения “открытой”
колонны нефтепромысловых труб.

Предыдущую задачу назовем прямой задачей: задаемся u_т и определяем, какое при этой скорости будет р_гд. А теперь рассмотрим обратную задачу: нужно найти скорость u_т, при которой давление на “слабый” пласт р_сл=ρgL_сл+р_гд достигает предельно допустимого значения (L_сл – глубина расположения кровли “слабого” пласта).

Вырисовывается следующий алгоритм решения этой еще более, чем предыдущая, "компьютерной" задачи.

Вначале задаемся u_т (произвольно); затем задаемся р_в (тоже произвольно); проверяем условие р_в=р_гд; затем, меняя постепенно (ступенчато) Q_в, добиваемся выполнения этого условия и принимаем р_в (или р_гд, что одно и тоже) за искомое значение р_гд. До этого момента реализуется алгоритм решения уже известной нам прямой задачи.

Далее начинается новое. Скорее всего, абсолютное давление на слабый пласт р_сл окажется либо больше, либо меньше допустимого давления, например, давления гидроразрыва р_гр. Если р_сл<р_гр, то нужно наметить новую скорость u_т, превышающую предельную. В противном случае - поступить наоборот. Решению соответствует скорость u_т, при которой р_сл=р_гр. Но (и это главное), меняя u_т, придется провести заново поиск Q_в, чтобы рассчитать р_гд. И если и в этом случае р_сл¹р_гд, то придется снова изменить u_т и т.д. Таким образом, программа для ЭВМ должна иметь два расчетных цикла. Один – для поиска Q_в и р_гд. Второй, включающий в себя первый, – для определения u_т.доп, при которой выполняется условие р_сл=р_гд.

Таким образом, в случае “открытой” колонны при каждой новой скорости спуска (подъема) u_т в итерационном цикле осуществляется внутренний итерационный цикл с целью определения Q_в и р_гд . В реальном масштабе времени решение такой задачи под силу только ЭВМ.

Знание величины Q_в позволяет прогнозировать перелив жидкости (“сифон”) из труб при спуске колонны, например, после наворота пустой свечи. Для этого достаточно сравнить скорость спуска труб со средней скоростью движения жидкости в трубах верхней секции v_в. Если v_в > u_т , то перелив неизбежен, и даже можно предсказать, в какой момент спуска свечи начнется перелив жидкости.

Эта методика определения р_гд и u_т.доп для "открытых" колонн впервые разработана и реализована на ЭВМ в 1977 году П.Ф. Осиповым [4,5]. Значительно позднее аналогичная методика опубликована в работе [2].

 

---

Дата добавления: 2018-06-27; просмотров: 699; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!