Первая подструктура - Топологическая.
Она помогает оперировать такими характеристиками, непрерывно - разрывно, связно- несвязно ,принадлежит не принадлежит, внутри – вые, порознь – вместе.
Решающий ,у которого преобладает эта подструктура мышления, не любит торопиться. Каждое действие он делает очень подробно ,не пропуская ни одного звена. Это тонкий аналитик, он все проверит , не пропустит ошибок, отсюда и медлительность.
Вторая подструктура - Проективная.
Тот, у кого преобладает проективная подструктура предпочитает изучить любой математический объект с различных точек зрения, искать и находить различные применения предмета в практике .
Решающий любит планировать, он не сделает первого шага, если не видит следующего.
Он поражает нас широтой своего математического мышления, способностью отыскивать и предлагать совершенно неожиданные подходы и аспекты решения.
Третья подструктура - Порядковая.
Тот, у кого преобладает эта подструктура предпочитают сравнивать и оценивать в общем качественном виде: равно – не равно , больше – меньше, ближе – дальше , выше – ниже , и т. д. Ему важна форма объекта ,их соотношение , форма движения.
Четвертая подгруппа - Метрическая.
Акцентируется внимание на количественные характеристики. Они заворожены числом.
Главный вопрос: Сколько? Он всегда выясняет, какова длина отрезка и т.д. Ему трудно понять, что ответ может не иметь числового значения. Он не любит решать задачи в общем виде. Решать задачи в общем виде не в его правилах. Он предпочитает решение по действиям, результатом каждого, из
|
|
|
которых, является число.
Пятая подгруппа – Алгебраическая.
Стремится по возможности комбинациям. Он – торопыга. Не хочет подробно записывать, объяснять все шаги решения или обосновать собственные действия. Он «великий комбинатор», думает и делает быстро, фонтанирует идеи, предположения и гипотезы решения, но при этом часто ошибается.
Доминантная подструктура математического мышления проявляет себя во всех математических действиях; и в зависимости от нее каждый выбирает свой индивидуальный метод решения.
Как утверждал знаменитый И. В. Гете:
« Каждый слышит только то, что он понимает.»
Каждую задачу человек должен решить своим индивидуальным способом и лишь после этого пытаться понять иные методы рассуждений.
Поясним все сказанное на примере решения одной задачи.
Задача:
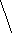
Трапеция разбита диагоналями на четыре треугольника. Докажите, что треугольники принадлежащие к боковым сторонам, равновелики.
|
|
|
Решение задачи « топологами».
Обычно топологи опираясь на принадлежность одних треугольников другим, выстраивают следующие доказательства:
Рассмотрим треугольник АВД и АСД. У них общее основание и равные высоты, проведенные к этому основанию.
Отсюда SАВД=SАСД.
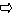SАВО=SАВД - SАДО=SАСД - SАДО=SСДО SАВО=SСДО.
Решение «проектистов».
SАВО=1/2 АО*h ; SВСО=1/2 CО*h, отсюда следует, что SАВО: SBCO= (1/2АО*h) : (1/2СО*h)=АО : СО.
Аналогично: SСДО : SВСО=ОД : ОВ из подобия треугольников ВСО и АДО следует, что АО : ОС=ДО : ОВ; значит SАВО : SВСО= SCDO : SBCO. Откуда
SАВD=SCDO.
Дата добавления: 2018-06-01; просмотров: 481; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!