Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности, общая точка называется точкой касания прямой и окружности.
расстояние от центра окружности до прямой меньше радиуса окружности:
Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки
расстояние от центра окружности до прямой равно радиусу окружности:
Мы доказали, что в данном случае общая точка единственная
расстояние от центра окружности до прямой больше радиуса окружности:
Мы доказали, что в данном случае окружность и прямая не имеют общих точек
8. Средняя Линия Трапеции
Средняя линия - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN средняя линия, AB и CD - основания, AD и BC - боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
9.Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h):
S=1\2ah
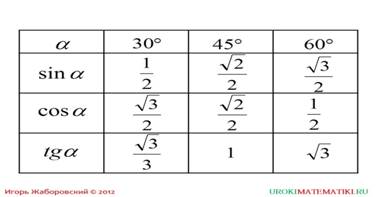
10 sin30°=cos60°=1/2
sin60°=cos30°=√3/2
sin45°=cos45°=√2/2
tg30°=ctg60°=1/√3
tg60°=ctg30°=√3
tg45°=ctg45°=1
|
|
|
11. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
Поскольку в треугольнике три стороны, треугольник имеет три средние линии.
12.Угол с вершиной в центре окружности называется центральным углом
Градусная мера центрального угла равна градусной мере соответствующей дуги окружности:
∡AOB=∪AB.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Вписанный угол измеряется половиной дуги, на которую он опирается:
∡ACB=1\2∪AB.
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, равен 90°.
У каждой дуги есть градусная мера. Сумма градусных мер двух дуг с общими концами равна 360°. Если отрезок, соединяющий концы дуги, является диаметром окружности, то дугу называют полуокружностью. Градусная мера полуокружности равна 180°
13. Свойства параллелограмма
1. Противоположные стороны параллелограмма равны:
AB=DC, BC=AD
2. Противоположные углы параллелограмма равны:
|
|
|
∢A=∢C, ∢B=∢D
3. Диагонали параллелограмма точкой пересечения делятся пополам:
BO=OD, AO=OC
4. Диагональ делит параллелограмм на два равных треугольника:
треугольники ABC и CDA равны.
5. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180 градусам: ∢A+∢D=180°
6. Накрест лежащие углы при диагонали равны:
∢BAC=∢ACD, ∢BCA=∢CAD
14. Центром описанной около прямоугольноготреугольника окружности является середина гипотенузы. Центр описанной около тупоугольноготреугольника окружности лежит вне треугольника. где a , b , c – стороны треугольника, A , B , С – углытреугольника, R – радиус описанной окружности.
15.Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
Свойство 1. Площадь фигуры является неотрицательным числом.
Свойство 2. Площади равных фигур равны.
Свойство 3. Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.
Еще нужна фигура, которую мы примем за эталон для измерения площади, ¾ единицу площади. При этом не следует забывать, что уже имеется единица измерения длины.
Свойство 4. За единицу измерения площади принимается площадь квадрата со стороной, равной 1 единице длины.
Другими словами, площадь квадрата со стороной, равной 1 единице длины, равна 1 единице площади, или 1 квадратной единице. Например, площадь квадрата со стороной 1 метр равна одному квадратному метру
Фигуры, имеющие равные площади, называтся равновеликими.
|
|
|
16. Биссектрисы треугольника пересекаются в одной точке.
17.
1. Четырёхугольник является параллелограммом, если его противоположные стороны попарно равны.
2. Четырёхугольник является параллелограммом, если его диагонали пересекаются и точкой пересечения делятся пополам.
3. Четырёхугольник является параллелограммом, если две его стороны параллельны и равны.
18.
1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.
2.Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.
3. Если расстояние от центра окружности до прямой равна радиусу, то у прямой и окружности одна общая точка.
19. Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин B и C к стороне AD .
Прямоугольные треугольники ABE и DCF равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
|
|
|
Параллелограмм ABCD и прямоугольник EBCF — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD SEBCF=SEBCD+SDCF
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC SABCD=BE⋅BC=BE⋅AD
Если обозначить сторону через a, высоту через h, то:
Sп−гр=a⋅h
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
20.
Теорема 5. Биссектрисы треугольника пересекаются в одной точке.
Теорема 6. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Теорема 7. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Теорема 8. Высоты треугольника или их продолжения пересекаются в одной точке.
21.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
22. Отношение периметров двух подобных треугольников равно коэффициенту подобия треугольников PABC\PDEF=k.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия SABC\SDEF=k2.
Дата добавления: 2018-06-01; просмотров: 1395; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
