Математические модели элементарных измерительных сигналов
Дельт а-фу н к ц и я. Рассмотрим теоретическую модель бесконечно короткого импульса с бесконечно большой амплитудой (рис. 4.5, а), аналитически определяемого формулой
Площадь такого импульса всегда равна единице:
Функцию δ(t) называют дельта-функцией, единичным импульсам, функцией Дирака, и она имеет физическую размерность циклической частоты — с^-1. При сдвиге дельта-функции по оси времени на интервал t0 (рис. 4.5, а) определения (4.11) и (4.12) необходимо записать в более обшей форме:
Дельта-функция обладает важнейшим свойством, благодаря которому она получила широкое применение в математике, физике, радио- и измерительной технике. Пусть имеется некоторая непрерывная функция времени f(t).
Единичная функция. Предельное, упрощенное аналитическое вы-ражение данного сигнала (рис. 4.5, б) принято записывать так:
Функцию σ(t) называют единичной функцией, функцией включения или функцией Хевисайда.
Спектральная плотность гармонического сигнала. Определим спектральную плотность сигнала u(t)= cos(ω0t)- Подставив в прямое преобразование Фурье (4.9) заданный сигнал, и воспользовавшись формулой Эйлера e^x = cosx + jsinx, находим:
Последнее соотношение можно записать в следующем виде:
Итак, гармоническому (в данном случае косинусоидальному) сигналу с конечной амплитудой соответствует декретный спектр, состоящий из двух линий бесконечно большой амплитуды в виде дельта-функций, расположенных симметрично относительно нуля на частотах -ω0 и ω0 (рис. 4.6).
|
|
|
По аналогии с косинусоидальным сигналом нетрудно показать, что синусоидальному сигналу u(t)= sin(ω0t) отвечает спектральная плотность
Здесь знак минус — следствие нечетности функции синуса.
Экспоненциальный импульс. Это сигнал с «полу бесконечной» длительностью (рис.4.7,а) и при единичной амплитуде описывается как
где а > 0 — вещественный параметр.
Постоянный сигнал (напряжение, ток) — самый простой из элементарных сигналов
Методы измерений энергетических параметров сигналов
Измерительные приборы
Сигнал как материальный носитель информации представляет собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой физической величиной. Такой параметр называют информативным параметром.
Измерительный сигнал – это сигнал, содержащий количественную информацию об измеряемой физической величине. Измерительные сигналы чрезвычайно разнообразны.
По характеру измерения информативного и временного параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые.
Аналоговый сигнал – это сигнал, описываемый непрерывной или кусочно-непрерывной функцией 
|
|
|
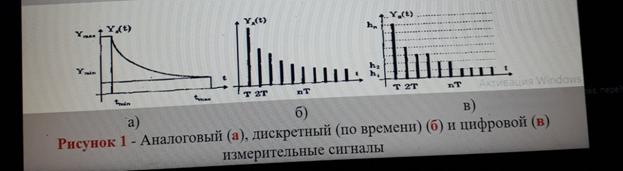
Дискретный сигнал – это сигнал, изменяющийся дискретно во времени или по уровню
Цифровые сигналы – квантование по уровню и дискретные по времени сигналы, которые описываются квантованными решетчатыми функциями (квантованными последовательностями), ряд дискретных значений – уровней квантования h1, h2, …, hn
Квантование – операция замены истинных мгновенных значений входной величины ближайшими фиксированными величинами из некоторой известной совокупности дискретных значений, называемых уровнями квантования.
Дата добавления: 2018-06-01; просмотров: 499; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!