Статистическая обработка результатов измерений.
Статистическая обработка результатов измерений – обработка измерительной информации с целью получения достоверных данных. Разнообразие задач, решаемых с помощью измерений, определяет и разнообразие видов статистической обработки их результатов.
Задача статистической обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится истинное значение.
Статистическая обработка используется для повышения точности измерений с многократными наблюдениями, а также определения статистических характеристик случайной погрешности.
Для прямых однократных измерений статистическая обработка менее сложна и громоздка, что значительно упрощает оценку погрешностей.
Статистическую обработку результатов косвенных измерений производят, как правило, методами, основанными на раздельной обработке аргументов и их погрешностей, и методом линеаризации.
Наиболее распространенные совместные измерения обрабатываются разными статистическими методами. Среди них широко известен и часто применяется метод наименьших квадратов.
Прямые измерения с многократными наблюдениями.
Необходимость в многократных наблюдениях некоторой физической величины возникает при наличии в процессе измерений значительных случайных погрешностей. При этом задача обработки состоит в том, чтобы по результатам наблюдений определить наилучшую (оптимальную) оценку измеряемой величины и интервал, в котором она находится с заданной вероятностью. Данная задача может быть решена способом статистической обработки результатов наблюдений, основанным на гипотезе о распределении погрешностей результатов по нормальному закону.
|
|
|
Порядок такой обработки должен соответствовать государственному стандарту и рекомендациям по метрологии.
Итак, рассмотрим группу из n независимых результатов наблюдений случайной величины x, подчиняющейся нормальному распределению. Оценка рассеяния единичных результатов наблюдений в группе относительно их среднего значения вычисляется по формуле:
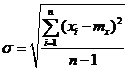
Поскольку число наблюдений в группе, на основании результатов которых выполнено вычисление среднего арифметического, ограничено, то, повторив заново серию наблюдений этой же величины, мы получили бы новое значение среднего арифметического. Повторив многократно наблюдения и вычисляя каждый раз их среднее арифметическое значение, принимаемое за результат наблюдений (измерений), обнаружим рассеяние среднего арифметического значения.
Характеристикой этого рассеяния является средний квадрат отклонения среднего арифметического:
|
|
|
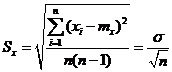
Среднее квадратичное отклонение среднего арифметического используется для оценки погрешности результата измерений с многократными наблюдениями.
Теория показывает, что если рассеяние результатов наблюдения в группе подчиняется нормальному закону, то и их среднее арифметическое тоже подчиняется нормальному закону распределения при достаточно большом числе наблюдений (n>50). Отсюда при одинаковой доверительной вероятности доверительный интервал среднего арифметического в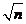 
ỳже, чем доверительный интервал результата наблюдений. Теоретически случайную погрешность результата измерений можно было бы свести к 0, однако практически это невозможно, да и не имеет смысла, так как при уменьшении значения случайной погрешности определяющим в суммарной погрешности становится значение не исключенных остатков систематической погрешности.
При нормальном законе распределения плотности вероятностей результатов наблюдений и небольшом числе измерений среднее арифметическое подчиняется закону распределения Стьюдента с тем же средним арифметическим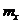 
. Особенностью этого распределения является то, что доверительный интервал с уменьшением числа наблюдений расширяемся по сравнению с нормальным законом распределения при этой же доверительной вероятности. В формуле для оценки доверительных границ случайной погрешности это отражается введением коэффициента tq вместо t:
|
|
|
Δx(P) = tσ= tqσ
Коэффициент распределения Стьюдента зависит от числа наблюдений и выбранной доверительной вероятности и находится по таблице. Например, для n=4 и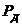 
=0,95 tq=3,182; n=5 при 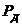=0,95 tq=2,776; для n=10 tq=2,262; n=15 tq=2,145 при той же 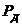=0,05.
Правила обработки результатов измерения с многократными наблюдениями учитывают следующие факторы:
- обрабатывается группа из n наблюдений (то есть группа ограничена);
- результаты наблюдений могут содержать систематическую погрешность;
- в группе наблюдений могут встречаться грубые погрешности;
- распределение случайных погрешностей может отличаться от нормального.
Обработка результатов наблюдения производится в следующей последовательности:
1) Исключить известные систематические погрешности из результатов наблюдения (введением поправки);
2) Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат наблюдений:
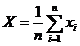
3) Вычислить оценку среднего квадратичного отклонения результата наблюдения:
|
|
|
4) Вычислить оценку среднего квадратичного отклонения среднего арифметического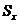 
по формуле:
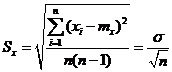
5) Проверить гипотезу о том, что результаты измерений принадлежат нормальному распределению.
6) Вычислить доверительные границы e случайной погрешности результата измерения при заданной вероятности P:
,
где 
- коэффициенты Стьюдента
7) Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерения.
При равномерном распределении НСП границы НСП вычисляют по формуле:
,
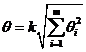где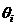 
- граница i-той НСП, k – коэффициент, определяемый принятой доверительной вероятностью (при 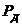=0,95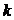 
=1,1); m – число неисключенных составляющих систематической погрешности.
8) Вычислить доверительные границы погрешности результата измерения.
границы погрешности результата измерения вычисляют по формуле:
,
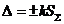где k – коэффициент, определяемый как
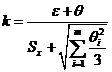
9) Записать результат измерения в регламентированной стандартом форме:
а) при симметричном доверительном интервале погрешности результата измерения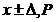 
, где x – результат измерения;
б) при отсутствии данных о виде функции распределения составляющих погрешности результата или при необходимости использования данных для дальнейшей обработки результатов, результат представляют в форме: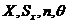 
Дата добавления: 2018-06-01; просмотров: 9977; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!