Оценка результата измерения и его среднего квадратического отклонения.
Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений.
Если результаты наблюдений можно считать принадлежащими к нормальному распределению, грубые погрешности исключают в соответствии с указаниями НТД.
За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей.
Примечание. Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.
Среднее квадратическое отклонение результата наблюдения оценивают согласно НТД.
Среднее квадратическое отклонение результата измерения оценивают по формуле
,
где xi - i-й результат наблюдения;
- результат измерения (среднее арифметическое исправленных результатов наблюдений);
n - число результатов наблюдений;
- оценка среднего квадратического отклонения результата измерения.
Доверительные границы случайной погрешности результата измерения. Погрешность и неопределённость результата измерения.
Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
|
|
|
При числе результатов наблюдений n> 50 для проверки принадлежности их к нормальному распределению по НТД предпочтительным является один из критериев: c2 Пирсона или w2 Мизеса-Смирнова.
При числе результатов наблюдений 50 >n> 15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий, приведенный в справочном приложении 1.
При числе результатов наблюдений n£ 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной настоящим стандартом, возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.
Доверительные границы e (без учета знака) случайной погрешности результата измерения находят по формуле
,
где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности P и числа результатов наблюдений n находят по таблице приложения 2.
Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности:
|
|
|
метода;
средств измерений;
вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.
При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.
Границы неисключенной систематической погрешности Q результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле
,
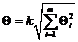где Qi - граница i-й неисключенной систематической погрешности;
k - коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности P = 0,95.
|
|
|
При доверительной вероятности P = 0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m> 4). Если же число суммируемых погрешностей равно четырем или менее четырех (m£ 4), то коэффициент k определяют по графику зависимости (см. чертеж).
График зависимости k = f (m, l)
k = f (m, l),
где m - число суммируемых погрешностей;
; кривая 1 - m = 2; кривая 2 - m = 3; кривая 3 - m = 4.
При трех или четырех слагаемых в качестве Q1 принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве Q2 следует принять ближайшую к Q1 составляющую.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
Дата добавления: 2018-06-01; просмотров: 1018; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!