Интегральные счётчики. Шифратор и дешифратор.

⇐ ПредыдущаяСтр 11 из 19Следующая ⇒

Шифратор (кодер) — (англ. encoder) логическое устройство, выполняющее преобразование позиционного кода в n-разрядный двоичный код. Шифратор выполняет функцию преобразования унарного кода в двоичный. При подаче сигнала на один из входов (обязательно на один, не более) на выходе появляется двоичный код номера активного входа.

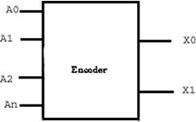
Таблица истинности для шифратора 4 в 2
A3 A2 A1 A0 X1 X0
0 0 0 1 0 0
0 0 1 0 0 1
0 1 0 0 1 0
1 0 0 0 1 1
Если количество входов настолько велико, что в шифраторе используются все возможные комбинации сигналов на выходе, то такой шифратор называется полным, если не все, то неполным. Число входов и выходов в полном шифраторе связано соотношением:

где n — число входов,m — число выходов.
Приоритетный шифратор отличается от шифратора наличием дополнительной логической схемы выделения активного уровня старшего входа для обеспечения условия работоспособности шифратора (только один уровень на входе активный). Уровни сигналов на остальных входах схемой игнорируются.
Дешифратор - это логическое устройство, работающее следующим образом: он получает на вход закодированный сигнал (двоичный, двоично-десятичный и т.п.), и выдает его на одном из n своих выходов. Существуют другие дешифраторы, преобразующие один код в другой.
Число входов дешифратора обычно меньше числа выходов.
Примеры дешифраторов:
• дешифратор 2 в 4; дешифратор 3 в 8; дешифратор 4 в 8;
• дешифратор двоично-десятичного кода в двоичный;
• дешифратор двоичного кода в код для 7-сегментного индикатора.
В соответствии с кодовой комбинацией на входах дешифратор выдает активный уровень (уровень логической единицы) на одном из выходов
. Двоичной комбинации 101 на входах соответствует логическая 1 на выходе Q5 (двоичное 101 равно десятичному 5), на остальных выходах будет 0.

Таблица истинности для дешифратора 3 в 8.
A2 A1 A0 Q7 Q6 Q5 Q4 Q3 Q2 Q1 Q0
0 0 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0 1 0 0
0 1 1 0 0 0 0 1 0 0 0
1 0 0 0 0 0 1 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0
1 1 0 0 1 0 0 0 0 0 0
1 1 1 1 0 0 0 0 0 0 0

Логические элементы и синтез логических элементов.

Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ? 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ? 0,4 В) – логическому нулю (ложь).

Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).

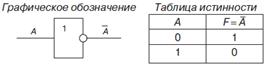
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).

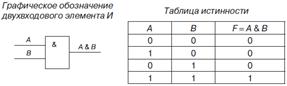
2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми

3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.

Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.

Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F₂, F₃, F₅и F₉(см. рис. 4.3).

Макстерном называют логическую функцию, которая принимает значение логического нуля только при одном значении логических переменных и значение логической единицы при других значениях логических переменных. Например, макстернами являются логические функции F₈, F₁₂, F₁₄и F_15.

Дата добавления: 2018-06-01; просмотров: 549; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!