Использование сложных сигналов и согласованного фильтра
Решение проблемы повышения помехозащищенности систем связи и управления достигается использованием различных методов и средств, в том числе и сигналов сложной формы (с большой базой).
Широкое практическое применение нашли сигналы на основе дискретных кодовых последовательностей, которые представляют собой последовательности символов длительностью Т, принимающих одно из двух значений: +1 или -1. Такие сигналы легко формируются и обрабатываются с использованием элементов цифровой и вычислительной техники.
Сложные сигналы должны удовлетворять ряду требований для достижения набольшей достоверности их приема:
а) корреляционная функция должна содержать значительный максимум (пик);
б) взаимная корреляционная функция любой пары сигналов из используемого ансамбля, определяющая степень их ортогональности, должна быть близка к нулю.
Достоинства и недостатки такие же, как и у ИКМ сигналов.
Влияние помехи в линии связи на передаваемый сигнал будет проявляться в изменении знака (полярности) элемента дискретного сигнала, т.е. в переходах вида 1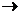 
-1, -1 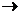1. При приеме с помощью согласованного фильтра это будет приводить к изменению формы сигнала на его выходе – уменьшению основного лепестка, увеличению боковых выбросов и, следовательно, к снижению помехоустойчивости приема.
Использование для передачи сложных сигналов обеспечивает эффективную защиту от импульсных, а иногда и от сосредоточенных помех.
|
|
|
Изобразим форму заданных сигналов при передаче по каналу связи символов «1» и «0» в предположении, что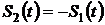 
, при этом длительность каждого из сигналов равна 
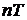, где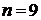 
– число элементов сложного сигнала:
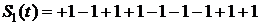
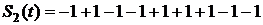
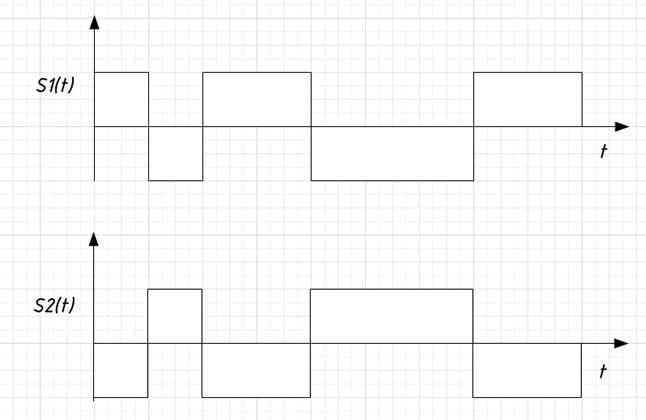
Рисунок 10 – Форма заданных сигналов при передаче по каналу связи
Импульсная характеристика согласованного фильтра
Импульсной характеристикой согласованного фильтра (СФ) называется реакция СФ при подаче на его вход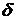 
-функции.
Для СФ импульсная характеристика – зеркальное отображение сигнала, с которым он согласован, сдвинутое на время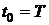 
.
, 
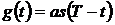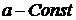
Импульсная характеристика фильтра, согласованного с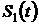 
:
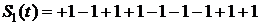
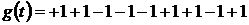
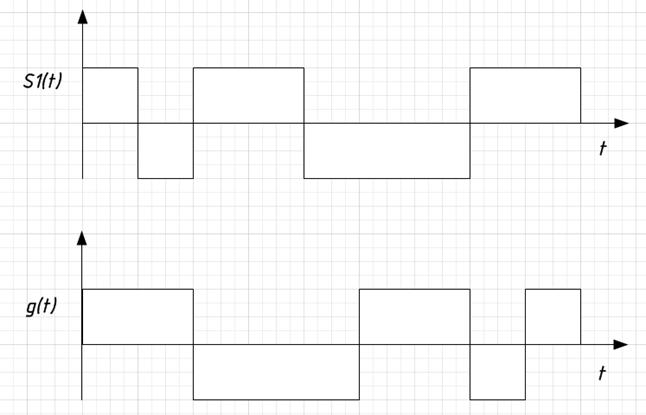
Рисунок 11 – Форма импульсной характеристики СФ
Схема согласованного фильтра для приема сложных сигналов. Форма сигнала на выходе согласованного фильтра при передаче символов «1» и «0»
Приведем схему СФ для заданного сигнала 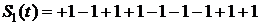и опишем, как формируется (поэлементно) сигнал на его выходе.
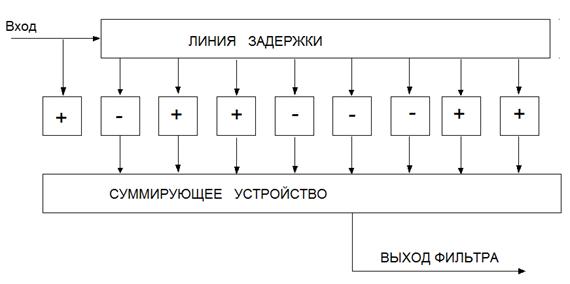
Рисунок 12.1 – Структурная схема согласованного фильтра
СФ для дискретных последовательностей может быть реализован в виде линии задержки с отводами (с общим временем задержки, равным длительности сигнала Тс), фазовращателей (инверторов) в отводах и суммирующей схемы, на выходе которой возникает импульс, равный сумме амплитуд всех элементов сигнала.
|
|
|
Устройства, реализующие согласованную фильтрацию дискретных сигналов, могут быть выполнены также и на основе регистра сдвига с количеством разрядов, равным количеству элементов в кодовой последовательности сигнала. В нем имеются перемножители и сумматоры. На вход перемножителей поступает принимаемая последовательность с разрядов регистра сдвига и опорная последовательность, совпадающая по виду с импульсной характеристикой входного сигнала, с эталонного регистра.
Сигналы с выходов всех разрядов перемножителей поступают на сумматор. Очевидно, что максимальный отклик на выходе сумматора будет наблюдаться тогда, когда кодовая последовательность полностью будет введена в регистр сдвига, т.е. в момент окончания входного сигнала.
Сигнал на выходе сумматора будет иметь вид ступенчатой функции. После сумматора может быть установлен интегратор, например, простейшая RC-цепочка, для «сглаживания» сигнала.
Т.к. СФ является коррелятором, то при подаче на его вход сигнала S(t), с которым он согласован, на выходе получим функцию корреляции входного сигнала:
|
|
|
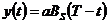
При воздействии на вход СФ флуктуационной помехи, функция взаимной корреляции равна нулю, т.к. сигнал и помеха являются независимыми функциями времени. Но так как для вычисления функции взаимной корреляции требуется бесконечно большое время интегрирования, а в нашем случае оно ведется за время T, то здесь она отлична от нуля.
При передаче сигнала «1» передается последовательность вида:
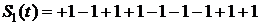
Пример расчета.
Пример расчета формы сигнала на выходе СФ:
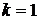
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | ||||||||
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | ||||||||
| 1 |
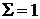
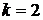
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | |||||||
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | |||||||
| 1 | -1 |
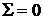
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | ||||||
| +1 | -1 | +1 | +1 | -1 | -1 | -1 | +1 | +1 | ||||||
| -1 | -1 | 1 |
|
|
|
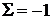
Далее аналогично.
Таблица 4
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| y(k) | 0 | 1 | 0 | -1 | 2 | -1 | -2 | -3 | 0 | 9 | 0 | -3 | -2 | -1 | 2 | -1 | 0 | 1 | 0 |
На выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, сдвинутую на длительность входного сигнала. При этом функция имеет значительный максимум (пик) (см. рисунок 12.2).
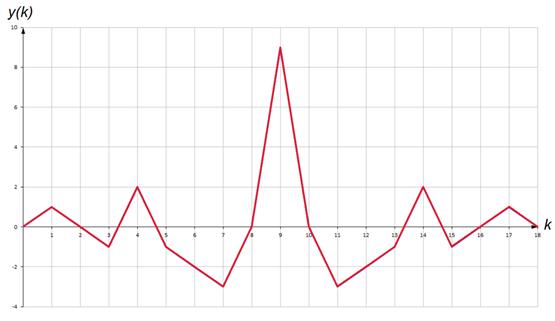
Рисунок 12.2 – Временная диаграмма сигнала на выходе согласованного фильтра
Рассчитаем форму помехи в предположении, что на вход фильтра поступает непрерывная последовательность знакопеременных символов:
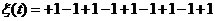
Принцип расчета аналогичен.
Расчетные данные сведены в таблицу 5.
Таблица 5
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| y(k) | 0 | 1 | -2 | 3 | -2 | 1 | -2 | 1 | 0 | 1 | 0 | -1 | 2 | -1 | 0 | -1 | 0 | 1 | 0 |
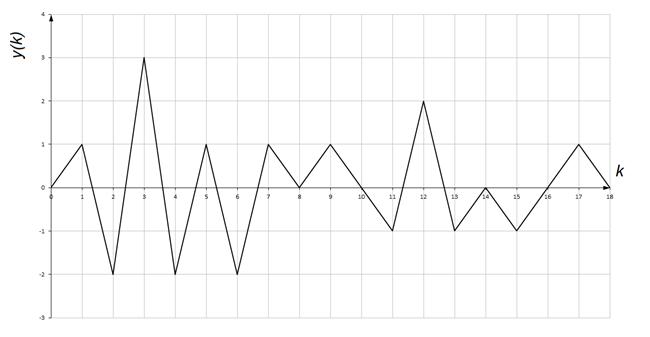
Рисунок 12.3 – Временная диаграмма сигнала на выходе согласованного фильтра, при вводе сигнала, с которым он не согласован
Дата добавления: 2018-05-30; просмотров: 878; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!