Структурная схема приемника ДФМ сигнала
В разрабатываемой системе связи задана фазовая манипуляция.
Выражение временной функции используемого сигнала:
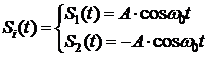
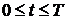
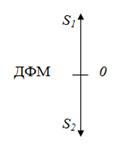
Рисунок 2.1 – Векторная диаграмма сигнала ДФМ
Из рисунка 2.1 видно, что расстояние между векторами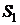 
и 
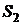равно длине вектора 
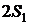. Энергия пропорциональна квадрату разности сигналов.
Система ФМ – является оптимальной, когерентной системой передачи двоичных сигналов. По сравнению с ЧМ – ФМ обеспечивает при одинаковой помехоустойчивости двойной выигрыш по полосе частот и по мощности, занимаемой передаваемым сигналом.
Так как при ФМ необходимо получать информацию о фазе принимаемого сигнала, то при этом приеме в обязательном порядке используют метод когерентного приема.
Структурная схема приемника ДФМ представлена на рисунке 2.2.
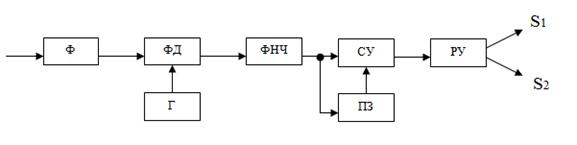
Рисунок 2.2 – Структурная схема приемника ДФМ сигнала.
Ф – полосовой фильтр; ФД – фазовый детектор; Г – гетеродин; ФНЧ - фильтр нижней частоты; РУ - решающее устройство; СУ – сравнивающее устройство;
ПЗ – полоса задержки.
Полосовой фильтр предназначен для предварительной фильтрации сигналов, для уменьшения влияния помех, с полосой пропускания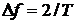 
, в присутствии только гауссовских помех не обязателен. Фазовый детектор используется в качестве корректора. Фильтр нижних частот - интегратора. Опорный гетеродин - генератор, частота и фаза колебаний которого полностью совпадают с частотой и фазой одного из сигналов.
|
|
|
Принятие решения приемником по одному отсчету
Сообщения передаются последовательностью двоичных символов «1» и «0», которые появляются с априорными вероятностями соответственно p(1)=0,27 и p(0)=0,73.
В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией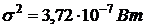 
. Приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), принимает решение по одному отсчету смеси сигнала и помехи 
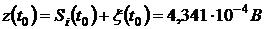на интервале элемента сигнала длительности T.
Отношением правдоподобия называется величина, определяемая выражением:
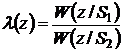, где
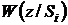- плотность вероятности того, что принятый сигнал 
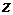образовался при передачи сигнала 
.
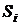Таким образом, отношение правдоподобия есть величина, равная отношению плотности вероятности того, что принятый сигнал 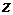образовался при передаче символа «1», к плотности вероятности того, что принятый сигнал образовался при передаче символа «0».
Свою очередь, выражение, стоящее справа называется пороговым отношением правдоподобия:
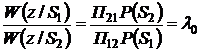, где
, 
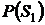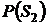- априорные вероятности,
, 
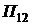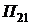- весовые коэффициенты.
Приемник, использующий отношение правдоподобия, работает следующим образом.
|
|
|
1. Анализируя поступающий на его вход сигнал, вычисляет отношение правдоподобия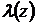 
.
2. По известным значениям 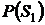и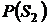 
, а также заданным 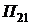и 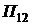, вычисляется пороговое отношение правдоподобия 
.
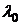3. Величина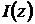 
сравнивается с 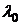, если 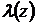> 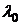, приемник выдает сигнал 
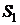, в противном случае сигнал .
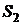Согласно критерию идеального наблюдателя, весовые коэффициенты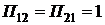 
. Тогда пороговое отношение правдоподобия принимает вид:
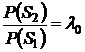
Критерий идеального наблюдателя широко применяется в системах связи, когда искажения любого сигнала одинаково нежелательны.
Плотности вероятностей найдём по формулам:
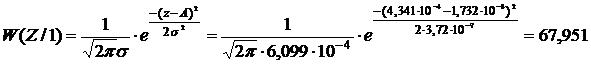
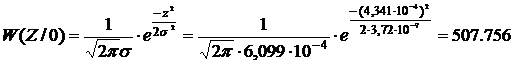
Для вычисления плотности распределения помехи применим формулу:
.
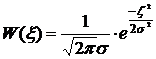Отношение правдоподобия:
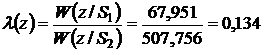
Пороговое отношение правдоподобия:
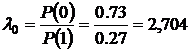
Т.к. >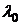 
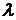, приемник выдает сигнал S2 и на выходе решающего устройства будет зарегистрирован «0».
Т.к. передача символа «0» соответствует паузе, то в этот момент в канале присутствует только помеха (мощность сигнала в паузе равна нулю), а, следовательно, плотности распределения огибающей помехи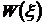 
и огибающей сигнала + помеха при передаче «0» 
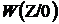будут совпадать. Что наглядно подтверждается графиками (см. рисунки 3.1 и 3.2).
Рассчитаем и построим функции распределения плотности вероятности для W(x), W(z/0) и W(z/1).
|
|
|
Таблица 1.
| Z, мВ | -5Z | -4Z | -3Z | -2Z | -Z | 0 | Z | 2Z | 3Z | 4Z | 5Z | 6Z | 7Z | 8Z |
| W(Z/1) | 0,0 | 0,0 | 0,0 | 0,1 | 1,2 | 11,6 | 68,0 | 239,9 | 510,3 | 654,1 | 505,1 | 235,1 | 65,9 | 11,1 |
| W(Z/0) | 1,2 | 11,4 | 66,9 | 237,5 | 507,7 | 654,1 | 507,7 | 237,5 | 66,9 | 11,4 | 1,2 | 0,1 | 0,0 | 0,0 |
Таблица 2
| x, В | -3s | -2s | -s | 0 | s | 2s | 3s | 4s |
| W(x) | 7,27 | 88,52 | 396,73 | 654,09 | 396,73 | 88,52 | 7,27 | 0,22 |
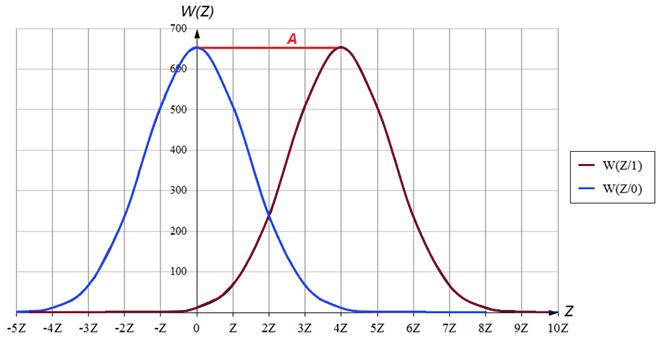
Рисунок 3.1 – Графики распределения плотности вероятностей W(Z/0), W(Z/1)
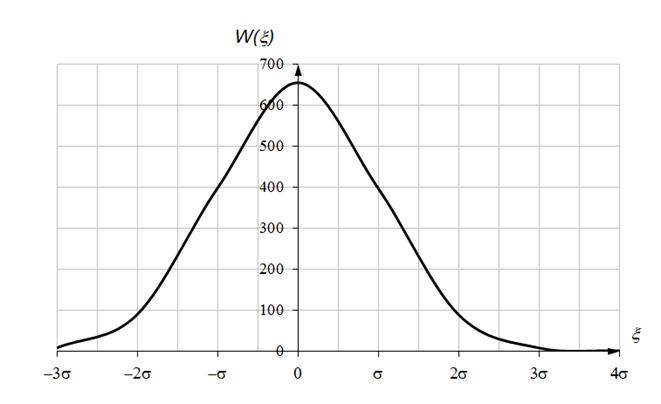
Рисунок 3.2 – График плотности распределения помехи
Дата добавления: 2018-05-30; просмотров: 1312; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!