Постановка краевой задачи для обыкновенного дифференциального уравнения
Пусть дано дифференциальное уравнение второго порядка
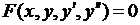
| (1.10) |
Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.
Найти функцию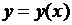 
, которая внутри отрезка 
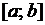удовлетворяет уравнению (110), а на концах отрезка — краевым условиям
  
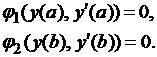
| (1.11) |
Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:
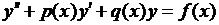
| (1.12) |
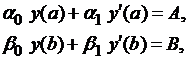
| (1.13) |
где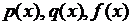 
– известные непрерывные на отрезке 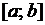функции, 
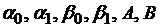– заданные постоянные, причем 
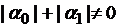и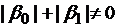 
.
Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей
Данный метод заключается в следующем.
Разбиваем отрезок 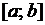на n равных частей с шагом 
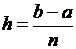и получаем точки 
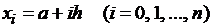, в которых требуется найти искомые значения 
.
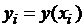Введем обозначения:
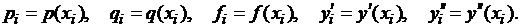
Заменим приближенно в каждом внутреннем узле производные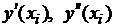 
конечно-разностными схемами:
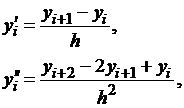
| (1.14) |
а на концах отрезка положим:
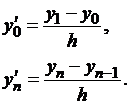
| (1.15) |
Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:
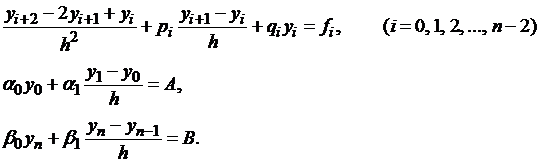
| (1.16) |
Получим линейную алгебраическую систему, содержащую n+1 уравнение с n+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.
Более точные формулы получаются, если заменить 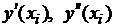центрально-разностными отношениями:
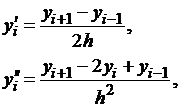
| (1.17) |
а на концах отрезка положить:
|
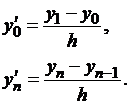
| (1.18) |
Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:
|
|
|
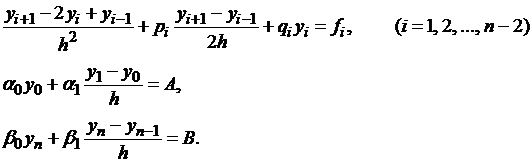
| (1.19) |
Пример 1.5.Методом конечных разностей найти решение краевой задачи:
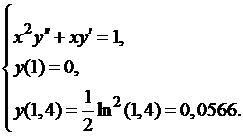
| (1.20) |
Решение:Используя формулы (1.17), заменяем уравнение (1.20) системой конечно-разностных уравнений
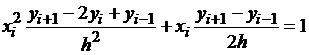
В результате приведения подобных членов получаем
 .
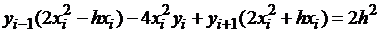| (1.21) |
Выберем шаг h, равный 0,1. Тогда получим три внутренних узла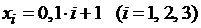 
. Написав уравнение (1.21) для каждого из этих узлов, получим систему:
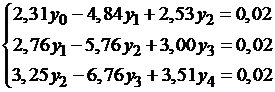
| (1.22) |
В граничных узлах имеем: 
.
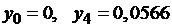Используя эти значения, решаем систему (1.22) и получаем:
.
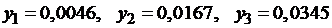Для сравнения приведем значения точного решения уравнения (1.18)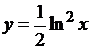 
в соответствующих точках: 
.
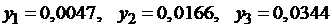Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.
Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.
Запишем уравнения системы (1.14) в виде:
,
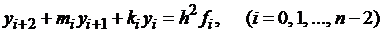где
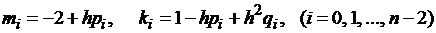
| (1.23) |
Полученную систему приводим к виду:
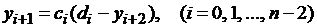
| (1.24) |
Числа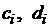 
последовательно вычисляются по формулам:
при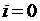 
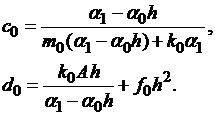
| (1.25) |
При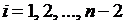 
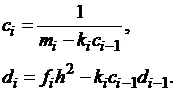
| (1.26) |
Вычисления производятся в следующем порядке.
|
|
|
Прямой ход.По формулам (1.23) вычисляем значения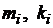 
. Находим 
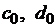по формулам (1.25). Затем вычисляем 
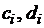по формулам (1.26) для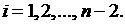 
Обратный ход. Из уравнения (1.24) при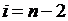 
и последнего уравнения системы (1.16) получаем:
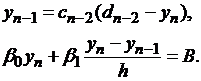
Решив эту систему относительно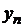 
, будем иметь
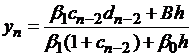
| (1.27) |
Используя уже известные числа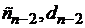 
, находим 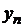. Затем вычисляем значения 
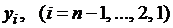, последовательно применяя рекуррентные формулы (1.22):
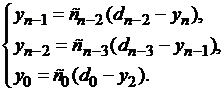
| (1.28) |
Значение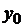 
находим из предпоследнего уравнения системы (1.16):
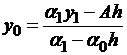
| (1.29) |
Таким образом, все вычисления «прогоняются» два раза.
Вычисления прямого хода заготавливают вспомогательные числа 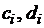в порядке возрастания индекса 
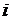. При этом для вычисления значений 
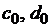используется краевое условие на левом конце отрезка интегрирования. Затем на первом шаге обратного хода происходит согласование полученных чисел 
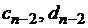с краевым условием на правом конце отрезка интегрирования, после чего последовательно получаются значения искомой функции 
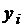в порядке убывания индекса .
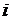Дата добавления: 2018-06-27; просмотров: 503; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!