Метод последовательных приближений
Nbsp;
Содержание
Примерный тематический план проведения лабораторных работ……...5
Глава 1. Приближенные методы решения обыкновенных дифферен-циальных уравнений……………………………………………………………5
1.1. Справочные материалы по приближенным методам решения обыкно- венных дифференциальных равнений…………………………………………..5
1.1.1. Постановка задачи Коши…………………………………………...5
1.1.2. Метод последовательных приближений…………………………..7
1.1.3. Метод Эйлера………………………………………………………11
1.1.4. Метод Эйлера–Коши……………………………………………....12
1.1.5. Метод Рунге–Кутта четвертого порядка…………………………13
1.1.6. Многошаговые методы. Метод Адамса. Методы прогноза–коррекции………........................................................................................16
1.1.7. Постановка краевой задачи для обыкновенного дифферен-
циального уравнения…………………………………………………….18
1.1.8. Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей……………………………….18
1.1.9. Приближенное решение обыкновенных дифференциальных уравнений методом прогонки……………………………………………21
1.2. Лабораторная работа № 1. Приближенное решение обыкновенных диф-ференциальных уравнений методом последовательных приближений..........22
1.3. Лабораторная работа № 2. Приближенное решение обыкновенных диф-ференциальных уравнений. Методы Эйлера, Эйлера–Коши, Рунге–Кутта………………………………………………….........................................25
|
|
|
1.4. Лабораторная работа № 3. Приближенное решение обыкновенных дифференциальных уравнений. Метод Адамса. Методы прогноза-коррекции………………………………………………………..………………26
1.5. Лабораторная работа № 4. Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей………………28
1.6. Лабораторная работа № 5. Приближенное решение обыкновенных дифференциальных уравнений методом прогонки…………………………..29
Глава 2. Приближенные методы решения дифференциальных уравне-
ний с частными производными……………………………………………..30
2.1 Справочный материал по приближенным методам решения диффе-ренциальных уравнений счастными производными…………………………30
2.1.1.Постановка задачи Дирихле. Приближенное решение уравнения Лапласа…………………………………………………………………...30
2.1.2. Итерационный метод решения системы конечно-раз-
ностных уравнений (процесс усреднения Либмана)…………………..32
2.2. Лабораторная работа № 6. Метод сеток для задачи Дирихле ………….35
2.3. Лабораторная работа № 7. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана)……………36
|
|
|
Глава 3. Приближенные методы решения интегральных уравне-
ний……………………………………………………………………………….36
3.1. Справочный материал по приближенным методам решения интег-ральных уравнений (уравнение Фредгольма второго рода)…………………36
3.2. Лабораторная работа № 8. Решение уравнения Фредгольмам
второго рода методом конечных сумм………………………………………..38
Глава 4. Статистическая обработка данных………………………………40
4.1. Справочный материал по статистической обработке данных………......40
4.2. Лабораторная работа № 9. Методы обработки статистических
данных …………………………………………………………………………..41
Список литературы……………………………………………………………...49
Примерный тематический план проведения лабораторных работ
В тематическом плане приведено примерное планирование часов, которые отводятся на каждую лабораторную работу.
В зависимости от используемого программного обеспечения число часов, необходимых для выполнения заданий, может быть уменьшено.
Тематический план проведения лабораторных работ
1. Приближенное решение обыкновенных дифференциальных уравнений методом последовательных приближений – 4 часа.
2. Приближенное решение обыкновенных дифференциальных уравнений. Методы Эйлера, Эйлера Коши, Рунге-Кутта – 4 часа.
|
|
|
3. Приближенное решение обыкновенных дифференциальных уравнений. Метод Адамса. Методы прогноза-коррекции – 4 часа.
4. Приближенное решение дифференциальных уравнений методом конечных разностей – 2 часа
5. Приближенное решение диф. уравнений методом прогонки – 4 часа.
6. Метод сеток для задачи Дирихле – 4 часа.
7. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана) – 4 часа.
8. Решение уравнения Фредгольма второго рода методом конечных сумм – 4 часа.
9. Метод обработки статистических данных – 4 часа.
Глава 1. Приближенные методы решения обыкновенных дифферен-циальных уравнений
Справочные материалы по приближенным методам решения обыкновенных дифференциальных равнений
Постановка задачи Коши
Рассмотрим обыкновенное дифференциальное уравнение первого порядка:
 . (1.1)
. (1.1)
Основная задача, связанная с этим уравнением – задача Коши состоит в следующем: найти решение уравнения (1.1) в виде функции  удовлетворяющей начальному условию:
удовлетворяющей начальному условию:
 . (1.2)
. (1.2)
|
|
|
Геометрически это означает, что требуется найти интегральную кривую  проходящую через заданную точку
проходящую через заданную точку  при выполнения равенства (1.1). Существование и единственность решения уравнения (1.1) обеспечивается следующей теоремой.
при выполнения равенства (1.1). Существование и единственность решения уравнения (1.1) обеспечивается следующей теоремой.
Теорема Пикара:Если функция f определена и непрерывна в некоторой области G, определённой неравенствами:
 (1.3)
(1.3)
и удовлетворяет в этой области условию Липшица по у:  , то на некотором отрезке
, то на некотором отрезке  , где h – положительное число, существует, и притом только одно, решение
, где h – положительное число, существует, и притом только одно, решение  уравнения (1.1), удовлетворяющее начальному условию
уравнения (1.1), удовлетворяющее начальному условию  .
.
Здесь М – постоянная (константа Липшица), зависящая в общем случае от а и b.
Если f(x, y) имеет ограниченную в G производную  , то при
, то при  можно принять
можно принять  .
.
В классическом анализе разработаны методы нахождения решений дифференциальных уравнений через элементарные (или специальные) функции. На практике эти методы очень часто оказываются либо совсем беспомощными, либо их использование требует трудных вычислений и времени.
Для решения практических задач созданы методы приближённого решения дифференциальных уравнений.
Пусть требуется на отрезке  [х0, х00+Н] найти решение уравнения (1.1) при начальном условии (1.2).
[х0, х00+Н] найти решение уравнения (1.1) при начальном условии (1.2).
Разобьём отрезок на п равных частей точками:  , где
, где  .
.
Численное решение дифференциального уравнения (1.1) заключается в том, что значение искомой функции 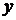 вычисляется в каждой точке
вычисляется в каждой точке 
 . При этом, как правило, для вычисления значения
. При этом, как правило, для вычисления значения  используется уже вычисленное значение
используется уже вычисленное значение  .
.
Для решения задачи Коши для обыкновенных дифференциальных уравнений существуют различные методы:
1. Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.
2. Графические методы, дающие приближенное решение в виде графиков.
3. Численные методы (табличные), при использовании которых искомая функция получается в виде таблицы.
Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений первого порядка вида (1.1).
Метод последовательных приближений
Рассмотрим задачу Коши для дифференциального уравнения первого порядка  с начальным условием
с начальным условием  .
.
Метод последовательных приближений состоит в том, что решение  , получают как предел последовательности функций
, получают как предел последовательности функций  , которые находятся по рекурсивной формуле
, которые находятся по рекурсивной формуле
 . (1.4)
. (1.4)
Если правая часть  в некотором замкнутом прямоугольнике
в некотором замкнутом прямоугольнике  , содержащем множество точек
, содержащем множество точек  , для которых выполняются условия
, для которых выполняются условия  удовлетворяет условию Липшица по
удовлетворяет условию Липшица по 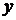 :
:
 ,
,
то независимо от выбора начальной функции последовательные приближения  сходятся на некотором отрезке
сходятся на некотором отрезке  к точному решению задачи Коши.
к точному решению задачи Коши.
Если  непрерывна в области
непрерывна в области  , то оценка погрешности приближенного решения
, то оценка погрешности приближенного решения  на отрезке
на отрезке  дается неравенством:
дается неравенством:
 , (1.5)
, (1.5)
где  , а число
, а число  определяется из условия:
определяется из условия:
 .
.
Пример 1.1. Найти три последовательных приближения решения уравнения:

с начальным условием  Оценить погрешность третьего приближения на отрезке
Оценить погрешность третьего приближения на отрезке 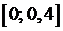 .
.
Решение. Учитывая начальное условие, заменим уравнение интегральным
 .
.
В качестве начального приближения возьмем  . Первое приближение находим по формуле (1.4):
. Первое приближение находим по формуле (1.4):
 .
.
Аналогично получаем второе и третье приближения:

 ,
,

Оценим погрешность последнего приближения по формуле (1.5). Так как функция  , то она определена и непрерывна во всей плоскости
, то она определена и непрерывна во всей плоскости  и в качестве
и в качестве 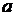 и
и  можно взять любые числа. Возьмем для определенности
можно взять любые числа. Возьмем для определенности 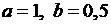 . При таких ограничениях получаем:
. При таких ограничениях получаем:
 ,
,
 .
.
Таким образом, на отрезке [0; 0.4] получаем
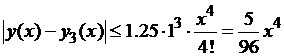 ,
,
и, следовательно:
 .
.
Замечание: Оценка погрешности по формуле (1.5) часто оказывается завышенной. Практически, применяя метод последовательных приближений, вычисления продолжают до такого 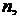 при котором значения
при котором значения  совпадают в пределах допустимой точности.
совпадают в пределах допустимой точности.
Пример 1.2. Дана система

с начальными условиями 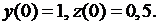 Методом последовательных приближений найти решение этой системы на отрезке [0; 0,3] с точностью до
Методом последовательных приближений найти решение этой системы на отрезке [0; 0,3] с точностью до  .
.
Решение: Записываем систему в интегральной форме:
 , ,
| 
|
используя начальные значения, из системы находим  ,
,  . В качестве начальных приближений выберем:
. В качестве начальных приближений выберем:
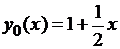 , ,
| 
|
При выборе начальных приближений используем первые два члена разложения функций 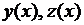 в окрестности точки
в окрестности точки 
Вычислим следующие приближения  и
и  :
:
 ,
,
 .
.
Аналогично получаем:
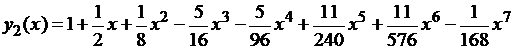 ,
,
 .
.
Оценим разности  и
и  на отрезке [0; 0.3]:
на отрезке [0; 0.3]:
,

Эти разности находятся в пределах заданной точности, причем члены, содержащие  , малы на отрезке [0; 0,3]. Следовательно, с заданной точностью можно положить
, малы на отрезке [0; 0,3]. Следовательно, с заданной точностью можно положить
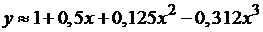 ,
,  .
.
Метод Эйлера
Рассмотрим дифференциальное уравнение  с начальным условием
с начальным условием  .
.
Выбрав достаточно малый шаг  , построим систему равноотстоящих узлов
, построим систему равноотстоящих узлов  , (
, (  ).
).
Приближенные значения 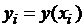 по методу Эйлера вычисляются последовательно по формулам:
по методу Эйлера вычисляются последовательно по формулам:
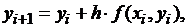 (
(  )
)
При оценке погрешности обычно используется двойной пересчет.
Если  – вычисленное значение
– вычисленное значение  с шагом
с шагом  , а
, а 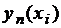 – соответствующее узловое значение, полученное с шагом h, то для ориентировочной оценки погрешности последнего значения можно использовать формулу:
– соответствующее узловое значение, полученное с шагом h, то для ориентировочной оценки погрешности последнего значения можно использовать формулу:

Пример 1.3. Применяя метод Эйлера, составить на отрезке [0,1] таблицу значений решения уравнения:
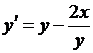
с начальным условием  , выбрав шаг
, выбрав шаг  .
.
Решение дифференциального уравнения приведено в таблице 1.1.
Таблица 1.1
Приближенное решение уравнения примера 1.3 методом Эйлера
| № шага | 
| 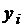
| 
| Точное решение

|
| 0 | 0 | 1,0000 | 0,2000 | 1,0000 |
| 1 | 0,2 | 1,2000 | 0,1733 | 1,1832 |
| 2 | 0,4 | 1,3733 | 0,1561 | 1,3416 |
| 3 | 0,6 | 1,5294 | 0,1492 | 1,4832 |
| 4 | 0,8 | 1,6786 | 0,1451 | 1,6124 |
| 5 | 1,0 | 1,8237 | 1,7320 |
Рассмотрим пример вычисления  :
:

 .
.
Для остальных значений 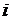 вычисления проводятся аналогично.
вычисления проводятся аналогично.
1.1.4. Метод Эйлера–Коши
Метод Эйлера–Коши является модификацией метода Эйлера. Вычисления табличных значений решения и оценка погрешности проводятся по следующим формулам.
 ,
,
 ,
,
 ,
,
где  – точное значение решения в узле
– точное значение решения в узле  ,
,  ,
, 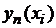 – приближенные значения решения в узле
– приближенные значения решения в узле  с шагом
с шагом  – соответственно.
– соответственно.
Таблица 1.2
Приближенное решение уравнения примера 1.3 методом Эйлера–Коши
| № шага | 
| 
| 
| Точное решение

|
| 0 | 0 | 1,0000 | 0,1867 | 1,0000 |
| 1 | 0,2 | 1,1867 | 0,1617 | 1,1832 |
| 2 | 0,4 | 1,3484 | 0,1454 | 1,3416 |
| 3 | 0,6 | 1,4938 | 0,1341 | 1,4832 |
| 4 | 0,8 | 1,6272 | 0,1263 | 1,6124 |
| 5 | 1,0 | 1,7542 | 1,7320 |
Рассмотрим применение метода Эйлера–Коши для примера 1.3, решенного выше методом Эйлера.
Покажем пример вычисления  :
:
 ,
, 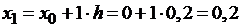 .
.

Остальные значения проводятся аналогично. Результаты счета приведены в таблице 1.2.
1.1.5. Метод Рунге–Кутта четвертого порядка
Рассмотрим метод Рунге–Кутта четвёртого порядка для нахождения численного решения уравнения (1.1) с начальным условием (1.2).
Пусть  является начальным условием (при
является начальным условием (при 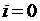 ), либо получено как результат предыдущего шага. Для получения следующего значения
), либо получено как результат предыдущего шага. Для получения следующего значения  вначале вычисляются числа:
вначале вычисляются числа:
 , (1.6)
, (1.6)
где h – шаг интегрирования.
Затем вычисляют:  .
.
Новое значение функции вычисляется по формуле:
 . (1.7)
. (1.7)
Метод Рунге–Кутта четвертого порядка является методом повышенной точности. На практике для контроля точности этого метода используется двойной счет пересчет.
Если  – вычисленное значение
– вычисленное значение  с шагом
с шагом  , а
, а  – соответствующее узловое значение, полученное с шагом h, то для приближенной оценки погрешности значения
– соответствующее узловое значение, полученное с шагом h, то для приближенной оценки погрешности значения  можно использовать формулу:
можно использовать формулу:
 .
.
Пример 1.4. Решить методом Рунге–Кутта уравнение на отрезке [0, 1] с шагом h = 0,2:
 .
.
Результаты вычислений оформим в виде таблицы 1.3.
Таблица 1.3
Результаты приближенного решения примера 1.4 методом Рунге–Кутта
четвертого порядка
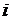
| 
| 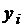
| 
| 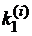
| 
| 
| 
|
| 0 | 0,0 | 1,0000 | 0,2000 | 0,1980 | 0,2000 | 0,1916 | 0,1972 |
| 1 | 0,2 | 1,1972 | 0,1916 | 0,1810 | 0,4000 | 0,1653 | 0,1799 |
| 2 | 0,4 | 1,3771 | 0,1653 | 0,1460 | 0,6000 | 0,1218 | 0,1448 |
| 3 | 0,6 | 1,5219 | 0,1217 | 0,0950 | 0,8000 | 0,0646 | 0,0941 |
| 4 | 0,8 | 1,6160 | 0,0646 | 0,0330 | 1,0000 | 0,0000 | 0,0326 |
| 5 | 1,0 | 1,6486 |
Покажем пример вычисления табличного значения  .
.

Для вычисления  надо вычислить
надо вычислить  :
:





Остальные значения  вычисляются аналогично.
вычисляются аналогично.
Дата добавления: 2018-06-27; просмотров: 580; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
