Энергетические уровни и спектральные линии излучения атомов в магнитном поле расщепляются.
Сегодня неизбежность существования эффектов подобного влияния кажется нам очевидной, поскольку мы знаем, что электроны и другие атомы обладают спином, то есть ведут себя подобно микроскопическим электрически заряженным волчкам, образующим вокруг себя магнитное поле, и, по сути, представляют собой микроскопические магниты. Чтобы понять его природу, проще всего обратиться к модели атома Бора и задуматься о том, как именно испускается свет. Электрон совершает квантовый скачок с высшей орбиты на низшую (или, что то же самое, с высшего энергетического уровня на низший), испуская при этом фотон строго определенной частоты, соответствующей разности энергий между двумя энергетическими уровнями. Теперь, если предположить, что электрон в действительности представляет собой микроскопический магнит, а сам атом помещен во внешнее магнитное поле, энергия электрона будет зависеть от полярности его магнитного спина — если магнитное поле электрона на орбите однонаправлено внешнему магнитному полю, он обладает одной энергией, если же оно ориентировано в противоположном направлении, то другой. То есть электроны с противоположным магнитным спином, находящиеся на одной орбитали, будут обладать несколько различающимися энергиями, и каждый энергетический уровень окажется расщеплен на два близких подуровня. Соответственно, там, где раньше имелась единственная возможная энергия квантового перехода между двумя уровнями, теперь имеется четыре возможных энергии перехода. На спектре излучения это должно отразиться таким образом, что вместо одной четко выделенной спектральной линии (частоты излучения) в мощном магнитном поле появятся четыре близко расположенных равноудаленных спектральных линии (частоты).
|
|
|
В атоме водорода электрон находится в силовом поле, которое создается только ядром. В многоэлектронных атомах на каждый электрон действует не только ядро, но все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако. Состояние электронов в сложных атомах ив молекулах определяют путем приближенного решения уравнения Шредингера. Уравнение Шредингера может решаться отдельно для каждого находящего в атоме электрона, состояние которого, как и в атоме водорода, будет определяться значениями квантовых чисел n, l, m и s. Возникновение спектров излучения многоэлектронных атомов обусловлено переходами электронов из одного электронного слоя в другой, расположенный ближе к ядру. Если энергия возбуждения невелика (порядка 10эВ), то возбуждаются только внешние энергетические уровни атома, т.е. имеют место только переходы внешних электронов (из валентного и соседнего слоя) в более далекие электронные слои (не заполненными электронами). Через малый промежуток времени (порядка 10-8 с) эти электроны возвращаются в исходные слои. При этом испускаются небольшие кванты энергии, частоты которых соответствуют оптическому спектру (спектру видимого сета и части инфракрасного и ультрафиолетового излучения). Для того чтобы вызвать перемещение электронов, находящихся во внутренних слоях атома, необходима большая энергия возбуждения, порядка 104-105 эВ. Это обусловлено, во-первых, сильной связью внутренних электронов с ядром, и во-вторых, тем, что внутренние слои целиком заполнены (поэтому внутренние слои можно перевести только на периферию атома). Через малый промежуток времени – порядка 10-8 с – на «вакантное место», освободившееся во внутреннем электроном слое, перейдет электрон из соседнего внутреннего слоя или с периферии атома. Этот процесс сопровождается испускание большого кванта энергии; его частота соответствует рентгеновскому спектру. Квантовое число n, определяющее дискретный ряд энергетических уровней, называют главным числом.
|
|
|
Вынужденное излучение
|
|
|
Для понимания сущности этого явления необходимо рассмотреть элементарные акты взаимодействия электромагнитного излучения с атомной системой. Предположим для простоты, что рассматриваемая нами квантовая система обладает лишь двумя энергетическими уровнями: верхним 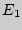 и нижним
и нижним 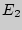 (рис. 1.1). Рассматривая вопрос об излучении энергии абсолютно черным тело, А.Эйнштейн установил, что квантовые переходы атомной системы связаны с тремя процессами: поглощением энергии системой (рис. 1.1a), спонтанным излучением (рис. 1.1б) и вынужденным излучением (рис. 1.1в). Суть процесса индуцированного (вынужденного) излучения заключается в следующем. Внешнее поле обуславливает не только поглощение энергии, но может вызвать и обратный процесс, а именно переход возбужденного атома в основное состояние с излучением кванта энергии. Этот процесс возможен только в средах, атомы которой имеют метастабильные уровни. Время жизни на этих уровнях велико по сравнению с обычным временем жизни возбужденных уровней (
(рис. 1.1). Рассматривая вопрос об излучении энергии абсолютно черным тело, А.Эйнштейн установил, что квантовые переходы атомной системы связаны с тремя процессами: поглощением энергии системой (рис. 1.1a), спонтанным излучением (рис. 1.1б) и вынужденным излучением (рис. 1.1в). Суть процесса индуцированного (вынужденного) излучения заключается в следующем. Внешнее поле обуславливает не только поглощение энергии, но может вызвать и обратный процесс, а именно переход возбужденного атома в основное состояние с излучением кванта энергии. Этот процесс возможен только в средах, атомы которой имеют метастабильные уровни. Время жизни на этих уровнях велико по сравнению с обычным временем жизни возбужденных уровней (  ). Причем процесс при равенстве частоты внешнего поля частоте перехода, будет происходить тем вероятнее, чем ближе фаза внешнего поля к фазе излучаемой энергии. Индуцированное излучение является монохроматическим (или близким к нему). При этом
). Причем процесс при равенстве частоты внешнего поля частоте перехода, будет происходить тем вероятнее, чем ближе фаза внешнего поля к фазе излучаемой энергии. Индуцированное излучение является монохроматическим (или близким к нему). При этом
|
|
|

Рис. 1.1
с увеличением интенсивности поля монохроматичность вынужденного излучения возрастает. Индуцированное излучение совпадает с вызвавшим его излучением не только по частоте, но и по фазе, т.е. оно является когерентным (точнее, обладает высокой степенью когерентности).
А.Эйнштейн ввел понятие об индуцированном излучении при выводе формулы Планка для плотности излучения абсолютно черного тела. Для этого Эйнштейн ввел три коэффициента, характеризующих вероятность осуществления в единицу времени указанных выше процессов, а именно: вероятность спонтанного перехода  , вероятность поглощения
, вероятность поглощения 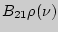 и вероятность вынужденного излучения
и вероятность вынужденного излучения 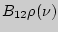 . Две последние величины связаны с наличием внешнего поля, на что указывает множитель
. Две последние величины связаны с наличием внешнего поля, на что указывает множитель 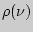 , представляющий собой плотность энергии излучения на частоте
, представляющий собой плотность энергии излучения на частоте  в единичном интервале частот. Здесь
в единичном интервале частот. Здесь 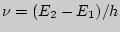 -- частота перехода для рассматриваемой двухуровневой системы. Средние числа переходов в единицу времени соответственно равны
-- частота перехода для рассматриваемой двухуровневой системы. Средние числа переходов в единицу времени соответственно равны 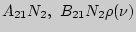 и
и 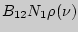 , где
, где  и
и 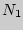 -- число частиц на верхнем и нижнем уровнях.
-- число частиц на верхнем и нижнем уровнях.
Учитывая условия равновесия теплового излучения, то есть условие равенства переходов  и
и  в единицу времени, можно записать:
в единицу времени, можно записать:
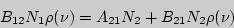
или
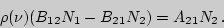
Принимая во внимание распределение частиц по уровням энергии по закону Больцмана:
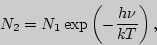
находим
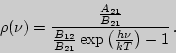
Сравнивая это выражение с формулой Планка для плотности энергии черного излучения:
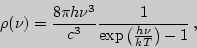
приходим к следующим соотношениям между коэффициентами Эйнштейна
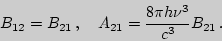
Причем коэффициент  есть величина обратная среднему времени жизни атома в возбужденном состоянии.
есть величина обратная среднему времени жизни атома в возбужденном состоянии.
Рентгеновские спектры
Рентге́новское излуче́ние — электромагнитные волны, энергия фотонов которых лежит на шкале электромагнитных волн между ультрафиолетовым излучением и гамма-излучением (от ~10 эВ до ~1 МэВ), что соответствует длинам волн от ~103 до ~10−2 Å (от ~10−7 до ~10−12 м)
Энергетические диапазоны рентгеновского излучения и гамма-излучения перекрываются в широкой области энергий. Оба типа излучения являются электромагнитным излучением и при одинаковой энергии фотонов — эквивалентны. Терминологическое различие лежит в способе возникновения — рентгеновские лучи испускаются при участии электронов (либо связанных в атомах, либо свободных) в то время как гамма-излучение испускается в процессах девозбуждения атомных ядер. Фотоны характеристического (то есть испускаемого при переходах в электронных оболочках атомов) рентгеновского излучения имеют энергию от 10 эВ до 250 кэВ, что соответствует излучению с частотой от 2·1015 до 6·1019 Гц и длиной волны 0,005—100 нм(общепризнанного определения нижней границы диапазона рентгеновских лучей в шкале длин волн не существует). Мягкое рентгеновское излучение характеризуется наименьшей энергией фотона и частотой излучения (и наибольшей длиной волны), а жёсткое рентгеновское излучение обладает наибольшей энергией фотона и частотой излучения (и наименьшей длиной волны). Жёсткое рентгеновское излучение используется преимущественно в промышленных целях. Условная граница между мягким и жёстким рентгеновским излучением на шкале длин волн находится около 2 Å (≈6 кэВ)[1].
Длина волны рентгеновских лучей сравнима с размерами атомов, поэтому не существует материала, из которого можно было бы изготовить линзу для рентгеновских лучей. Кроме того, при перпендикулярном падении на поверхность рентгеновские лучи почти не отражаются. Несмотря на это, в рентгеновской оптике были найдены способы построения оптических элементов для рентгеновских лучей. В частности, выяснилось, что их хорошо отражает алмаз[4].
Рентгеновские лучи могут проникать сквозь вещество, причём различные вещества по-разному их поглощают. Поглощение рентгеновских лучей является важнейшим их свойством в рентгеновской съёмке. Интенсивность рентгеновских лучей экспоненциально убывает в зависимости от пройденного пути в поглощающем слое (I = I0e-kd, где d — толщина слоя, коэффициент k пропорционален Z³λ³, Z — атомный номер элемента, λ — длина волны).
Молекулярные спектры
Если атомные спектры состоят из отдельных линий, то при наблюдении с низким разрешением молекулярные спектры представляются состоящими из полос. При применении приборов с высокой разрешающей способностью обнаруживается, что полосы состоят из большого числа тесно расположенных линий. В соответствии с их характером спектры молекул носят название полосатых спектров. В зависимости от того, изменение каких видов энергии (электронной, колебательной или вращательной) вызывает испускание молекулой фотона, различают следующие типы полос: 1) вращательные; 2) колебательно-вращательные; 3) электронно-колебательные.
В основном состоянии молекулы все три вида энергии имеют минимальное значение. При сообщении молекуле достаточного количества энергии она переходит в возбужденное состояние и затем, совершая разрешенный правилами отбора переход в одно из более низких энергетических состояний, излучает фотон с энергией
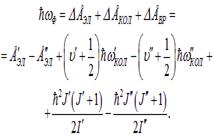
| (8.24) |
Следует отметить, что значения частоты 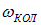 и момента инерции I зависят от электронных конфигураций молекулы и поэтому обозначены одним и двумя штрихами.
и момента инерции I зависят от электронных конфигураций молекулы и поэтому обозначены одним и двумя штрихами.
Учитывая соотношения между энергиями
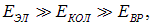
приходим к выводу, что при слабых возбуждениях изменяется только 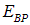 при более сильных —
при более сильных — 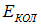 , и лишь при еще более сильных возбуждениях изменяется электронная конфигурация молекулы, то есть
, и лишь при еще более сильных возбуждениях изменяется электронная конфигурация молекулы, то есть 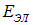 . Соответственно, наименьшей энергией обладают фотоны, связанные с вращательными переходами (электронная конфигурация и энергия колебательного движения не изменяются). Учитывая, что
. Соответственно, наименьшей энергией обладают фотоны, связанные с вращательными переходами (электронная конфигурация и энергия колебательного движения не изменяются). Учитывая, что  , находим
, находим
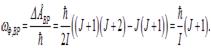
| (8.25) |
Измерение энергии таких фотонов позволяет определить момент инерции молекулы и, следовательно, ее размер 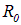 . Например, для НCl найдено
. Например, для НCl найдено 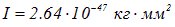 , что соответствует
, что соответствует 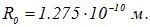
При переходах, сопровождающихся изменениями и колебательного, и вращательного состояний молекулы, частота излучаемого фотона может быть записана в виде
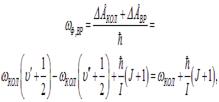
| (8.26) |
где было учтено, что 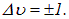
Дата добавления: 2018-06-27; просмотров: 359; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
