Интервальные оценки неизвестных параметров(дляMX)
Опр.Случайные величины 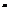 н=
н= 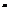 н(
н( 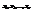 ) и
) и 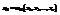 , являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра
, являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра  с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости
с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости 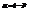 ), если для доверительного интервала вероятность
), если для доверительного интервала вероятность 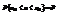 . (1) При этом интервал
. (1) При этом интервал 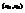 называется двусторонним доверительным интервалом для параметра
называется двусторонним доверительным интервалом для параметра 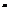 .
.
Замечание 2. В соотношение (1) случайными являются 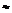 и
и 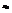 ,
, 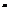 - число. Замечание 3. Пусть
- число. Замечание 3. Пусть  - точечная оценка параметра
- точечная оценка параметра 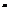 . Если
. Если 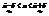 - доверительный интервал. Тогда
- доверительный интервал. Тогда 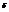 - точность интервальной оценки. Предположим, что
- точность интервальной оценки. Предположим, что 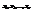 - выборка из нормального распределения генеральной совокупности с параметрами
- выборка из нормального распределения генеральной совокупности с параметрами 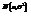 . Построить доверительные интервалы для
. Построить доверительные интервалы для 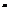 и
и  . Могут возникнуть 4 случая:
. Могут возникнуть 4 случая:
1. Пусть  - известно. Построить ДИ для
- известно. Построить ДИ для 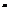 . Этот ДИ нужно строить при помощи точечной оценки
. Этот ДИ нужно строить при помощи точечной оценки 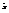 . По следствию из теоремы 1.
. По следствию из теоремы 1. 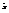 ~N(
~N( 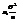 ).По лемме о нормал распред.
).По лемме о нормал распред. 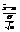 ~N(0,1),
~N(0,1),  .
.
 - функция Лапласа. t – корень уравнения
- функция Лапласа. t – корень уравнения  .
.
Интервальные оценки неизвестных параметров(для DX)
Опр.Случайные величины 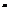 н=
н= 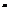 н(
н( 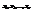 ) и
) и 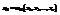 , являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра
, являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра 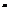 с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости
с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости 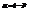 ), если для доверительного интервала вероятность
), если для доверительного интервала вероятность 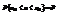 . (1) При этом интервал
. (1) При этом интервал 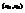 называется двусторонним доверительным интервалом для параметра
называется двусторонним доверительным интервалом для параметра 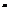 .
.
|
|
|
Замечание 2. В соотношение (1) случайными являются 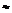 и
и 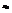 ,
, 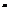 - число. Замечание 3. Пусть
- число. Замечание 3. Пусть  - точечная оценка параметра
- точечная оценка параметра 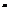 . Если
. Если 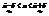 - доверительный интервал. Тогда
- доверительный интервал. Тогда 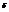 - точность интервальной оценки. Предположим, что
- точность интервальной оценки. Предположим, что 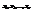 - выборка из нормального распределения генеральной совокупности с параметрами
- выборка из нормального распределения генеральной совокупности с параметрами 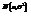 .
.
1.Пусть 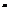 - известно. Построить интервальную оценку для
- известно. Построить интервальную оценку для  .
. 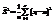 - неисправленная выборочная дисперсия.
- неисправленная выборочная дисперсия. 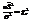 .
.
Проверка статистических гипотез.
Предположим, что x1,…,xn – выборка из генеральной совокупности с функцией распределения F(x). F(x) может быть полностью неизвестна, тогда можно поставить следующую гипотезу:
H0: F(x)=F0(x), где F0(x) – конкретная функция распределения. Если вид функции распределения 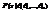 известен с точностью до каких-то m неизвестных параметров. Тогда гипотеза
известен с точностью до каких-то m неизвестных параметров. Тогда гипотеза  - заданные числа. Пусть x1,…,xn - берется из нормальной генеральной совокупности.
- заданные числа. Пусть x1,…,xn - берется из нормальной генеральной совокупности.
Допустим  -известно и оно равно 1, т.е. ГС ~ N(a,1). Тогда
-известно и оно равно 1, т.е. ГС ~ N(a,1). Тогда 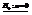 или
или  .
.
Пусть известно a=0, т.е. выборка берется из  .
. 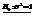 или
или 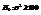 . Пусть a и
. Пусть a и 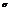 неизвестны:
неизвестны: 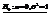 или
или 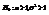 Подчеркнутые гипотезы называются простыми, поскольку задают единственную точку в пространстве параметров. Если гипотеза задает 2 и большее число точек в пространстве, то такая гипотеза называется сложной. H0 – основная или нулевая гипотеза. H1 – конкурирующая гипотеза или альтернативна.
Подчеркнутые гипотезы называются простыми, поскольку задают единственную точку в пространстве параметров. Если гипотеза задает 2 и большее число точек в пространстве, то такая гипотеза называется сложной. H0 – основная или нулевая гипотеза. H1 – конкурирующая гипотеза или альтернативна.
|
|
|
Пусть X- выборочное пространство, т.е. это множество возможных значений вектора 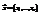 . Для построения критерия проверки гипотезы в выборочном пространстве выбирается критическая область
. Для построения критерия проверки гипотезы в выборочном пространстве выбирается критическая область
Дата добавления: 2018-05-13; просмотров: 214; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
